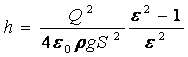¿Con qué fuerza actuarían mutuamente dos cargas puntuales de un culombio, situadas a una distancia de 1 Km. la una de la otra?
Solución:
La fuerza es muy grande. Es imposible transmitir al cuerpo de dimensiones pequeñas una carga de un culombio, puesto que las fuerzas electrostáticas de repulsión son tan grandes que la carga no podrá mantenerse en el cuerpo.
Comparar las fuerzas de atracción gravitatoria y eléctrica entre un electrón y un protón.
Solución:
![]()
![]()
![]()
Supongamos que la fuerza que actúa entre dos cargas puntuales, depende de la distancia según la ley l/r,![]() donde:1)
donde:1)![]() 2)
2)![]() ¿Cómo se portará la carga puntual, metida dentro de una esfera cargada uniformemente? En el momento inicial la carga puntual se encontraba en reposo.
¿Cómo se portará la carga puntual, metida dentro de una esfera cargada uniformemente? En el momento inicial la carga puntual se encontraba en reposo.
Solución:
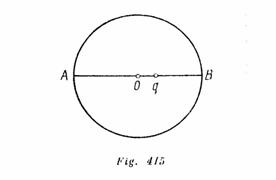
Si las cargas tienen el mismo signo, entonces para ![]() la carga puntual se moverá en dirección al punto 0; para
la carga puntual se moverá en dirección al punto 0; para ![]() en dirección al punto B (fig. 415). Si las cargas tienen signos diferentes la dirección del movimiento será inversa.
en dirección al punto B (fig. 415). Si las cargas tienen signos diferentes la dirección del movimiento será inversa.
Dos esferas pequeñas cargadas igualmente, pero con cargas de signos opuestos, están fijas en un plano horizontal, a cierta distancia a la una de la otra. La tercera esfera cargada está colgada de un hilo. El punto de suspensión una vez se desplaza de tal modo, que esta esfera quede en estado de equilibrio, exactamente sobre la primera esfera fija, a una distancia a de la misma, y la segunda vez, sobre la segunda. Encontrar los ángulos de desviación del hilo con relación a la vertical, sabiendo que sobre la primera esfera el ángulo de desviación es dos veces mayor que éste sobre la segunda esfera.
Solución:
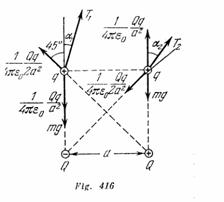
Las condiciones de equilibrio para la esfera colgada están dadas, para ambos casos que estamos analizando, por las ecuaciones.
![]()
![]()
![]()
![]()
donde ![]() y
y ![]() son las tensiones del hilo;
son las tensiones del hilo; ![]() Y
Y ![]() , los ángulos de desviación del hilo; (+Q) Y (-Q), las cargas de las esferas fijas; +q es la carga de la esfera colgada; m, la masa de la esfera suspendida (fig. 416). Excluyendo las incógnitas del sistema de ecuaciones dado, recibimos
, los ángulos de desviación del hilo; (+Q) Y (-Q), las cargas de las esferas fijas; +q es la carga de la esfera colgada; m, la masa de la esfera suspendida (fig. 416). Excluyendo las incógnitas del sistema de ecuaciones dado, recibimos
![]()
de donde obtenemos: ![]()
Por consiguiente,
![]() para
para 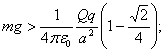
![]() para
para 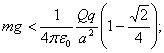
Una carga eléctrica puntual +q se encuentra a la distancia d de una lámina conductora grande. ¿Con qué fuerza actúa la lámina sobre la carga?
Solución:
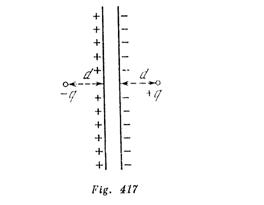
Las cargas negativas inducidas en la superficie del conductor se distribuyen de modo que la intensidad resultante del campo dentro del conductor, creado por una carga puntual positiva y por las cargas negativas inducidas, es igual a cero. (Las cargas positivas inducidas se dirigirán hacia los bordes alejados de la lámina y podemos prescindir de su campo). Esta distribución de las cargas inducidas no depende del grosor de la lámina. Coloquemos a la izquierda de la lamina, a la misma distancia d, una carga (-q). Es lógico que en la parte izquierda de la lámina las cargas positivas inducidas se distribuyen del mismo modo que las cargas negativas en la parte derecha de la lámina.
Como ponemos a la izquierda de la lamina una carga (-q), el campo eléctrico a la derecha de la lamina no cambiara. De este modo el campo eléctrico creado por la carga (+q) y las cargas inducidas negativas a la derecha de la lamina, coincide con el campo creado por las cargas (+q) y (-q) y por las cargas inducidas en las superficies de la lamina (fig. 417). Si el grosor de la lámina es muy pequeño con relación a d, podremos considerar la lámina infinitamente fina y en este caso el campo creado por las cargas inducidas fuera de la lámina no existe. De esta manera demostramos que el campo a la derecha de la lamina, creado por la carga (+q) y por las cargas negativas inducidas, coincide con el campo creado por las cargas puntuales (+q) y (-q). Como en el punto de la situación de la carga +q la intensidad del campo de las cargas negativas inducidas es igual a la intensidad del campo de la carga puntual –q, que se encuentra a una distancia 2d de +q, entonces la fuerza de atracción que buscamos será igual a
![]()
Dos cargas +Q están fijas y situadas a una distancia a la una de la otra. A lo largo del eje de simetría del sistema de estas cargas puede desplazarse una tercera carga -q que posee una masa m. Considerando pequeña la distancia desde la carga -q hasta la recta que une las cargas +Q, determinar el período de oscilaciones de la carga -q.
Solución:
![]()
Un anillo de alambre fino, de radio R, es portador de una carga eléctrica q. En el centro del anillo se encuentra otra carga ![]() son cargas del mismo signo), siendo
son cargas del mismo signo), siendo ![]() Determinar la fuerza con que el anillo se ensancha.
Determinar la fuerza con que el anillo se ensancha.
Solución:
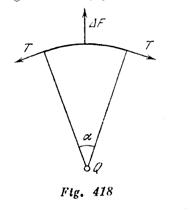
Si ![]() entonces se puede prescindir de la interacción entre los sectores aislados del anillo. Destaquemos un sector pequeño del anillo de longitud R
entonces se puede prescindir de la interacción entre los sectores aislados del anillo. Destaquemos un sector pequeño del anillo de longitud R![]() (fig. 418). Por parte de la carga Q.
(fig. 418). Por parte de la carga Q.
Actúa sobre éste la fuerza
![]() donde
donde ![]()
Las fuerzas de tensión del anillo T equilibran a ![]() F. De la condición de equilibrio y considerando
F. De la condición de equilibrio y considerando ![]() pequeño, podemos escribir
pequeño, podemos escribir
![]() F=2Tsen (T.
F=2Tsen (T.![]() T
T![]()
La fuerza incógnita es la fuerza de tensión ![]()
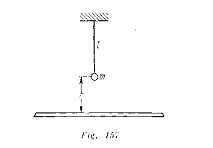
Un cuerpo de masa m está colgado de un hilo de longitud l (fig. 157). A una distancia h debajo del mismo, se encuentra una lámina metálica infinita. El cuerpo posee carga q. Hallar el período de oscilaciones libres de este cuerpo.
Solución:
Cuando el hilo se inclina bajo un ángulo ![]() , sobre la carga q actúa una fuerza F perpendicular a la lámina e igual a
, sobre la carga q actúa una fuerza F perpendicular a la lámina e igual a
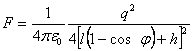
(Véase la solución del problema 413). Para pequeños ángulos de desviación tenemos que ![]() y por lo tanto,
y por lo tanto,![]() En este caso el periodo de oscilaciones será
En este caso el periodo de oscilaciones será
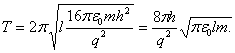
Determinar el período de las pequeñas oscilaciones de una molécula polar en un campo eléctrico homogéneo, cuya intensidad es![]() La molécula polar puede ser representada esquemáticamente como unas «pesas» de longitud
La molécula polar puede ser representada esquemáticamente como unas «pesas» de longitud ![]() , en cuyos extremos se encuentran masas puntuales iguales a
, en cuyos extremos se encuentran masas puntuales iguales a![]() portadores de cargas +q y -q respectivamente
portadores de cargas +q y -q respectivamente ![]() culombios).
culombios).
Solución:
El problema formalmente se reduce a la determinación del periodo de las pequeñas oscilaciones de un péndulo simple de longitud ![]() junto a la posición de equilibrio en el campo de la fuerza
junto a la posición de equilibrio en el campo de la fuerza ![]()
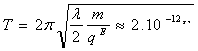
Tres cargas positivas iguales a q están situadas en los vértices de un triángulo equilátero. Los lados del triángulo son iguales a a. Encontrar la intensidad del campo en el vértice de un triángulo regular que tiene como base este triángulo.
Solución:
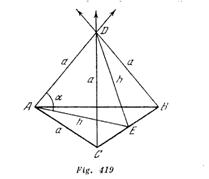
Cada carga crea en el punto D un campo de intensidad ![]() La intensidad resultante será la suma de los tres vectores (fig. 419). La suma de los componentes horizontales de estos vectores es nula, puesto que ellas son iguales en valor y forman la una con los otros ángulos iguales a 120º. Los propios vectores forman con la vertical ángulos
La intensidad resultante será la suma de los tres vectores (fig. 419). La suma de los componentes horizontales de estos vectores es nula, puesto que ellas son iguales en valor y forman la una con los otros ángulos iguales a 120º. Los propios vectores forman con la vertical ángulos ![]() donde
donde ![]() es el ángulo entre la arista del tetraedro y la altura
es el ángulo entre la arista del tetraedro y la altura ![]() del triángulo ABC. Las componentes verticales son iguales entre si y cada una es
del triángulo ABC. Las componentes verticales son iguales entre si y cada una es![]() Del ADE se ve claramente que
Del ADE se ve claramente que![]() de donde la intensidad del campo que buscamos es
de donde la intensidad del campo que buscamos es
![]()
Dos cargas puntuales q1 y q2 se encuentran a una distancia d la una de la otra. Hallar la intensidad del campo eléctrico en el punto que se encuentra a una distancia r1 de la carga q1 y a una distancia r2 de q2. Examinar los casos de cargas del mismo signo y del signo contrario.
Solución:
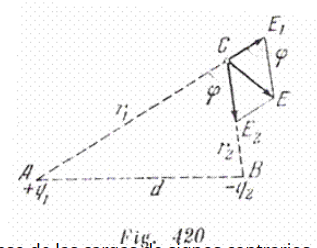
Analicemos el caso de las cargas de signos contrarios, es decir, q>0, q<0. Las intensidades creadas por las cargas q y q son iguales a E1= ![]() y E2=
y E2=![]() , respectivamente. Como vemos en la fig. 420,
, respectivamente. Como vemos en la fig. 420,
![]() =
= ![]() cos
cos![]() . Del
. Del ![]() resulta cos
resulta cos![]() =
=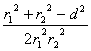 . Por consiguiente,
. Por consiguiente,
E=![]()
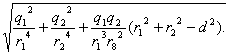
Si las cargas tienen el mismo signo, entonces
E=![]()
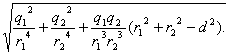
Encontrar la intensidad del campo de un dipolo eléctrico con el momento igual a p = ql en el punto que está a una distancia igual a r (r >1) del eje del dipolo, en dos casos:
1) El punto permanece en una recta que pasa por el eje del dipolo; 2) el punto se halla en una recta perpendicular al eje del dipolo.
Observación. En el caso más simple, el dipolo eléctrico consta de dos cargas iguales, pero de signos contrarios (+q y –q). Una característica importante del dipolo es el momento eléctrico p = ql. El momento eléctrico de un dipolo es un vector dirigido de la carga negativa a la positiva y numéricamente igual a p = ql, donde es la distancia entre las cargas que forman el dipolo.
Solución:
![]()
1)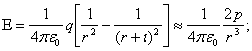
2)![]()
Una carga positiva Q está distribuida uniformemente por un anillo de alambre fino de radio R.Encontrar la intensidad del campo eléctrico en el eje del anillo en función de la distancia r del centro del anillo.
Solución:
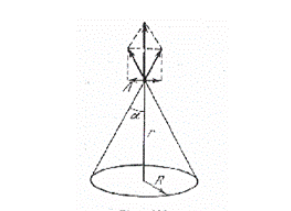
La intensidad del campo E en el punto cualquiera A en el eje del anillo puede hallarse como la suma geométrica de las intensidades creadas por pequeños elementos aislados del anillo cargado (fig. 422). Al sumar los vectores de la intensidad en el punto A, es necesario tener en cuenta solamente las componentes dirigidas a lo largo del eje del anillo. Las componentes de los vectores de la intensidad dirigidas perpendicularmente al eje, tendrán en la suma la resultante nula debido a la simetría. Por lo tanto, la intensidad del campo en el punto A es
![]()
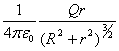 .
.
Un anillo de alambre fino de radio![]() posee cierta carga eléctrica igual a
posee cierta carga eléctrica igual a ![]() . ¿Cómo se moverá un cuerpo puntual de masa
. ¿Cómo se moverá un cuerpo puntual de masa ![]() que posee una carga igual a
que posee una carga igual a ![]() , si en el momento inicial ésta estaba en reposo en un punto sobre el eje del anillo, a una distancia
, si en el momento inicial ésta estaba en reposo en un punto sobre el eje del anillo, a una distancia ![]() de un centro? El anillo esta fijo.
de un centro? El anillo esta fijo.
Solución:
La fuerza que actúa sobre la carga ![]() es
es
![]()
Y estará siempre dirigida al centro del anillo; como ![]() , entonces, despreciando x en el denominador en comparación con R, obtenemos que
, entonces, despreciando x en el denominador en comparación con R, obtenemos que
![]()
De este modo la fuerza es proporcional a x y está dirigida al centro del anillo. Bajo la influencia de esta fuerza, la carga realiza un movimiento oscilatorio, cuyo período es
![]()
Tomando en consideración las condiciones de la dimensión, encontrar (claro está que con precisión hasta un coeficiente numérico) la intensidad de un campo eléctrico creada; 1) por una lamina infinitamente extendida, cargada con densidad superficial ![]() ; 2) por un hilo infinitamente largo, cargado con densidad lineal
; 2) por un hilo infinitamente largo, cargado con densidad lineal ![]() .
.
Solución:
En ambos casos la intensidad del campo eléctrico en un punto alejado en r de la lamina o del hilo, puede depender solo de ![]() ó
ó ![]() y r . La dependencia de
y r . La dependencia de ![]() y
y ![]() deberá ser lineal (principio de superposición), o sea,
deberá ser lineal (principio de superposición), o sea,![]() , donde
, donde ![]() , donde
, donde ![]() y
y ![]() son funciones por ahora desconocidas de r .
son funciones por ahora desconocidas de r .
Observación. El principio de la superposición en este caso consiste en que la intensidad de la suma de las cargas es igual a la suma de las intensidades creadas por cada carga por separado.
Como sabemos,![]() . Las dimensiones de
. Las dimensiones de ![]() y
y ![]() son:
son: ![]() y
y ![]() . Es evidente que en el caso de lamina
. Es evidente que en el caso de lamina ![]() y en el caso del hilo
y en el caso del hilo ![]() , donde
, donde ![]() y
y ![]() son cualesquier coeficientes adimensionales. Basándose en los conceptos de simetría hallamos fácilmente la dirección de la intensidad. La intensidad E esta dirigida perpendicularmente a la lámina o al hilo. Teóricamente hallamos los coeficientes
son cualesquier coeficientes adimensionales. Basándose en los conceptos de simetría hallamos fácilmente la dirección de la intensidad. La intensidad E esta dirigida perpendicularmente a la lámina o al hilo. Teóricamente hallamos los coeficientes ![]() y
y ![]() , cuyos valores son
, cuyos valores son ![]() y
y ![]() .
.
Una lámina metálica rectangular, de lados iguales a ![]() y
y ![]() , posee una carga
, posee una carga ![]() .El grosor de la lámina
.El grosor de la lámina ![]() es mucho menor que
es mucho menor que ![]() y
y ![]() . Determinar la intensidad del campo, creada por esta lámina cargada, en los puntos del espacio próximos al centro de la misma.
. Determinar la intensidad del campo, creada por esta lámina cargada, en los puntos del espacio próximos al centro de la misma.
Solución:
Debido al pequeño grosor de la lámina podemos considerar que la carga está distribuida uniformemente en ambas superficies, cuyas áreas son iguales a ab. De este modo, la densidad superficial de la carga es ![]() =
=![]() ab. El campo dentro del metal será nulo y fuera del metal su intensidad será
ab. El campo dentro del metal será nulo y fuera del metal su intensidad será
![]()
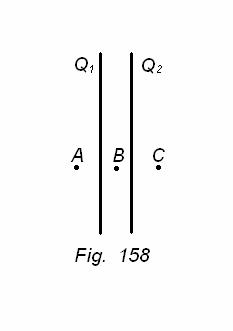
Dos lámina metálicas paralelas, cuyas áreas son iguales a S, tienen cargas ![]() y respectivamente.
y respectivamente.
La distancia entre las láminas es mucho menor que sus dimensiones lineales. Determinar la intensidad del campo eléctrico en los puntos A, B y C.
Solución:
![]()
![]()
![]()
La intensidad será positiva si está dirigida desde la izquierda hacia la derecha.
Cuál será la intensidad del campo eléctrico en la superficie de un conductor, si la densidad de la carga superficial es ![]() ?
?
Solución:
Separemos en el conductor un pequeño segmento AB de modo que podemos considerarlo plano (fig. 423). En las cercanías de este segmento el campo puedo analizarse como la superposición de dos campos: del campo creado por las cargas de este segmento (vectores E1, ![]() ) y del campo creado por las demás cargas del conductor (vectores E2, E´2). Como el segmento AB puede considerarse plano, entonces E1 = E’1 =
) y del campo creado por las demás cargas del conductor (vectores E2, E´2). Como el segmento AB puede considerarse plano, entonces E1 = E’1 =![]() . Además, como el campo creado por las cargas que se encuentran fuera de los límites del segmento AB, es continuo, entonces E2 = E´2. Al final, como dentro del conductor no existe campo, entonces E’1 = E´2 de donde, teniendo en cuenta las igualdades anteriores, obtenemos
. Además, como el campo creado por las cargas que se encuentran fuera de los límites del segmento AB, es continuo, entonces E2 = E´2. Al final, como dentro del conductor no existe campo, entonces E’1 = E´2 de donde, teniendo en cuenta las igualdades anteriores, obtenemos
E1 = E2 = ![]() .Por lo tanto, la intensidad incógnita será
.Por lo tanto, la intensidad incógnita será
E = E1 + E2 =![]() +
+![]() =
= ![]()
Todo el espacio entre dos láminas paralelas infinitas está ocupada por una carga de densidad volumétrica constante igual a ![]() . La distancia entre las láminas es a. Encontrar la dependencia de la intensidad del campo eléctrico en función de la distancia considerada a partir del centro de las láminas.
. La distancia entre las láminas es a. Encontrar la dependencia de la intensidad del campo eléctrico en función de la distancia considerada a partir del centro de las láminas.
Solución:
Si ![]()
![]()
![]() , entonces E =
, entonces E = ![]() . Si
. Si![]() >
> ![]() , entonces E =
, entonces E = ![]() .
.
Dentro de una esfera de radio![]() existe una carga volumétrica, con densidad constante igual a
existe una carga volumétrica, con densidad constante igual a ![]() . Hallar la dependencia de la intensidad del campo eléctrico respecto a la distancia hasta el centro de la esfera.
. Hallar la dependencia de la intensidad del campo eléctrico respecto a la distancia hasta el centro de la esfera.
Solución:
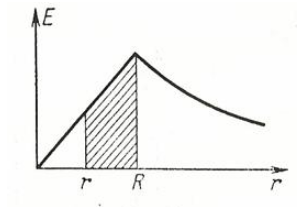
Determinemos la intensidad del campo a una distancia r
![]()
Fuera de la esfera ![]() la intensidad será
la intensidad será
![]()
Donde es la carga de la esfera. (El grafico ![]() véase en la fig. 424).
véase en la fig. 424).
Hallar la intensidad del campo eléctrico dentro y fuera de un cilindro infinitamente largo, cargado con densidad volumétrica igual a ![]() . El radio del cilindro es R.
. El radio del cilindro es R.
Solución:
Determinemos la intensidad del campo a una distancia ![]() del eje del cilindro. Las cargas que se encuentran dentro del cilindro de radio r crean a una distancia r del eje del cilindro la misma intensidad que crearan si estuvieran en el eje. Las cargas que se encuentran fuera del cilindro no crean campo.
del eje del cilindro. Las cargas que se encuentran dentro del cilindro de radio r crean a una distancia r del eje del cilindro la misma intensidad que crearan si estuvieran en el eje. Las cargas que se encuentran fuera del cilindro no crean campo.
Por lo tanto, si ![]() , entonces
, entonces
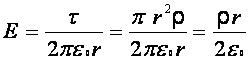
Si ![]() , resulta que
, resulta que
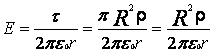
Dentro de una esfera cargada con densidad volumétrica constante ![]() , hay una cavidad esférica. La distancia entre el centro de la esfera y el centro de la cavidad es igual a
, hay una cavidad esférica. La distancia entre el centro de la esfera y el centro de la cavidad es igual a ![]() . Demostrar que la intensidad E del campo eléctrico dentro de la cavidad es igual a
. Demostrar que la intensidad E del campo eléctrico dentro de la cavidad es igual a ![]() y esta dirigida a lo largo de la recta que une los centros de las esferas.
y esta dirigida a lo largo de la recta que une los centros de las esferas.
Solución:
![]()
(Véase la figura 425 y la resolución del problema 428).
Dentro de un cilindro cargado con densidad volumétrica constante![]() , hay una cavidad cilíndrica. La distancia entre los ejes del cilindro y de la cavidad es igual a . Demostrar que la intensidad E del campo eléctrico dentro de la cavidad es igual a
, hay una cavidad cilíndrica. La distancia entre los ejes del cilindro y de la cavidad es igual a . Demostrar que la intensidad E del campo eléctrico dentro de la cavidad es igual a ![]() y esta dirigida paralelamente a la perpendicular que une los ejes.
y esta dirigida paralelamente a la perpendicular que une los ejes.
Solución:
Véanse las resoluciones de los problemas 430 y 429
Una molécula se encuentra a una distancia r del eje de un cilindro metálico infinitamente largo. El cilindro esta cargado uniformemente; la carga que cae en una unidad de su longitud, es igual a ![]() . La molécula tiene la forma de unas «pesas» de longitud
. La molécula tiene la forma de unas «pesas» de longitud ![]() , en los extremos de las cuales se hallan cargas. Determinar la fuerza que actúa sobre la molécula.
, en los extremos de las cuales se hallan cargas. Determinar la fuerza que actúa sobre la molécula.
Solución:
La molécula se atraerá por el cilindro cargado, la fuerza de atracción es.
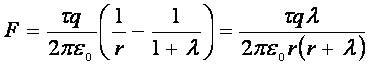
En esta expresión nosotros podemos prescindir del valor ![]() en comparación con r(r no puede ser menor que el radio del cilindro). Por fin, para F recibimos la expresión:
en comparación con r(r no puede ser menor que el radio del cilindro). Por fin, para F recibimos la expresión:
![]()

A cierta distancia del eje de un cilindro uniformemente cargado se encuentran dos moléculas de igual masa. Una molécula tiene el momento eléctrico constante![]() (véase el problema 420). La distancia entre las cargas de la otra molécula se determina por la relación
(véase el problema 420). La distancia entre las cargas de la otra molécula se determina por la relación ![]() donde
donde ![]() es la intensidad media del campo que actúa sobre la molécula, y
es la intensidad media del campo que actúa sobre la molécula, y ![]() , un coeficiente constante. En el momento inicial los momentos eléctricos de las moléculas son iguales y las velocidades de las mismas son nulas. ¿Cuál de las moléculas, bajo la acción de la fuerza de atracción, alcanzará más rápido la superficie del cilindro?
, un coeficiente constante. En el momento inicial los momentos eléctricos de las moléculas son iguales y las velocidades de las mismas son nulas. ¿Cuál de las moléculas, bajo la acción de la fuerza de atracción, alcanzará más rápido la superficie del cilindro?
Solución:
Primeramente las fuerzas que actúan sobre ambas moléculas son iguales. Al aproximarse al cilindro, la fuerza ![]() que actúa sobre la molécula con un momento eléctrico constante crece proporcionalmente a
que actúa sobre la molécula con un momento eléctrico constante crece proporcionalmente a ![]() (véase el problema 432). La fuerza
(véase el problema 432). La fuerza ![]() que actúa sobre la molécula «elástica», crece con mas rapidez proporcionalmente a (a cuenta del aumento continuo del momento eléctrico de esta molécula).
que actúa sobre la molécula «elástica», crece con mas rapidez proporcionalmente a (a cuenta del aumento continuo del momento eléctrico de esta molécula).
Las masas de las moléculas son iguales y por eso la aceleración de la segunda molécula al aproximarse al cilindro, aumentara con mayor rapidez que de la primera y ella alcanzará más rápido la superficie del cilindro.
Una lamina metálica rectangular con los lados ![]() y
y ![]() , tiene carga
, tiene carga ![]() . El grosor de la lamina
. El grosor de la lamina ![]() es mucho menor que los lados
es mucho menor que los lados ![]() y
y ![]() . Una carga puntual
. Una carga puntual ![]() se aproxima a una distancia
se aproxima a una distancia ![]() del centro de la lámina. La distancia
del centro de la lámina. La distancia ![]() es mucho menor que los lados de la lamina. Determinar la fuerza con que la lamina actúa sobre la carga
es mucho menor que los lados de la lamina. Determinar la fuerza con que la lamina actúa sobre la carga ![]() . ¿En qué caso la lamina cargada positivamente atraerá una carga positiva?
. ¿En qué caso la lamina cargada positivamente atraerá una carga positiva?
Solución:
Teniendo en cuenta que ![]() y
y ![]() son mucho más grandes que c y d podemos representar la lámina infinitamente grande.
son mucho más grandes que c y d podemos representar la lámina infinitamente grande.
Considerando que la intensidad del campo de algunas cargas es igual a la suma de las intensidades creadas por cada una de estas cargas y utilizando las soluciones de los problemas 413 y 424, recibimos el valor de la fuerza incógnita:
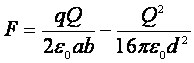
El primer sumando corresponde a la fuerza de repulsión, el segundo, a la fuerza de atracción. La lámina cargada positivamente atraerá una carga puntual positiva, si
![]() Osea, si
Osea, si ![]() .
.
Dentro de una esfera de radio ![]() hay una carga volumétrica de densidad constante
hay una carga volumétrica de densidad constante ![]() . Encontrar la dependencia del potencial en función de la distancia del centro de la esfera.
. Encontrar la dependencia del potencial en función de la distancia del centro de la esfera.
Solución:
Fuera de la esfera el potencial es ![]() . Para determinar el potencial dentro de la esfera (siendo r<R) hace falta adicionar al potencial
. Para determinar el potencial dentro de la esfera (siendo r<R) hace falta adicionar al potencial ![]() un valor numéricamente igual al trabajo realizado por el campo sobre una carga unitaria positiva durante su desplazamiento radial desde r hastaR . Este trabajo es igual al área sombreada en la fig. 424 (véase el problema 428).
un valor numéricamente igual al trabajo realizado por el campo sobre una carga unitaria positiva durante su desplazamiento radial desde r hastaR . Este trabajo es igual al área sombreada en la fig. 424 (véase el problema 428).
Calculando, obtenemos que ![]()
A una distancia ![]() de una carga puntual
de una carga puntual![]() se encuentra el centro de una esfera conductora sin carga de radio R. ¿Que valor tendrá el potencial de la esfera?
se encuentra el centro de una esfera conductora sin carga de radio R. ¿Que valor tendrá el potencial de la esfera?
Solución:
Todos los puntos de la esfera tienen el mismo potencial. Para resolver el problema es suficiente hallar el potencial de un punto. Es más cómodo determinar el potencial del centro de la esfera que es igual al potencial creado en el centro de la esfera por una carga puntual ![]() más el potencial creado por las cargas que surgen en la superficie de la esfera debido a la inducción electrostática. Pero este último potencial es nulo, puesto que la carga resultante en la esfera es nula y todos los elementos de la carga se encuentran a igual distancia del centro. Por consiguiente, el potencial de la esfera es
más el potencial creado por las cargas que surgen en la superficie de la esfera debido a la inducción electrostática. Pero este último potencial es nulo, puesto que la carga resultante en la esfera es nula y todos los elementos de la carga se encuentran a igual distancia del centro. Por consiguiente, el potencial de la esfera es ![]() .
.
A distancia ![]() de la carga puntual
de la carga puntual ![]() se halla una esfera conductora de radio r, unida por un alambre fino y largo con la tierra. Determinar la magnitud de la carga negativa inducida a la esfera. Puede prescindirse de la influencia del alambre.
se halla una esfera conductora de radio r, unida por un alambre fino y largo con la tierra. Determinar la magnitud de la carga negativa inducida a la esfera. Puede prescindirse de la influencia del alambre.
Solución:
El potencial de la esfera ![]() es igual a
es igual a
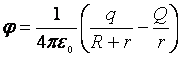
Como la esfera esta puesta a tierra, su potencial es nulo, es decir:
![]() . Por lo tanto
. Por lo tanto![]() ,
,
Un electrón se mueve dentro de un tubo metálico de sección transversal variable (fig. 159).
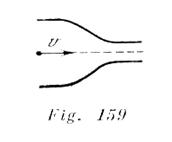
¿Cómo cambiará la velocidad del electrón al aproximarse a la parte mas estrecha del tubo?
Solución:
En la parte más estrecha del tubo surgirán cargas inducidas positivas. Bajo la acción de estas cargas, el electrón comenzará a acelerarse. La energía cinética del electrón aumentará debido a la disminución de la energía potencial del sistema electrón — tubo.
Dos esferas metálicas concéntricas sin cargas, cuyos radios son R1 y R3, además R1 < R3, están unidas por alambre fino. El alambre pasas por un pequeño orificio de la esfera, situada concentricamente entre las dos primeras. Esta esfera tiene radio R2 y posee carga +Q distribuida uniformemente por ella. Despreciando la influencia del alambre de unión, determinar la carga inducida en la esfera metálica interna. Solución:
![]()
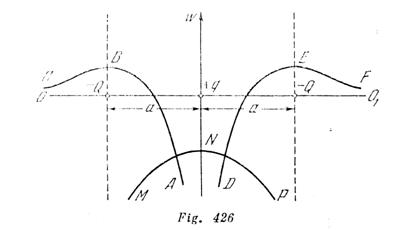
En una recta se encuentran tres cargas: una positiva +q y dos negativas –Q. ¿Para qué relación de valores de las cargas estas últimas estarán en equilibrio? ¿Será este equilibrio estable? Representar gráficamente la dependencia entre la energía potencial de cada carga y su posición en la recta, considerando fijas las otras dos cargas.
Solución:
Para el equilibrio de la carga q hace falta que las cargas (-Q) se encuentren a iguales distancias a de ella (fig. 426). La suma de las fuerzas que actúan sobre la carga (-Q) también es nula:
![]()
De ahí q=Q/4. La distancia a puede ser cualquiera. El equilibrio es inestable, puesto que durante el movimiento de la carga –Q a lo largo de OO’ en el segmento x de la carga q, la fuerza de atracción ![]() que actúa por parte de la carga q es menor que la fuerza de repulsión:
que actúa por parte de la carga q es menor que la fuerza de repulsión: ![]() y la carga (-Q) irá aún más lejos de la posición de equilibrio. Al desplazarse la carga –Q a lo largo de OO1 a la distancia x en dirección de la carga q, Eq>FQ para x≤a y el sistema no vuelve a la posición de equilibrio. El equilibrio también se perturba, como se ve fácilmente,
y la carga (-Q) irá aún más lejos de la posición de equilibrio. Al desplazarse la carga –Q a lo largo de OO1 a la distancia x en dirección de la carga q, Eq>FQ para x≤a y el sistema no vuelve a la posición de equilibrio. El equilibrio también se perturba, como se ve fácilmente,
por el desplazamiento de la carga q.
La energía potencial de la carga –Q en el campo de otra s dos cargas es
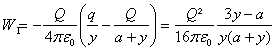 ,
,
donde y es la distancia entre la carga q y una de las cargas –Q. La dependencia de W1 con relación a y, siendo 0≤ y≤∞, se da por la curva ABC para una carga por la curva DEF para otra (fig.426).
La energía de la carga q, estando las cargas –Q inmóviles, es
![]()
donde z es el desplazamiento de la carga q de la posición de equilibrio. Al variar z desde 0 hasta a, la energía cambia de acuerdo con la curva MNP (fig.426).
Es característico que los máximos de todas las tres curvas potenciales corresponden a la posición de las cargas en equilibrio. Precisamente con esto esta relacionado la inestabilidad del equilibrio.
¿Podrá una carga eléctrica en un campo electroestático encontrarse en un estado de equilibrio estable?
Solución:
No, no se podrá. A fin que una carga positiva se encuentre en estado de equilibrio estable es preciso que en el desplazamiento la carga en dirección cualquiera, actúe sobre ésta una fuerza con que la carga vuelva a estado de equilibrio. Por consiguiente, las líneas de fuerza del campo eléctrico se convergerán en el punto donde está situada la carga. Pero las líneas de fuerza del campo eléctrico comienzan en las cargas positivas y terminan en las cargas negativas. En el punto donde se encuentran la carga que analizamos, no existen cargas negativas y por lo tanto, las líneas de fuerza del campo exterior respecto a la carga del campo no pueden convergerse en el punto donde ella se encuentra.
Una esfera conductora, aislada, de radio R, posee una carga +Q. ¿Qué energía tiene la esfera?
Solución:
La energía de la esfera cargada es igual al trabajo que pueden realizar las cargas que se encuentran en la esfera, si ellas abandonan la esfera alejándose infinitamente. Supongamos que de la esfera cada vez se aparte al infinito una porción de carga de q unidades (q<
El trabajo realizado en el desplazamiento de N porciones de, donde N=Q/q es
![]() .
.
Siendo N→∞ (q→0) A=Q²/8πεR. Por lo tanto la energía de la esfera cargada es W=Q²/8πεR. (Esta energía se denomina energía propia.) El mismo resultado puede obtenerse utilizando el grafico de variación del potencial de la esfera con la disminución de la carga. El grafico tendrá la forma de una línea recta que forma un ángulo cualquier con el eje de las abscisas y el trabajo será numéricamente igual al área limitada por el grafico de las coordenadas.
La energía de todo el sistema de cargas es igual a la suma de las energías propias de las cargas que se encuentran en la primera esfera (W= Q/8πεR) y en la segunda esfera (W= Q/8πεR), así como de la energía de interacción de las cargas de la primera esfera con las cargas de la segunda. La energía la energía de interacción es igual al producto de la carga Q por el potencial creado en la superficie de la esfera de radio R por la carga Q. De este modo, la energía incógnita W de todo el sistema es
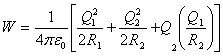 .
.
En el caso, cuando Q=-Q=Q (condensador esférico), tenemos
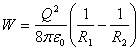 .
.
Existen n esferas metálicas, concéntricas y finas, cuyos radios en orden creciente son iguales a r1, r2 , …, rx. Estas esferas cargas q1, q2, …, qx, respectivamente. Determinar la energía del dado sistema de cargas.
Solución:
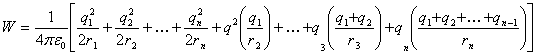
Las placas de un condensador plano de capacidad C están a una distancia l la una de la otra y poseen cargas +Q y -Q respectivamente. Un electro entro en el medio del condensador con velocidad v0, dirigida paralelamente a las placas. ¿Cuál será la velocidad del electrón a una distancia suficientemente grande del condensador? ¿Cuál es el carácter de la variación de la velocidad del electrón (por el valor absoluto) al moverse dentro y fuera del condensador? Examinar los casos, cuando el electrón se encuentra en el momento inicial: 1) a la misma distancia de las placas del condensador; 2) a una distancia igual a l/4 de la placa positiva; 3) a una distancia l/4 de la placa negativa.
Solución:
Como siempre consideramos el potencial en el infinito igual a cero. Entonces los potenciales de las láminas serán iguales respectivamente, a +U/2 y -U/2, siendo U=Q/C. Los potenciales en los puntos de la posición inicial del electrón son iguales, respectivamente, a 0, +U/4, -U/4. Los valores iniciales de la energía total del electrón son
1) ![]()
2)![]()
3)![]() .
.
Las velocidades finales v, v, v se hallan, aplicando el principio de conservación de la energía:
1) ![]() , v=v;
, v=v;
2) ![]() ,
, ![]() ;
;
3)![]() ,
, ![]() .
.
En el primer caso, la velocidad final es igual a la velocidad inicial, en segundo caso, es menor que la velocidad inicial y en el tercer caso, es mayor que la inicial. En todos los casos, la velocidad primero aumenta (durante el movimiento dentro del condensador) y después comienza a disminuir.
Dos cargas puntuales del mismo signo q1 y q2 y masas iguales a m1 y m2 se mueven la una en dirección a la otra. En el momento, cuando la distancia entre las cargas es igual a r1, ellas tienen velocidades iguales a v1 y v2. ¿A que distancia mínima r2 se aproximarán las cargas?
Solución:
La distancia entre las cargas se hará mínima en el momento cuando sus velocidades se hacen iguales, es decir, en momento cuando la velocidad relativa de la cargas es nula. Es evidente que la velocidad de las cargas a distancia mínima entre ellas, de acuerdo con el principio de la conservación del impulso, es igual a ![]() . Valiéndose del principio de la conservación de la energía, podemos escribir que
. Valiéndose del principio de la conservación de la energía, podemos escribir que
![]() ,
,
y hallamos la distancia mínima rentre las cargas
 .
.
Una carga puntual +q se mueve del infinito en dirección a un lamina metálica. Determinar la energía de interacción de la carga y lámina y, también, la velocidad de la carga en el momento, cuando ésta se encuentra a una distancia d de la lámina. Al hallarse a una distancia infinitamente grande de la lámina, la carga tenia velocidad nula.
Solución:
La energía de interacción es igual a la mitad de la energía de interacción de dos cargas puntuales +q y –q, que se encuentra a una distancia 2d, o sea,
![]() .
.
La velocidad se halla de principio de la conservación de la energía. Cuando la carga se encuentra a una distancia infinitamente grande de la lámina, su velocidad es nula y la energía de interacción W también es nula. De este modo, tenemos
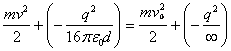 ,
,
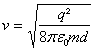 .
.
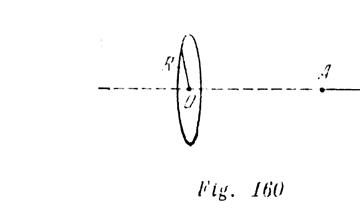
Por un anillo fino de radio R esta distribuida la carga +q. Determinar la velocidad de una carga negativa puntual (-q) en el momento, en que la misma pasa por el centro del anillo, si la carga -q inicialmente se encontraba en reposo suficientemente alejada del anillo, en el punto A del eje (fig. 160). La masa de la carga -q es igual a m. El anillo esta fijo.
Solución:
El trabajo para el movimiento de la carga –q es proporcional a la diferencia de potencial entre el punto O y el punto A que se encuentra en el eje del anillo a una distancia muy grande (fig. 160). El potencial en el infinito es nulo.
El potencial del punto A, si la distancia OA>>R, podremos considerar igual a cero. El potencial en el punto O se halla por la suma de los potenciales creados por pequeñas secciones parciales del anillo:
![]() .
.
Utilizando el principio de conservación de la energía![]() , hallamos que
, hallamos que![]() .
.
Una carga positiva +Q esta distribuida uniformemente por un anillo de alambre fino de radio R. En el centro del anillo se encuentra una carga puntual -q de masa igual a m. A la carga se da una velocidad inicial v a lo largo del eje del anillo.Determinar el carácter del movimiento de la carga en función de la magnitud de la velocidad inicial. El anillo está fijo.
Solución:
La energía total de la carga es ![]() Si
Si ![]() la carga se alejara hacia el infinito. Si W=0, la velocidad de la carga, a un distancia infinitamente grande del centro del anillo, será nula y si W > 0 ella será diferente de cero. Si W < 0, entonces la carga realizará un movimiento periódico a lo largo del eje anillo. La mayor distancia , a la que podrá desplazarse la carga del centro del anillo, puede hallarse basándose en el principio de conservación de la energía
la carga se alejara hacia el infinito. Si W=0, la velocidad de la carga, a un distancia infinitamente grande del centro del anillo, será nula y si W > 0 ella será diferente de cero. Si W < 0, entonces la carga realizará un movimiento periódico a lo largo del eje anillo. La mayor distancia , a la que podrá desplazarse la carga del centro del anillo, puede hallarse basándose en el principio de conservación de la energía
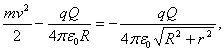
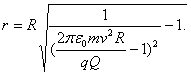
Una esfera metálica de 2m de diámetro se halla en el centro de una gran sala y está cargada con un potencial de 100.000 V. ¿Qué cantidad de calor se desprenderá, si unimos la esfera con la tierra por medio de un conductor?
Solución:
La energía de la esfera cargada es ![]() , donde R es el radio de la esfera y
, donde R es el radio de la esfera y ![]() , su potencial. Durante la descarga esta energía se desprenderá en forma de calor. Calculando, hallamos que
, su potencial. Durante la descarga esta energía se desprenderá en forma de calor. Calculando, hallamos que ![]()
Dos pequeñas esferas son portadoras de cargas diferentes por el valor, pero del mismo signo.Una de las esferas está fija. La segunda esfera, alejándose bajo la acción de las fuerzas electrostáticas de repulsión, puede realizar un trabajo mecánico ![]() . Si antes de iniciarse el movimiento de la segunda esfera, las dos fueron unidas para un cierto tiempo por un conductor, entonces la segunda esfera, alejándose, podrá realizar un trabajo mecánico igual a
. Si antes de iniciarse el movimiento de la segunda esfera, las dos fueron unidas para un cierto tiempo por un conductor, entonces la segunda esfera, alejándose, podrá realizar un trabajo mecánico igual a ![]() . Determinar la cantidad de calor desprendido por el conductor que une las esferas; aclarar a cuenta de qué energía se desprende este calor y varía el trabajo mecánico.
. Determinar la cantidad de calor desprendido por el conductor que une las esferas; aclarar a cuenta de qué energía se desprende este calor y varía el trabajo mecánico.
Solución:
Supongamos que primeramente las cargas de las esferas eran ![]() y
y ![]() . Entonces, el trabajo es
. Entonces, el trabajo es ![]() donde es la distancia entre las esferas. Las cargas de las esferas, después de ser unidas, se hacen iguales a
donde es la distancia entre las esferas. Las cargas de las esferas, después de ser unidas, se hacen iguales a ![]() y el trabajo es
y el trabajo es![]() .No es difícil verificar que
.No es difícil verificar que ![]() .Además, en el conductor que une las cargas, se desprende una cantidad de calor Q. No obstante, la reserva total de energía de las esferas, según el Principio de conservación de la energía, deberá ser igual en ambos casos. Como el trabajo
.Además, en el conductor que une las cargas, se desprende una cantidad de calor Q. No obstante, la reserva total de energía de las esferas, según el Principio de conservación de la energía, deberá ser igual en ambos casos. Como el trabajo ![]() y, respectivamente,
y, respectivamente, ![]() representa la energía potencial de la segunda esfera en el campo de la primera (en el primero y segundo caso), tenemos entonces que
representa la energía potencial de la segunda esfera en el campo de la primera (en el primero y segundo caso), tenemos entonces que
![]()
donde
![]()
Es la energía propia de las esferas hasta el momento de la unión;
![]()
, la energía propia de las esferas después de la redistribución de las cargas (véase el problema 442). La energía que se desprende en forma de calor es
![]()
Una envoltura esférica de radio R está cargada uniformemente con carga Q. Encontrar la fuerza de extensión que actúa sobre la unidad del área de la envoltura.
Solución:
Supongamos que el radio de la envoltura aumente en ![]() , donde
, donde ![]() es un valor infinitamente pequeño. Entonces, la fuerza de extensión realizara un trabajo
es un valor infinitamente pequeño. Entonces, la fuerza de extensión realizara un trabajo ![]() , donde
, donde ![]() es la fuerza que actúa por unidad de área. Este trabajo se realiza gracias a la disminución de la energía electrostática. En el comienzo la energía electrostática es
es la fuerza que actúa por unidad de área. Este trabajo se realiza gracias a la disminución de la energía electrostática. En el comienzo la energía electrostática es ![]() ; después de la extensión ella es:
; después de la extensión ella es: ![]() . La variación de la energía será
. La variación de la energía será
![]()
Y es igual al trabajo A, o sea, ![]() Teniendo en cuenta que el valor
Teniendo en cuenta que el valor ![]() es infinitamente pequeño,
es infinitamente pequeño,
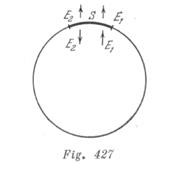
Obtenemos para la fuerza la expresión siguiente: ![]() , donde
, donde ![]() designa la densidad de electricidad, es decir, la carga existente en unidad de área.
designa la densidad de electricidad, es decir, la carga existente en unidad de área.
Podemos también hallar directamente la fuerza incógnita. Examinemos en la esfera una pequeña área S (figura 427). Determinemos la intensidad ![]() del campo eléctrico en el área que estamos analizando, creada por todas las cargas salvo las cargas que se encuentran en la propia área. Para determinarla, analicemos el caso cuando la esfera tiene carga positiva. Designemos por
del campo eléctrico en el área que estamos analizando, creada por todas las cargas salvo las cargas que se encuentran en la propia área. Para determinarla, analicemos el caso cuando la esfera tiene carga positiva. Designemos por ![]() la intensidad del campo eléctrico creado por las cargas que se encuentran en el área examinada. Como dentro de la esfera la intensidad resultante es nula, entonces
la intensidad del campo eléctrico creado por las cargas que se encuentran en el área examinada. Como dentro de la esfera la intensidad resultante es nula, entonces ![]() . La intensidad resultante en la esfera es
. La intensidad resultante en la esfera es ![]() . Por lo tanto,
. Por lo tanto,![]() , de donde
, de donde ![]() . Para hallar la fuerza con que todas las cargas que se encuentran fuera de los limites del área, actúan sobre las cargas que se encuentran en el área, en necesario multiplicar la intensidad
. Para hallar la fuerza con que todas las cargas que se encuentran fuera de los limites del área, actúan sobre las cargas que se encuentran en el área, en necesario multiplicar la intensidad ![]() por el valor de la carga eléctrica del área
por el valor de la carga eléctrica del área ![]()
![]() . La fuerza que actúa sobre la unidad de área será igual a
. La fuerza que actúa sobre la unidad de área será igual a ![]() .
.
¿Qué carga ![]() puede comunicarse a una gota de radio
puede comunicarse a una gota de radio ![]() , si el coeficiente de tensión superficial es igual a
, si el coeficiente de tensión superficial es igual a![]() ?
?
Solución:
![]()
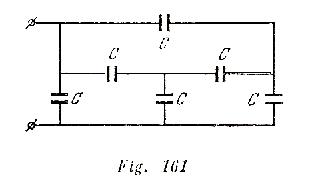
Hallar la capacidad C![]() de una batería de condensadores iguales (fig. 161):
de una batería de condensadores iguales (fig. 161):
Solución:
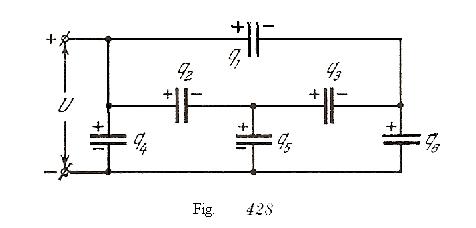
Supongamos que la diferencia de potencial en los terminales de la batería sea ![]() y la carga de la batería sea
y la carga de la batería sea ![]() .Determinar la capacidad de la batería significa determinar la capacidad de un condensador que tenga una tensión
.Determinar la capacidad de la batería significa determinar la capacidad de un condensador que tenga una tensión ![]() para la misma carga
para la misma carga ![]() en las placas como tiene lugar en la batería. Por consiguiente,
en las placas como tiene lugar en la batería. Por consiguiente, ![]() , siendo
, siendo ![]() (fig. 428), y
(fig. 428), y ![]() .El trabajo de las fuerzas del campo electrostático en el paso por el circuito cerrado es nulo; de ahí recibimos que
.El trabajo de las fuerzas del campo electrostático en el paso por el circuito cerrado es nulo; de ahí recibimos que
![]() ,
,
![]()
![]()
Ademas , el conductor que une el segundo, tercero y quinto condensador es eléctricamente neutro. Por lo tanto, ![]() . Resolviendo estas ecuaciones, obtenemos que,
. Resolviendo estas ecuaciones, obtenemos que, ![]() ,
, ![]() y finalmente
y finalmente ![]() .
.
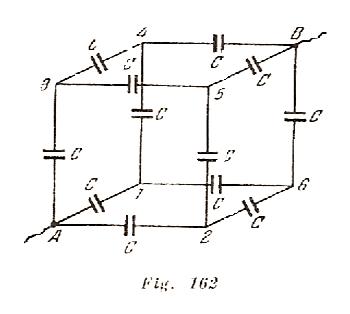
Se hace un cubo de alambre y en cada arista de éste se conecta un condensador de capacidad C(fig. 462).
Encontrar la capacidad de la batería de condensadores, si la batería se asocia al circuito mediante los conductores que unen los vértices opuestos A y B del cubo.
Solución:
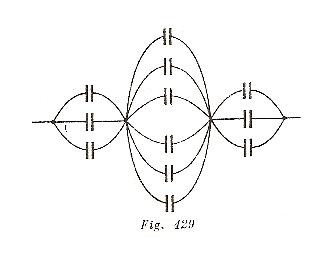
Supongamos que la batería de los condensadores esté cargada .Entonces, los puntos 1,2 y 3 tendrán el mismo potencial y podemos unirlos entre si .Del mismo modo, podemos unir los puntos 4,5 y 6 (fig.162). Como resultado, recibimos un circuito equivalente al que se muestra en la (fig. 429) .La capacidad de los sectores del circuito es 3C, 6C, 3C.La capacidad total se halla de la formula:
![]() =2/3C +1/6C, de donde
=2/3C +1/6C, de donde ![]() =1.2C.
=1.2C.
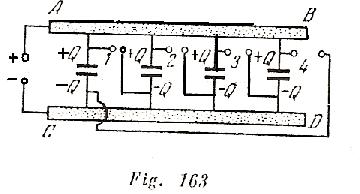
Para obtener altas tensiones de corta duración puede utilizarse el transformador –condensador de chispas de Arkádiev .El circuito de este aparato esta representado el la (fig.163).
Un grupo de condensadores unidos paralelamente por los condensadores AB y CD de una resistencia muy grande, se conecta a la fuente de alta tensión. La placa superior de cada condensador se une, a través de un espacio de chispa, con la placa inferior del condensador siguiente (espacio 1, 2, 3, 4). Cada espacio siguiente es mayor que el anterior. En el momento, cuando la diferencia de potencial entre las armaduras alcance el valor de la tensión disruptiva del primer espacio, tendrá lugar la descarga. En seguida, serán perforados el segundo, el tercero y el cuarto espacio ¿Qué valor alcanzara la diferencia de potencial al perforar el ultimo espacio si hay n condensadores y la tensión aplicada es igual a ![]() ?
?
Solución:
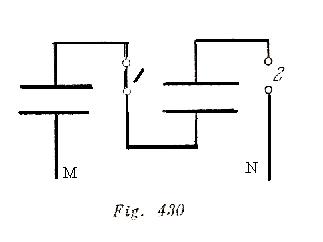
Cuando tiene lugar la descarga en los espacios disruptivos, surge automáticamente la conexión en serie de los condensadores que estaban unidos en paralelo. Entonces la tensión entre las armaduras correspondientes de los condensadores aumenta, puesto que la capacidad del sistema disminuye. En efecto, debido a la gran resistencia de los conductores AB y CD, puede prescindirse de las corrientes que pasan por estos durante la descarga y analizarlas como aisladores a través de los cuales los condensadores no se descargan.
El circuito equivalente, después de la descarga del primer espacio disruptivo, se presenta en la fig. 430. Gracias a la descarga del primer espacio, la diferencia de potencial en el segundo será igual a la suma de las tensiones en el primero y segundo condensadores, es decir, se duplicará. Como consecuencia de esto, comienza la descarga del segundo espacio. En el momento de descarga del enésimo espacio, la tensión en este tendrá un valor ![]() . Las resistencias de los conductores AB y CD deberán ser grandes para que en el momento de la conexión en serie de las placas de los condensadores, durante la descarga de los espacios, los condensadores no se descargan a través de estos conductores.
. Las resistencias de los conductores AB y CD deberán ser grandes para que en el momento de la conexión en serie de las placas de los condensadores, durante la descarga de los espacios, los condensadores no se descargan a través de estos conductores.
Las placas de un condensador plano cargando son puestas a tierra por turno. ¿Se descargará el condensador en este caso?.
Solución:
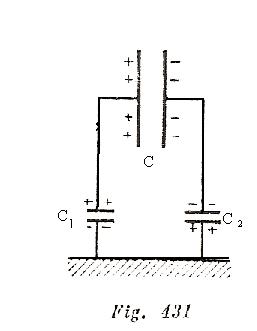
Sí, se descargará. Cada una de las placas posee una determinada capacidad, por lo general no muy grande, respecto a la tierra (en las cercanías de los bordes de las placas, las líneas de fuerza cambian la dirección y alcanzan la tierra). El circuito equivalente se da en la fig. 431. la capacidad de las placas del condensador respecto a la tierra, se representa en forma de las pequeñas capacidades ![]() . Al cerrar la placa izquierda se neutraliza la parte de la carga que se encuentra en ésta. Lo mismo sucede al cerrar la placa derecha. El condensador se descargará tanto mas lento cuanto mayor sea su capacidad en comparación con la capacidad de la placa respecto a la tierra.
. Al cerrar la placa izquierda se neutraliza la parte de la carga que se encuentra en ésta. Lo mismo sucede al cerrar la placa derecha. El condensador se descargará tanto mas lento cuanto mayor sea su capacidad en comparación con la capacidad de la placa respecto a la tierra.
Dos condensadores planos de capacidades ![]() están cargados hasta la diferencia de potencial
están cargados hasta la diferencia de potencial ![]() y
y ![]() , respectivamente (
, respectivamente (![]() ). Demostrar que al conectar estos condensadores en paralelo, la energía electrostática común de los mismos disminuirá. ¿Por qué ocurre esto?
). Demostrar que al conectar estos condensadores en paralelo, la energía electrostática común de los mismos disminuirá. ¿Por qué ocurre esto?
Solución:
La energía total de dos condensadores hasta el momento de unión es
![]()
Después de la unión es
![]()
Se ve fácilmente que ![]() . La diferencia de energías es
. La diferencia de energías es
![]()
Si ![]()
y si ![]()
y ![]() La energía electrostática disminuyó debido a que, durante la conexión de estos condensadores mediante los conductores, las cargas pasaban de un condensador al otro. En los conductores que unen los condensadores se desprendió el calor. La cantidad de calor desprendido no depende de la resistencia de los hilos de conexión. Siendo pequeña la resistencia de los hilos, en ellos pasan grandes corrientes e inversamente.
La energía electrostática disminuyó debido a que, durante la conexión de estos condensadores mediante los conductores, las cargas pasaban de un condensador al otro. En los conductores que unen los condensadores se desprendió el calor. La cantidad de calor desprendido no depende de la resistencia de los hilos de conexión. Siendo pequeña la resistencia de los hilos, en ellos pasan grandes corrientes e inversamente.
Se sabe que los pedazos alargados de un dieléctrico se sitúan a lo largo de las líneas de fuerza de un campo eléctrico. Entre tanto, las moléculas aislados de un dieléctrico no polar, aparentemente deberían extenderse a lo largo del campo y no girar. En un dieléctrico, constituido de moléculas dipolares, el número medio de moléculas que giran, al conectar el campo en el sentido horario, es igual al de moléculas que giran en sentido antihorario. ¿Por qué razón todo el pedazo de dieléctrico girará?
Solución:
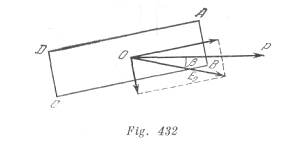
Analicemos para mayor simplicidad un dieléctrico en forma de paralelepípedo homogéneo fuertemente estirado (fig. 432). Descomponemos el campo ![]() donde encuentra el dieléctrico, en componentes dirigidas a lo largo de la barra y perpendicularmente a ésta. Estas componentes provocan el surgimiento de cargas unidas en las superficies AB, CD, BC y AD. El campo de estas cargas unidas entre las superficies AD, BC y AB, DC, debilita las componentes del campo
donde encuentra el dieléctrico, en componentes dirigidas a lo largo de la barra y perpendicularmente a ésta. Estas componentes provocan el surgimiento de cargas unidas en las superficies AB, CD, BC y AD. El campo de estas cargas unidas entre las superficies AD, BC y AB, DC, debilita las componentes del campo ![]() dentro del dieléctrico, teniendo en cuenta que la componente perpendicular a la barra se debilita más, porque las cargas unidas en las superficies AD y BC están distribuidas de una cerca de la otra y su campo es semejante al campo homogéneo de un condensador plano, al mismo tiempo que las cargas situadas en las superficies de pequeña área, se encuentran lejos la una de la otra. Por eso, el campo resultante dentro del dieléctrico no tendrá la misma dirección que el campo
dentro del dieléctrico, teniendo en cuenta que la componente perpendicular a la barra se debilita más, porque las cargas unidas en las superficies AD y BC están distribuidas de una cerca de la otra y su campo es semejante al campo homogéneo de un condensador plano, al mismo tiempo que las cargas situadas en las superficies de pequeña área, se encuentran lejos la una de la otra. Por eso, el campo resultante dentro del dieléctrico no tendrá la misma dirección que el campo ![]() . Por consiguiente, los dipolos creados estarán orientados no a lo largo de cierta dirección OP que forma un ángulo β con
. Por consiguiente, los dipolos creados estarán orientados no a lo largo de cierta dirección OP que forma un ángulo β con ![]() . (Esto se refiere tanto a las moléculas comunes como a las bipolares). Lo que se refiere a las propiedades eléctricas, el dieléctrico polarizado puede considerarse como un gran dipolo que forma un ángulo β con el campo
. (Esto se refiere tanto a las moléculas comunes como a las bipolares). Lo que se refiere a las propiedades eléctricas, el dieléctrico polarizado puede considerarse como un gran dipolo que forma un ángulo β con el campo ![]() . En este campo el girará hasta el momento cuando pare a lo largo del campo. El campo de las cargas unidas es una fuerza interior y no puede provocar la rotación del dieléctrico.
. En este campo el girará hasta el momento cuando pare a lo largo del campo. El campo de las cargas unidas es una fuerza interior y no puede provocar la rotación del dieléctrico.
Una esfera eléctrica, de radio R está polarizada homogéneamente, o sea, los momentos eléctricos dipolares de todas las moléculas son iguales y paralelos los unos a los otros. Encontrar la intensidad del campo eléctrico dentro del dieléctrico, si en unidad de volumen hay N moléculas, cuyo momento bipolar es igual a p=ql.
Solución:
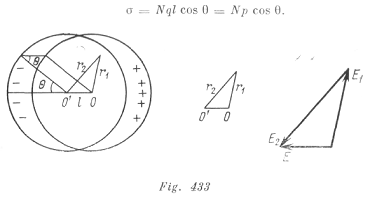
Gracias a la polarización, las cargas se repelerán. Dentro de la esfera con el centro O’ existen cargas negativas y con el centro O, cargas positivas. La densidad cúbica de las cargas es ![]() . La distancia entre los centros O’ y O es l. la intensidad en cualquier punto que se encuentra en la región de superposición entre la dos esferas, puede hallarse a través de una simple construcción geométrica representada en la fig.433. De esta construcción se deduce que la intensidad es
. La distancia entre los centros O’ y O es l. la intensidad en cualquier punto que se encuentra en la región de superposición entre la dos esferas, puede hallarse a través de una simple construcción geométrica representada en la fig.433. De esta construcción se deduce que la intensidad es ![]() . Ella es constante y dirigida en sentido opuesto al vector p. Este campo homogéneo esta, en realidad, creado por las cargas negativas y positivas que se encuentran fuera de la región de superposición. Como
. Ella es constante y dirigida en sentido opuesto al vector p. Este campo homogéneo esta, en realidad, creado por las cargas negativas y positivas que se encuentran fuera de la región de superposición. Como ![]() , entonces podemos considerar que este campo se crea por las cargas superficiales, cuya densidad es.
, entonces podemos considerar que este campo se crea por las cargas superficiales, cuya densidad es.
![]()
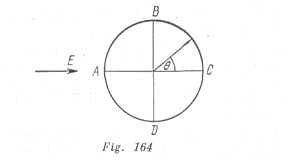
Una esfera dieléctrica se coloca en un campo eléctrico homogéneo, de intensidad igual a E. La constante dieléctrica del material de la esfera es ![]() . Hallar la intensidad del campo dentro de la esfera, así como en los puntos A, B, C y D (fig. 164) que están fuera de la esfera.
. Hallar la intensidad del campo dentro de la esfera, así como en los puntos A, B, C y D (fig. 164) que están fuera de la esfera.
Solución:
No es difícil verificar que el dialéctico estará polarizado de modo homogéneo y que el momento bipolar p de cualquier molécula estará dirigido a lo largo del campo exterior. El campo resultante dentro del dieléctrico tiene una intensidad ![]() . Como
. Como ![]() , donde
, donde ![]() es el coeficiente de polarización de la molécula, entonces
es el coeficiente de polarización de la molécula, entonces ![]() , si consideramos
, si consideramos ![]() , recibimos finalmente para E’ una expresión de la forma siguiente:
, recibimos finalmente para E’ una expresión de la forma siguiente:
![]()
El campo fuera de la esfera, creado por el dieléctrico polarizado, es equivalente al campo de dos cargas puntuales (![]() ) y
) y ![]() situadas en los puntos
situadas en los puntos ![]() y O. Como la distancia
y O. Como la distancia ![]() , entonces para el cálculo de la intensidad resultante en los puntos A, B, C, y D, puede utilizarse la respuesta del problema 420.
, entonces para el cálculo de la intensidad resultante en los puntos A, B, C, y D, puede utilizarse la respuesta del problema 420.
![]()
![]()
Hallar la ley de distribución de la carga superficial en una esfera, sabiendo que dentro de esta última dicha carga crea un campo homogéneo de intensidad E.
Solución:
La densidad superficial de cargas cambia en la esfera según la ley ![]() , donde
, donde ![]() es el ángulo, entre el radio vector y el vector (-E).
es el ángulo, entre el radio vector y el vector (-E).
Una esfera metálica de radio R que tiene carga +Q, fue colocada en un campo eléctrico homogéneo de intensidad E. Encontrar la dependencia de la densidad
superficial de carga en función del ángulo q, así como la intensidad del campo eléctrico en los puntos A, B, C y D (fig. 164), que están fuera de la esfera.
Solución:
![]()
![]()
![]()
![]()
Un cilindro infinito, de material con constante dieléctrica ![]() , está polarizado homogéneamente en dirección perpendicular a su eje. El radio del cilindro es igual a R. El momento dipolar de la molécula es p. El número de moléculas por unidad de volumen es igual a N. Encontrar la intensidad del campo eléctrico dentro del cilindro.
, está polarizado homogéneamente en dirección perpendicular a su eje. El radio del cilindro es igual a R. El momento dipolar de la molécula es p. El número de moléculas por unidad de volumen es igual a N. Encontrar la intensidad del campo eléctrico dentro del cilindro.
Solución:
![]()
Un cilindro infinito de radio R hecho de material con constante dieléctrica ![]() , se mete en un campo eléctrico homogéneo, cuya intensidad E está dirigida perpendicularmente al eje del cilindro. Determinar la intensidad del campo dentro del cilindro, así como en los puntos A, B, C y D fuera del cilindro (fig. 164).
, se mete en un campo eléctrico homogéneo, cuya intensidad E está dirigida perpendicularmente al eje del cilindro. Determinar la intensidad del campo dentro del cilindro, así como en los puntos A, B, C y D fuera del cilindro (fig. 164).
Solución:
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Un cilindro metálico cargado de radio R fue situado en un campo eléctrico homogéneo, cuya intensidad E está dirigida perpendicularmente al eje del cilindro. La carga que cae en unidad de longitud del cilindro es igual a ![]() . Hallar la dependencia de la densidad de la carga en función del ángulo
. Hallar la dependencia de la densidad de la carga en función del ángulo ![]() , así como la intensidad del campo eléctrico en los puntos A, B, C y D (fig. 164) que están fuera del cilindro.
, así como la intensidad del campo eléctrico en los puntos A, B, C y D (fig. 164) que están fuera del cilindro.
Solución:
![]()
![]()
![]()
Una esfera cargada uniformemente con carga q fue instalada en un dieléctrico isotrópico, ilimitado y homogéneo, con constante dieléctrica ![]() . Determinar la carga de polarización en el límite del dieléctrico y la esfera.
. Determinar la carga de polarización en el límite del dieléctrico y la esfera.
Solución:
El campo dieléctrico se crea mediante la carga q y la carga de polarización q’. La intensidad del campo en cualquier punto A que se encuentra fuera de la esfera a una distancia r de su centro, es
![]()
La intensidad E esta unida a la intensidad del campo creado en el vacío por la carga q mediante la relación:
![]()
Por lo tanto,
![]()
De donde resulta que
![]()
El espacio entre dos esferas concéntricas de radios iguales a ![]() y
y ![]() está lleno de dieléctrico con constante dieléctrica e. En el centro de las esferas hay una carga puntual
está lleno de dieléctrico con constante dieléctrica e. En el centro de las esferas hay una carga puntual ![]() . Encontrar la intensidad y el potencial en función de la distancia desde el centro de la esfera, así como el valor de las cargas de polarización.
. Encontrar la intensidad y el potencial en función de la distancia desde el centro de la esfera, así como el valor de las cargas de polarización.
Solución:
Designemos por q el valor de las cargas de polarización. Aplicando el principio de superposición, obtenemos, si ![]()
![]()
![]()
Si ![]() , entonces
, entonces
![]()
![]()
De la ecuación (1) deducimos que ![]() . Por consiguiente, en la región
. Por consiguiente, en la región ![]() , tendremos
, tendremos
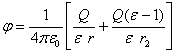
Si ![]() , entonces
, entonces
![]() ,
,
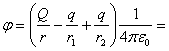
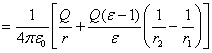
El espacio entre dos esferas metálicas concéntricas finas está lleno de dieléctrico con constante dieléctrica ![]() Los radios de las esferas son iguales a
Los radios de las esferas son iguales a ![]() y
y ![]() . Las cargas de las esferas metálicas, interna y externa, son iguales a
. Las cargas de las esferas metálicas, interna y externa, son iguales a ![]() y
y ![]() , respectivamente. Hallar la diferencia de potencial, la densidad de las cargas de polarización y la capacidad de condensador esférico.
, respectivamente. Hallar la diferencia de potencial, la densidad de las cargas de polarización y la capacidad de condensador esférico.
Solución:
La intensidad del campo en el espacio entre las esferas es
![]()
De donde ![]() = Por consiguiente, la densidad será.
= Por consiguiente, la densidad será.
![]()
No existe campo fuera de la esfera: ![]() E = 0; φ = 0. El potencial φ en la región
E = 0; φ = 0. El potencial φ en la región ![]() es igual a
es igual a
De la última expresión hallamos fácilmente la diferencia de potencial de las esferas:
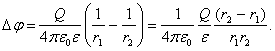
Por consiguiente, la capacidad que es el coeficiente de proporcionalidad entre la carga y la diferencia de potencial de las armaduras del conductor es
![]()
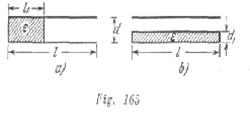
El espacio entre las armaduras de un condensador plano está lleno de dieléctrico con constante dieléctrica ![]() , como muestra la fig. 165. El área de las placas del condensador S. Determinar la capacidad del condensador en ambos casos.
, como muestra la fig. 165. El área de las placas del condensador S. Determinar la capacidad del condensador en ambos casos.
Solución:
a) La capacidad del conductor será igual a la capacidad de los condensadores conectados en paralelo, uno de los cuales está lleno de dieléctrico y el otro no, es decir,
![]() .
.
b) El campo eléctrico entre las armaduras del condensador no cambiará y por lo tanto no cambiará la capacidad si la superficie superior del dieléctrico estará cubierta con una capa infinitamente fina de un conductor. Por eso la capacidad incógnita será igual a la capacidad de dos condensadores conectados en serie:
![]() Donde
Donde ![]() y
y ![]()
Por consiguiente
![]()
Un condensador plano, cuyas placas están cargadas con carga ![]() y
y ![]() fue sumergido hasta la mitad de la altura de las placas en un líquido con constante dieléctrica
fue sumergido hasta la mitad de la altura de las placas en un líquido con constante dieléctrica ![]() . ¿Cuál es la densidad de las cargas de polarización del dieléctrico, si el área de las placas es igual a S?
. ¿Cuál es la densidad de las cargas de polarización del dieléctrico, si el área de las placas es igual a S?
Solución:
La densidad de las cargas de polarización ![]() es
es
![]()
Un dieléctrico consta de moléculas cada una de las cuales puede ser representada en forma de dos cargas![]() y
y ![]() , situadas a una distancia
, situadas a una distancia ![]() la una de la otra. En este caso, la distancia
la una de la otra. En este caso, la distancia ![]() depende de la intensidad del campo E que actúa sobre las cargas de la forma siguiente
depende de la intensidad del campo E que actúa sobre las cargas de la forma siguiente ![]() , donde k es un coeficiente constante.
, donde k es un coeficiente constante.
Supongamos que en unidad de volumen del dieléctrico existe n moléculas. Determinar la intensidad del campo E dentro de un condensador lleno de dicho dieléctrico, si, antes de rellenarlo, la intensidad del campo era igual a ![]() . Determinar la constante dieléctrica del dieléctrico.
. Determinar la constante dieléctrica del dieléctrico.
Solución:
Designemos por E la intensidad total del campo que hallamos en el dieléctrico. La distancia ![]() en que se repelen las cargas en cada molécula, se determina de la relación
en que se repelen las cargas en cada molécula, se determina de la relación ![]() por consiguiente,
por consiguiente,
![]()
![]()
La constante eléctrica se halla de la relación ![]() de donde
de donde
![]()
Un condensador está lleno de dieléctrico, cuyas propiedades están descritas en el problema 472. Encontrar la energía acumulada en el dieléctrico como consecuencia de su polarización.
Solución:
Las cargas ![]() y
y ![]() , al alejarse en la molécula a una distancia
, al alejarse en la molécula a una distancia ![]() , realizan un trabajo
, realizan un trabajo ![]() . La energía acumulada en el dieléctrico es
. La energía acumulada en el dieléctrico es ![]() donde
donde ![]() es el número de moléculas en un volumen V del dieléctrico que se encuentra entre las placas del condensador. De este modo, tenemos
es el número de moléculas en un volumen V del dieléctrico que se encuentra entre las placas del condensador. De este modo, tenemos ![]() Como
Como ![]() entonces
entonces ![]() Expresando
Expresando ![]() por
por ![]() , obtenemos para
, obtenemos para ![]() el valor
el valor
![]()
La energía total del condensador es
![]()
La energía total W puede expresarse como la suma de la energía electrostática ![]() y de la energía acumulada en el dieléctrico,
y de la energía acumulada en el dieléctrico, ![]()
Dos placas metálicas están situadas paralelamente y cargadas con cargas iguales a ![]() y
y ![]() , siendo
, siendo ![]() El espacio entre dos placas está lleno de un dieléctrico homogéneo e isotropito con constante dieléctrica
El espacio entre dos placas está lleno de un dieléctrico homogéneo e isotropito con constante dieléctrica ![]() ¿Cuál será la fuerza que actúa por unidad de área sobre la superficie del dieléctrico? El área de cada placa es igual a S.
¿Cuál será la fuerza que actúa por unidad de área sobre la superficie del dieléctrico? El área de cada placa es igual a S.
Solución:
La fuerza que actúa por unidad de área del dieléctrico es:
![]()
Determinar la energía de un condensador plano, cuyo espacio entre las placas esta lleno de un dieléctrico. Son conocidas la carga del condensador y la diferencia de potencial entre sus armaduras.
Solución:
Supongamos, para simplificar, que dos placas metálicas paralelas, portadoras de cargas ![]() y
y ![]() , estén introducidas en un dieléctrico líquido. La intensidad del campo eléctrico entre las placas es
, estén introducidas en un dieléctrico líquido. La intensidad del campo eléctrico entre las placas es ![]() La intensidad del campo creado por cada placa será igual a
La intensidad del campo creado por cada placa será igual a ![]() Determinemos la fuerza con que actúa la primera placa sobre la segunda. Para esto hace falta multiplicar la intensidad del campo creado por la primera placa, por el valor de la carga que se encuentra en la segunda placa. De este modo
Determinemos la fuerza con que actúa la primera placa sobre la segunda. Para esto hace falta multiplicar la intensidad del campo creado por la primera placa, por el valor de la carga que se encuentra en la segunda placa. De este modo![]() ,
,
Supongamos que la primera placa está sujetada y la segunda puede moverse muy lentamente (podemos prescindir de la variación de la energía mecánica del dieléctrico). El trabajo que puede realizarse por el campo eléctrico durante el movimiento de las placas hasta producirse el contacto, es igual al producto de la fuerza F (la fuerza F es constante) por el valor del desplazamiento d, o sea,![]() Este trabajo se realiza debido a la disminución de la energía eléctrica del condensador. De esta manera la energía electrostática será
Este trabajo se realiza debido a la disminución de la energía eléctrica del condensador. De esta manera la energía electrostática será
![]() ó
ó ![]()
donde U es la diferencia de potencial. La fórmula recibida es válida para cualquier dieléctrico.
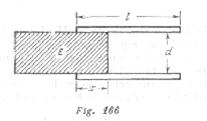
Dos laminas rectangulares de longitud l y área S están situadas paralelamente la una a la a otra a una distancia d. Las láminas tienen una diferencia de potencial igual a U. En el espacio entre las láminas se introduce un dieléctrico con constante dieléctrica ![]() . El grosor del dieléctrico es d, su anchura es igual a la anchura de las placas y su longitud es mayor que l (fig. 166).
. El grosor del dieléctrico es d, su anchura es igual a la anchura de las placas y su longitud es mayor que l (fig. 166).
Encontrar la dependencia de la fuerza, que actúa sobre el dieléctrico por parte del campo en función de la distancia ![]() .
.
Solución:
La energía del condensador en el caso cuando el dieléctrico se desplaza a una distancia ![]() dentro del condensador será
dentro del condensador será
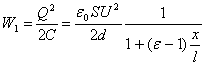
Puesto que ![]() y
y ![]() (véase el problema 470). Si
(véase el problema 470). Si ![]() aumenta en
aumenta en ![]() , entonces la energía disminuirá y será igual a
, entonces la energía disminuirá y será igual a
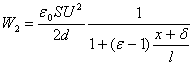
La diferencia de energías
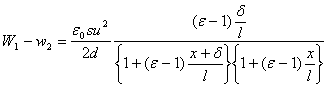
Será igual al trabajo de la fuerza incógnita F en el trayecto. En este trayecto el valor de la fuerza variará, pero, si tomamos ![]() suficientemente pequeño, entonces podemos escribir que
suficientemente pequeño, entonces podemos escribir que
![]()
de donde deducimos que
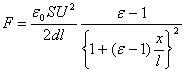
si prescindimos de ![]() en el denominador. Es conveniente recordar que si para calcular la energía nosotros consideramos que el campo dentro del condensador es homogéneo y prescindimos de los efectos de los extremos para la explicación física de la fuerza que actúa sobre el dieléctrico, es preciso tener en cuenta obligatoriamente la heterogeneidad del campo en los extremos.
en el denominador. Es conveniente recordar que si para calcular la energía nosotros consideramos que el campo dentro del condensador es homogéneo y prescindimos de los efectos de los extremos para la explicación física de la fuerza que actúa sobre el dieléctrico, es preciso tener en cuenta obligatoriamente la heterogeneidad del campo en los extremos.
Resolver el problema 476 en el caso, en que la diferencia de potencial entre las placas se mantiene constante e igual a U.
Solución:
La energía del condensador en el caso cuando el dieléctrico se hundió a una distancia x dentro del condensador, será
![]()
Si x aumenta en ![]() , la energía del condensador aumenta en
, la energía del condensador aumenta en
![]()
La carga en las armaduras del condensador durante el movimiento del dieléctrico a una distancia ![]() , aumenta en
, aumenta en
![]()
El trabajo realizado por la batería durante el movimiento de esta cantidad de electricidad será igual a
![]()
Una parte de este trabajo se utiliza para aumentar la energía electrostática del condensador y otra parte, para el movimiento del dieléctrico hacia dentro. Designemos por F, como en el problema anterior, la fuerza con que el dieléctrico se desplaza hacia el interior del condensador. Basándose en el principio de conservación de la energía, podemos escribir que ![]() es decir,
es decir,
![]()
De donde
![]()
Como vemos en este caso la fuerza es constante y no depende de x.
Sobre la superficie de un líquido, puesto en un gran recipiente, se encuentran las placas verticales del condensador que rozan la superficie del líquido. El área de cada placa del condensador es igual a S, la distancia entre las placas, d y la altura de las mimas es l. El condensador se conecta a una batería con f.e.m. igual a U. La densidad del líquido es p y su constante dieléctrica es . Hallar la altura máxima, a la cual se eleva el líquido en el proceso de oscilación, así como la altura del nivel del líquido establecido.
Solución:

El líquido entre las armaduras del condensador (fig. 434) sube bajo la acción de la fuerza
![]()
Cuando el líquido alcanza la altura máxima H, su energía cinética será nula, y la energía potencial aumentara en un valor FH. De la relación
![]()
Determinamos H:
![]()
En esta posición la fuerza de gravedad es mayor que la fuerza F y, como consecuencia de esto, el líquido comenzara a descender.
Para la altura de la columna del líquido igual a
![]()
la energía cinética es máxima y la fuerza F es igual a la fuerza de gravedad. El líquido entre las placas del condensador continúa descendiendo y alcanza el nivel del líquido en el recipiente. El nivel del líquido en el recipiente, debido a sus grandes dimensiones, prácticamente no cambia. De este modo, la altura de la columna cambia periódicamente entre los límites desde O hasta H.
Como consecuencia de fricción, la amplitud de las oscilaciones del líquido disminuirá y el nivel de la columna finalmente se establece a una altura
![]()
Midiendo la altura de elevación h, podemos hallar la constante dieléctrica del líquido e.
En el fondo de un recipiente se encuentra una lámina metálica fina, cuya área S es mucho menor que la del fondo del recipiente. En el recipiente se vierte un líquido con constante dieléctrica ![]() . La profundidad del líquido es mucho menor que las dimensiones lineales de la lámina. ¿Que pasara con el liquido, si cargamos la lamina con una carga igual a + Q?
. La profundidad del líquido es mucho menor que las dimensiones lineales de la lámina. ¿Que pasara con el liquido, si cargamos la lamina con una carga igual a + Q?
Solución:
Una carga libre +Q crea en el dieléctrico un campo eléctrico homogéneo, cuya intensidad es ![]() . Como consecuencia de esto, la capa del dieléctrico de grosor d se polariza. En dos planos que limitan esta capa desde arriba y desde abajo surgen cargas de dolarización. La densidad de las cargas polarizadas
. Como consecuencia de esto, la capa del dieléctrico de grosor d se polariza. En dos planos que limitan esta capa desde arriba y desde abajo surgen cargas de dolarización. La densidad de las cargas polarizadas ![]() es:
es:
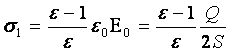
Las cargas Q y la carga negativa ![]() actúan sobre la carga polarizada positiva que se encuentra en la superficie del líquido con una fuerza F dirigida hacia arriba:
actúan sobre la carga polarizada positiva que se encuentra en la superficie del líquido con una fuerza F dirigida hacia arriba:
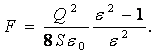
Como consecuencia el nivel del líquido sobre la lámina se eleva a una altura h: