Determinar la velocidad media y la aceleración media de un punto durante 5 y 10 segundos, si su movimiento está dado por el gráfico de velocidad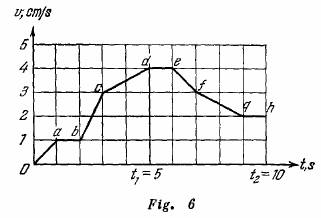
Solución:
Sea S el camino recorrido por el punto en 5 s, numéricamente igual al área encerrada entre la línea quebrada ![]() y el eje de tiempo
y el eje de tiempo ![]() :
: ![]() cm. La velocidad media de movimiento del punto en 5 s es
cm. La velocidad media de movimiento del punto en 5 s es![]() cm/s. La aceleración media del punto en este mismo intervalo de tiempo es
cm/s. La aceleración media del punto en este mismo intervalo de tiempo es ![]()
![]() . El camino recorrido en 10
. El camino recorrido en 10![]() es igual a
es igual a ![]()
![]() . Por consiguiente la velocidad media y la aceleración media son iguales a:
. Por consiguiente la velocidad media y la aceleración media son iguales a: ![]()
![]() y
y ![]()
![]()
Un hombre que se encuentra en la costa abrupta de un lago, tira mediante una cuerda de un bote que está en el agua. La velocidad con que el hombre tira de la cuerda es constante e igual a v. ¿Qué velocidad tendrá el bote en el momento en que el ángulo entre la cuerda y la superficie del agua será igual a ![]() ?
?
Solución:
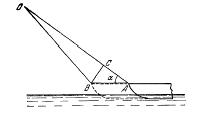
En un pequeño intervalo de tiempo ![]() la proa del bote se desplazara del punto
la proa del bote se desplazara del punto ![]() al punto
al punto ![]() (fig. 281).
(fig. 281). ![]() donde
donde ![]() es la velocidad del bote. En este mismo intervalo de tiempo será recogido un pedazo de la cuerda
es la velocidad del bote. En este mismo intervalo de tiempo será recogido un pedazo de la cuerda ![]() . El
. El ![]() puede considerarse rectangular, ya que
puede considerarse rectangular, ya que ![]() Por consiguiente,
Por consiguiente, ![]()
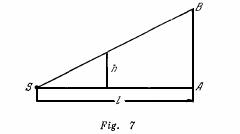
Una fuente de luz puntual ![]()
![]() se encuentre a una distancia de la pantalla vertical
se encuentre a una distancia de la pantalla vertical ![]() . De la fuente a la pantalla por la recta
. De la fuente a la pantalla por la recta ![]() se mueve de modo progresivo, con una velocidad constante
se mueve de modo progresivo, con una velocidad constante![]() , un objeto opaco de altura
, un objeto opaco de altura![]() . Determinar la velocidad instantánea del desplazamiento del extremo superior de la sombra del objeto por la pantalla (fig. 7).
. Determinar la velocidad instantánea del desplazamiento del extremo superior de la sombra del objeto por la pantalla (fig. 7).
Solución
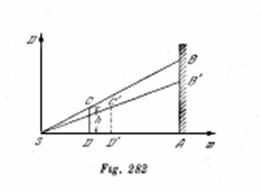
Supongamos que en el momento inicial ![]() el objeto se encontraba en el punto
el objeto se encontraba en el punto ![]() (fig. 282) y en el momento de tiempo igual a
(fig. 282) y en el momento de tiempo igual a ![]() adquirió la posición
adquirió la posición![]() .
.
La semejante de los ![]() nos conduce a la igualdad
nos conduce a la igualdad ![]() ; la velocidad del punto
; la velocidad del punto ![]() , en el momento de tiempo dado, será igual a
, en el momento de tiempo dado, será igual a ![]() , con la condición de que el tiempo
, con la condición de que el tiempo ![]() , durante el cual el extremo de la sombra se desplaza a una distancia igual a
, durante el cual el extremo de la sombra se desplaza a una distancia igual a ![]() tienda a cero. Puesto que:
tienda a cero. Puesto que:
![]()
,
Entonces ![]() , o, considerando que
, o, considerando que ![]() , recibimos:
, recibimos:
![]()
La coordenada de un punto que se mueve por línea recta a lo largo del eje x, varia con el tiempo según la ley ![]() (x es dado en centímetros
(x es dado en centímetros
y t, en segundos). Determinar la velocidad y la aceleración del punto.
Solución:
Para el movimiento uniformemente acelerado tenemos![]() . De esta manera
. De esta manera![]()
![]() ,
, ![]()
![]() y
y ![]()
![]() , donde
, donde ![]() es la coordenada inicial del punto.
es la coordenada inicial del punto.
Un carrito de demostraciones se movía a lo largo de una regla con aceleración constante. En el momento cuando el cronometro indicaba![]() , el carrito se encontraba en el punto
, el carrito se encontraba en el punto ![]() ; en el momento
; en el momento ![]() , en el punto
, en el punto ![]() y en el momento
y en el momento![]() , en el punto
, en el punto ![]() . ¿Qué aceleración tendrá el carrito?
. ¿Qué aceleración tendrá el carrito?
Solución:
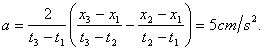
En las figuras 8 y 9 están representados: el grafico de la velocidad de un cuerpo y el grafico de la variación de la coordenada del cuerpo (parábola) en función del tiempo. El comienzo de la lectura del tiempo en ambos gráficos coincide. ¿Serán iguales los movimientos representados en ambos gráficos?
Solución:
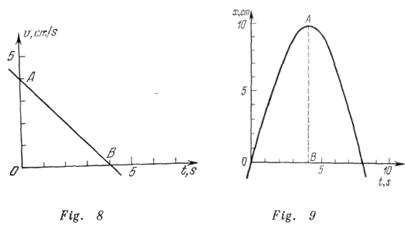
Del grafico de la velocidad (véase la fig. 8) se deduce que la velocidad inicial ![]() (
(![]() ). La aceleración
). La aceleración ![]() Inicialmente la velocidad del cuerpo disminuye. En el momento
Inicialmente la velocidad del cuerpo disminuye. En el momento ![]() la velocidad del cuerpo es igual a cero y después aumenta en magnitud. El segundo grafico (véase la fig. 9) representa también un movimiento uniformemente alterno. Hasta pararse el cuerpo recorre una distancia igual a
la velocidad del cuerpo es igual a cero y después aumenta en magnitud. El segundo grafico (véase la fig. 9) representa también un movimiento uniformemente alterno. Hasta pararse el cuerpo recorre una distancia igual a ![]() Según el grafico anterior el camino recorrido hasta la parada es numéricamente igual al área del
Según el grafico anterior el camino recorrido hasta la parada es numéricamente igual al área del![]() , o sea
, o sea![]() , Por lo tanto, los gráficos representan diferentes movimientos. Al segundo grafico le corresponde otra velocidad inicial:
, Por lo tanto, los gráficos representan diferentes movimientos. Al segundo grafico le corresponde otra velocidad inicial: ![]() y otra aceleración:
y otra aceleración: ![]()

Los puntos A y B se encuentran el uno del otro a una distancia de![]() Del punto A en dirección al punto B salió un automóvil que durante todo el camino se movía uniformemente. Al mismo tiempo del punto B en dirección al punto A salió otro automóvil con velocidad inicial
Del punto A en dirección al punto B salió un automóvil que durante todo el camino se movía uniformemente. Al mismo tiempo del punto B en dirección al punto A salió otro automóvil con velocidad inicial![]() , que tenía una aceleración constante
, que tenía una aceleración constante![]() con la misma dirección que la velocidad del primer automóvil. Es sabido que en el camino los dos automóviles adelantaron el uno al otro dos veces. ¿Dentro de qué límites se encuentra la velocidad del primer automóvil?
con la misma dirección que la velocidad del primer automóvil. Es sabido que en el camino los dos automóviles adelantaron el uno al otro dos veces. ¿Dentro de qué límites se encuentra la velocidad del primer automóvil?
Solución:
El gráfico de movimiento del segundo automóvil tiene la forma de una parábola representada en la (fig. 283) Es evidente que la velocidad del primer automóvil no puede ser excesivamente grande, porque en este caso el adelantamiento ocurre una sola vez (el punto B en la fig. 283, ya que el punto A corresponde al encuentro de los automóviles). La velocidad tampoco puede ser excesivamente pequeña (la recta OC en la fig. 283), puesto que, en el caso contrario, los automóviles jamás pasarán el uno al lado del otro. De tal modo, la ecuación que expresa la igualdad de las coordenadas de los automóviles: ![]() debe tener dos soluciones reales, además, ambas corresponden a momentos ulteriores de tiempo, que el momento de parada (instantánea) del segundo automóvil,
debe tener dos soluciones reales, además, ambas corresponden a momentos ulteriores de tiempo, que el momento de parada (instantánea) del segundo automóvil,
determinada por la igualdad ![]() . De las dos condiciones se deduce que:
. De las dos condiciones se deduce que:
![]() ó
ó ![]()
Una bola cae libremente de una altura H sobre un soporte elástico horizontal. Construir el gráfico de la variación de la coordenada y de la velocidad de la bola en función del tiempo, menospreciando el tiempo del choque. El choque se considera absolutamente elástico.
Solución:
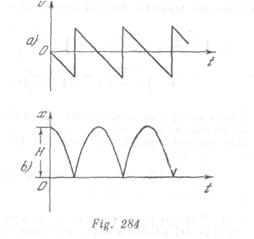
Sobre una placa elástica caen libremente dos bolas de acero. La primera cae desde una altura![]() y la segunda, transcurrido un lapso
y la segunda, transcurrido un lapso ![]() después de la primera, siendo la altura
después de la primera, siendo la altura ![]() . Al pasar cierto tiempo, las velocidades de las bolas coinciden tanto por su valor como por la dirección.
. Al pasar cierto tiempo, las velocidades de las bolas coinciden tanto por su valor como por la dirección.
Determinar el lapso ![]() y el intervalo de tiempo, durante el cual las velocidades de ambas bolas serán iguales. Las bolas no chocan.
y el intervalo de tiempo, durante el cual las velocidades de ambas bolas serán iguales. Las bolas no chocan.
Solución:
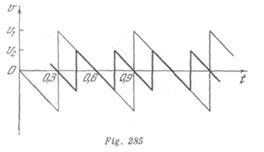
El tiempo de caída de la primera bola es![]() . La relación de las velocidades máximas de las bolas es
. La relación de las velocidades máximas de las bolas es ![]() . Como se deduce del gráfico de velocidades (fig. 285), el tiempo mínimo es
. Como se deduce del gráfico de velocidades (fig. 285), el tiempo mínimo es ![]() s. Además, la segunda bola puede iniciar la caída cada 0,6; 0,9; 1,2 s, etc., después del comienzo de la caída de la primera bola. El tiempo
s. Además, la segunda bola puede iniciar la caída cada 0,6; 0,9; 1,2 s, etc., después del comienzo de la caída de la primera bola. El tiempo ![]() , durante el cual las velocidades de ambas bolas coinciden, es igual a 0,3 s. El proceso se repite periódicamente cada 0,6 s.
, durante el cual las velocidades de ambas bolas coinciden, es igual a 0,3 s. El proceso se repite periódicamente cada 0,6 s.
¿Durante que tiempo un cuerpo que cae libremente sin velocidad inicial, pasa el enésimo centímetro de su trayecto?
Solución:
Las ecuaciones originales son las siguientes:
![]() ,
,
donde es el tiempo de movimiento del cuerpo en el enésimo centímetro del trayecto. De ahí resulta que:
![]() ,
, ![]()
,
![]()
De una torre alta se lanzan dos cuerpos uno tras otro, con velocidades ![]() , de igual valor. El primer cuerpo se lanza verticalmente hacia arriba; pasado cierto tiempo
, de igual valor. El primer cuerpo se lanza verticalmente hacia arriba; pasado cierto tiempo![]()
, se tira el segundo, verticalmente hacia abajo. Determinar la velocidad de los
Cuerpos uno respecto a otro y la distancia entre ellos en el momento ![]()
Solución:
Designando por ![]() y
y ![]() la coordenada y la velocidad del primer cuerpo respecto a la torre y por
la coordenada y la velocidad del primer cuerpo respecto a la torre y por![]() y
y ![]() , la coordenada y la velocidad del segundo, podemos escribir las siguientes ecuaciones:
, la coordenada y la velocidad del segundo, podemos escribir las siguientes ecuaciones:
![]()
![]()
![]()
(Aquí consideramos como positiva la dirección hacia arriba.) La velocidad del primer cuerpo, con relación al segundo, es igual a ![]() y no cambia con el tiempo. La distancia entre los cuerpos es igual a:
y no cambia con el tiempo. La distancia entre los cuerpos es igual a:
![]()
Un cuerpo con relación al otro se mueve uniformemente y por lo tanto la distancia entre ellos cambia linealmente con el tiempo.
Tres puntos ![]() ,
,![]() y
y![]() en el momento inicial están situados en la misma recta horizontal, a distancia igual el uno del otro. El punto
en el momento inicial están situados en la misma recta horizontal, a distancia igual el uno del otro. El punto ![]() comienza a moverse
comienza a moverse
verticalmente hacia arriba con velocidad constante ![]() y el punto C, sin velocidad inicial verticalmente hacia abajo con aceleración constante
y el punto C, sin velocidad inicial verticalmente hacia abajo con aceleración constante ![]() . ¿De qué
. ¿De qué
modo debe moverse el punto ![]() en dirección vertical para que todos los puntos se encuentren todo el tiempo en una recta? Los puntos empiezan a moverse simultáneamente.
en dirección vertical para que todos los puntos se encuentren todo el tiempo en una recta? Los puntos empiezan a moverse simultáneamente.
Solución:
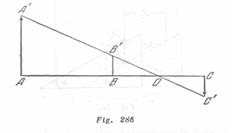
Según las condiciones del problema ![]() (fig.286).De la semejanza de los triángulos
(fig.286).De la semejanza de los triángulos ![]() tenemos:
tenemos:
![]()
Como vernos en la (fig. 286), ![]() Estas relaciones permiten determinar que:
Estas relaciones permiten determinar que:
![]()
De este modo, el punto ![]() se mueve con velocidad inicial
se mueve con velocidad inicial ![]() dirigida hacia arriba y con aceleración constante
dirigida hacia arriba y con aceleración constante![]() , dirigida hacia abajo. Alcanzando una altura igual a
, dirigida hacia abajo. Alcanzando una altura igual a ![]() al punto se moverá hacia abajo.
al punto se moverá hacia abajo.
Un ascensor se mueve con aceleración ![]() . Un pasajero que se encuentra en el ascensor deja caer un libro.
. Un pasajero que se encuentra en el ascensor deja caer un libro.
¿ Cuál será la aceleración del libro con relación al piso del ascensor , si:
1) ¿El ascensor sube?
2) ¿El ascensor baja?
Solución:
El valor de la aceleración del libro respecto al suelo del ascensor no depende de la dirección del movimiento del ascensor (dirección de su velocidad), sino de la dirección de la aceleración del ascensor. Si la aceleración del ascensor está dirigida
hacia arriba, la aceleración del libro será igual ![]() . Si su aceleración está dirigida hacia abajo, la aceleración del libro será igual
. Si su aceleración está dirigida hacia abajo, la aceleración del libro será igual ![]() .
.
Dos automóviles salen de las ciudades ![]() y
y ![]() , el uno al encuentro del otro, con velocidades y aceleraciones
, el uno al encuentro del otro, con velocidades y aceleraciones ![]() de iguales valores. La aceleración del automóvil que salió de la ciudad
de iguales valores. La aceleración del automóvil que salió de la ciudad![]() todo el tiempo tenía dirección hacia
todo el tiempo tenía dirección hacia![]() , y la del automóvil que salió de la ciudad
, y la del automóvil que salió de la ciudad ![]() ,
,
hacia ![]() . ¿Cuánto tiempo más tarde salió uno de estos automóviles si el tercer automóvil que iba todo el tiempo con la velocidad constante
. ¿Cuánto tiempo más tarde salió uno de estos automóviles si el tercer automóvil que iba todo el tiempo con la velocidad constante ![]() . ¿Presenció ambos encuentros de los dos primeros automóviles?
. ¿Presenció ambos encuentros de los dos primeros automóviles?
Solución:
En el momento del encuentro de todos los automóviles, los dos primeros tienen una velocidad única igual a ![]() , con relación al tercero que se mueve uniformemente. En relación a la carretera las velocidades de los automóviles son iguales a
, con relación al tercero que se mueve uniformemente. En relación a la carretera las velocidades de los automóviles son iguales a
![]()
Por eso, la parada (instantánea) de uno de los automóviles tendrá lugar diferentes del primer encuentro, después del intervalo de tiempo igual a ![]() y la segunda, después del intervalo de tiempo igual a
y la segunda, después del intervalo de tiempo igual a![]() , la parada de uno de los automóviles atrasa tanto, cuanto su partida. Por consiguiente, el tiempo de atraso incógnito es:
, la parada de uno de los automóviles atrasa tanto, cuanto su partida. Por consiguiente, el tiempo de atraso incógnito es:
![]()
Un hombre en un ascensor que se mueve con aceleración ![]() , deja caer una bola de una altura
, deja caer una bola de una altura ![]() sobre el piso. Pasado un tiempo
sobre el piso. Pasado un tiempo ![]() del comienzo de la caída de la bola, la aceleración del ascensor cambia su signo y después del lapso
del comienzo de la caída de la bola, la aceleración del ascensor cambia su signo y después del lapso ![]() la aceleración se hace igual a cero. Luego la bola toca el suelo. ¿A qué altura del suelo del ascensor salta la bola después del choque? Considerar el choque absolutamente elástico.
la aceleración se hace igual a cero. Luego la bola toca el suelo. ¿A qué altura del suelo del ascensor salta la bola después del choque? Considerar el choque absolutamente elástico.
Solución:
Si la velocidad del ascensor no cambiase, entonces la bola saltaría a una altura![]() . En el sistema de referencia que tiene una velocidad constante, igual a la velocidad del ascensor, en el momento cuando la bola comienza a caer, el ascensor
. En el sistema de referencia que tiene una velocidad constante, igual a la velocidad del ascensor, en el momento cuando la bola comienza a caer, el ascensor
sube a una altura ![]() en un intervalo de tiempo
en un intervalo de tiempo ![]() y, durante el siguiente intervalo de tiempo igual a
y, durante el siguiente intervalo de tiempo igual a ![]() , sube aún más, a la altura
, sube aún más, a la altura ![]() . La altura total de elevación es
. La altura total de elevación es ![]() La altura incógnita, a la cual saltará la bola sobre el suelo del ascensor, es
La altura incógnita, a la cual saltará la bola sobre el suelo del ascensor, es ![]()
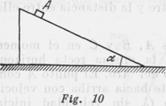
Sobre una cuña, cuyo plano forma un ángulo ![]() con la horizontal, colocaron el cuerpo
con la horizontal, colocaron el cuerpo ![]() (fig. 10). ¿Qué aceleración es necesario transmitir a la cuña en dirección horizontal para que el cuerpo
(fig. 10). ¿Qué aceleración es necesario transmitir a la cuña en dirección horizontal para que el cuerpo ![]() caiga libremente en dirección vertical hacia abajo?
caiga libremente en dirección vertical hacia abajo?
Solución:
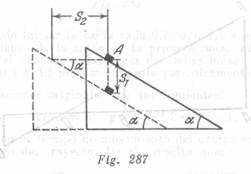
En el intervalo de tiempo t de caída libre el cuerpo ![]() recorrerá por la vertical el trayecto
recorrerá por la vertical el trayecto ![]() .Durante el mismo intervalo de tiempo la cuña deberá desplazarse a una distancia
.Durante el mismo intervalo de tiempo la cuña deberá desplazarse a una distancia ![]() . Si el cuerpo todo el tiempo toca la cuña, es evidente (Se ve en la fig. 287) que
. Si el cuerpo todo el tiempo toca la cuña, es evidente (Se ve en la fig. 287) que ![]() .De esta manera resulta que la aceleración buscada es
.De esta manera resulta que la aceleración buscada es ![]() . Si la aceleración de la cuña en dirección horizontal será mayor que
. Si la aceleración de la cuña en dirección horizontal será mayor que ![]() , entonces el cuerpo se desprende de la cuña.
, entonces el cuerpo se desprende de la cuña.
