Una lancha a motor que va río arriba se encontró con unas balsas que flotaban aguas abajo. Pasada una hora después de este encuentro el motor de la lancha paró. La reparación de éste duró 30 minutos y durante todo ese tiempo la lancha seguía libremente la corriente del río.Arreglado el motor, la lancha comenzó a ir río abajo con la misma velocidad con relación a la corriente del agua y alcanzó las balsas a una distancia de ![]() del punto de su primer encuentro. Determinar la velocidad de la corriente del río, considerándola constante.
del punto de su primer encuentro. Determinar la velocidad de la corriente del río, considerándola constante.
Solución:
En el transcurso de 1 hora, pasada después del encuentro, la lancha se alejaba de las balsas. Durante 30 min., cuando el motor se reparaba, la distancia entre ellas, no aumentaba. La lancha alcanzará las balsas dentro de una hora, ya que la velocidad de la lancha, respecto al agua y por lo tanto a las balsas, permanece constante y es igual a:
![]()
Dos trenes eléctricos salieron de Moscú a Púshkino con un intervalo de ![]() ¿Con qué velocidad iba el tren en dirección a Moscú, si él encontró dos trenes eléctricos, uno después de otro a un intervalo
¿Con qué velocidad iba el tren en dirección a Moscú, si él encontró dos trenes eléctricos, uno después de otro a un intervalo ![]() de minutos?
de minutos?
Solución:
La distancia entre los trenes eléctricos es ![]() por otra parte
por otra parte ![]() De donde
De donde![]()
Un ingeniero trabaja en una fábrica que se encuentra en las cercanías de la ciudad. Cada vez que llega el tren a la estación ferroviaria venía el coche de la fábrica que conducía al ingeniero para el lugar de trabajo. Una vez el ingeniero llegó a la estación una hora antes de lo habitual y sin esperar el coche fue a pie a la fábrica. En el camino encontró el coche y llegó a la fábrica 10 minutos antes de lo corriente. ¿Cuánto tiempo caminó el ingeniero antes de encontrar el coche? (Resolver el problema gráficamente)
Solución:
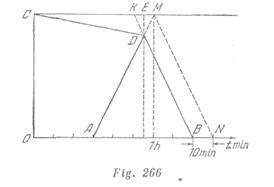
En la fig. 266 ![]() es la representación gráfica del movimiento común del coche.
es la representación gráfica del movimiento común del coche. ![]() Es el gráfico del trayecto del ingeniero hasta encontrar el coche en el punto
Es el gráfico del trayecto del ingeniero hasta encontrar el coche en el punto ![]() .
. ![]() es la representación grafica del movimiento del automóvil después del encuentro con el ingeniero. Según las condiciones del problema
es la representación grafica del movimiento del automóvil después del encuentro con el ingeniero. Según las condiciones del problema ![]() El tiempo del movimiento del ingeniero hasta el encuentro con el coche es igual a:
El tiempo del movimiento del ingeniero hasta el encuentro con el coche es igual a:![]()
Tres turistas que poseen una bicicleta tienen que llegar al centro turístico en el plazo más corto (el tiempo se cuenta por la llegada al centro del último turista). La bicicleta puede llevar sólo a dos personas y por eso el tercer turista tiene que ir a pie. El ciclista lleva al segundo turista hasta un punto determinado del camino, de donde éste continúa andando y el ciclista regresa para coger al tercer turista. Hallar la velocidad media de los turistas, siendo la velocidad del transeúnte ![]() y la del ciclista
y la del ciclista ![]()
Solución:
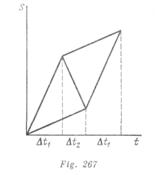
Una vez que el tiempo se calcula con relación al último que llega, éste será el menor posible, cuando todos los tres turistas lleguen al mismo tiempo. EÍ gráfico del movimiento de los turistas está representado en la fig. 267. Del gráfico se deduce que el movimiento a pie del segundo y del tercer turista ocupó un intervalo de tiempo igual a ![]() , donde
, donde ![]() es el tiempo del movimiento de regreso del ciclista. Por lo tanto
es el tiempo del movimiento de regreso del ciclista. Por lo tanto
![]()
![]()
De las ecuaciones resulta que la velocidad media de los turistas es![]()
El correo entre dos atracaderos ![]() y
y ![]() se realiza por medio de los gasolineras. En un tiempo determinado las gasolineras salen de sus atracaderos, se encuentran, se cambian de correspondencias y regresan a sus atracaderos. Si las gasolineras parten de sus atracaderos simultáneamente, la primera que sale del punto
se realiza por medio de los gasolineras. En un tiempo determinado las gasolineras salen de sus atracaderos, se encuentran, se cambian de correspondencias y regresan a sus atracaderos. Si las gasolineras parten de sus atracaderos simultáneamente, la primera que sale del punto ![]() tarda 3 horas en el camino de ida y vuelta y la segunda que sale del punto
tarda 3 horas en el camino de ida y vuelta y la segunda que sale del punto ![]() gasta una hora y media. Las velocidades de ambas gasolineras respecto al agua son iguales. Determinar gráficamente cuánto tiempo más tarde debe salir la gasolinera del punto
gasta una hora y media. Las velocidades de ambas gasolineras respecto al agua son iguales. Determinar gráficamente cuánto tiempo más tarde debe salir la gasolinera del punto ![]() que la gasolinera del punto
que la gasolinera del punto ![]() para que ambas estén en camino el mismo tiempo.
para que ambas estén en camino el mismo tiempo.
Solución:
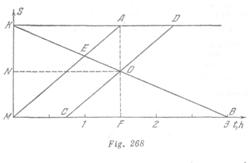
Los gráficos del movimiento de las gasolineras que navegan simultáneamente están representados por las líneas quebradas![]() y
y ![]() , donde
, donde ![]() es el punto de encuentro de las gasolineras (fig. 268). Como la velocidad de las gasolineras respecto al agua, es igual, entonces
es el punto de encuentro de las gasolineras (fig. 268). Como la velocidad de las gasolineras respecto al agua, es igual, entonces ![]() y
y ![]() son líneas rectas. Ambas gasolineras permanecerán en el camino el mismo tiempo, si se encuentran a mitad de la distancia entre los atracaderos.
son líneas rectas. Ambas gasolineras permanecerán en el camino el mismo tiempo, si se encuentran a mitad de la distancia entre los atracaderos.
El punto de encuentro de las gasolineras ![]() está situado en la intersección de la línea
está situado en la intersección de la línea ![]() con la perpendicular trazada del medio del segmento
con la perpendicular trazada del medio del segmento![]() . Los gráficos del movimiento de las gasolineras están representados por las líneas
. Los gráficos del movimiento de las gasolineras están representados por las líneas ![]() y
y ![]() . Como se ve de la figura:
. Como se ve de la figura:![]() y, por consiguiente, el tiempo que queremos encontrar es
y, por consiguiente, el tiempo que queremos encontrar es ![]()
Valiéndose de las condiciones del problema anterior, determinar: la velocidad de la gasolineras con relación al agua, la velocidad de la corriente del río y el lugar de encuentro de las gasolineras en el caso si éstas parten simultáneamente de sus atracaderos. La distancia entre los atracaderos es de ![]() .
.
Solución:
La velocidad de las gasolineras respecto al agua ![]() y la velocidad del río
y la velocidad del río ![]() se determinan de las ecuaciones
se determinan de las ecuaciones![]() donde
donde ![]() y
y ![]() son los tiempos del movimiento de las gasolineras a favor y en contra de la corriente. De acuerdo con las condiciones del problema tenemos
son los tiempos del movimiento de las gasolineras a favor y en contra de la corriente. De acuerdo con las condiciones del problema tenemos ![]() Resolviendo el sistema de ecuaciones, recibimos que:
Resolviendo el sistema de ecuaciones, recibimos que:
El punto de encuentro está situado a una distancia igual a![]() del atracadero
del atracadero ![]()
Del atracadero ![]() al
al ![]() navega un bote de remos; su velocidad respecto al agua es
navega un bote de remos; su velocidad respecto al agua es ![]() Del atracadero
Del atracadero ![]() en dirección al atracadero
en dirección al atracadero ![]() simultáneamente con el bote sale una gasolinera, cuya velocidad
simultáneamente con el bote sale una gasolinera, cuya velocidad ![]() con relación al agua es Durante el movimiento del bote entre los atracaderos la gasolinera cubre cuatro veces esta distancia y llega al atracadero
con relación al agua es Durante el movimiento del bote entre los atracaderos la gasolinera cubre cuatro veces esta distancia y llega al atracadero ![]() al mismo tiempo que el bote. Determinar el sentido de la corriente.
al mismo tiempo que el bote. Determinar el sentido de la corriente.
Solución:
Supongamos que las aguas del río cubren el trayecto de ![]() hasta
hasta ![]() con velocidad
con velocidad ![]() Considerando que el tiempo de movimiento del bote y de la gasolinera es igual, podemos escribir la ecuación
Considerando que el tiempo de movimiento del bote y de la gasolinera es igual, podemos escribir la ecuación
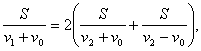
Donde![]() es la distancia entre los atracaderos. De ahí
es la distancia entre los atracaderos. De ahí
![]()
Por lo tanto,
![]()
La solución ![]() debe omitirse, ya que con esta velocidad del río ni el bote ni la gasolinera podrían navegar contra la corriente. Por consiguiente
debe omitirse, ya que con esta velocidad del río ni el bote ni la gasolinera podrían navegar contra la corriente. Por consiguiente ![]() es decir, el río corre del atracadero
es decir, el río corre del atracadero![]() al
al ![]()
Un nombre de altura ![]() pasa cerca de un farol que está suspendido a la altura
pasa cerca de un farol que está suspendido a la altura ![]() sobre la tierra. Encontrar la magnitud y la dirección de la velocidad del movimiento de la sombra proyectada por la cabeza del hombre sobre la tierra, siendo la velocidad del hombre
sobre la tierra. Encontrar la magnitud y la dirección de la velocidad del movimiento de la sombra proyectada por la cabeza del hombre sobre la tierra, siendo la velocidad del hombre ![]()
Solución:

La distancia ![]() del extremo de la sombra partiendo del punto
del extremo de la sombra partiendo del punto ![]() , que se encuentra en la tierra bajo el farol, esta relacionada con la distancia
, que se encuentra en la tierra bajo el farol, esta relacionada con la distancia ![]() del hombre desde el mismo punto mediante la relación
del hombre desde el mismo punto mediante la relación ![]() Por lo tanto, la trayectoria de la sombra es semejante a la del hombre (el centro de similitud se encuentra en el punto
Por lo tanto, la trayectoria de la sombra es semejante a la del hombre (el centro de similitud se encuentra en el punto ![]() ). Por eso el vector de velocidad del extremo de la sombra
). Por eso el vector de velocidad del extremo de la sombra ![]() tiene el mismo sentido que el vector de velocidad
tiene el mismo sentido que el vector de velocidad
Del hombre ![]() y es
y es![]() veces mayor que el hombre (fig. 269).
veces mayor que el hombre (fig. 269).
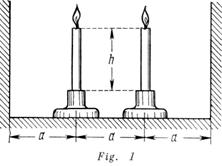
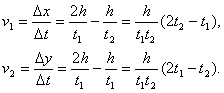
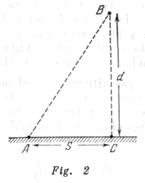
Un hombre se encuentra en la orilla de un lago en el punto ![]() . Le es indispensable en un tiempo sumamente corto llegar al punto
. Le es indispensable en un tiempo sumamente corto llegar al punto ![]() que se encuentra en el lago (fig. 2). La distancia entre el punto
que se encuentra en el lago (fig. 2). La distancia entre el punto ![]() y la orilla es
y la orilla es ![]() y la distancia
y la distancia![]() . La velocidad del movimiento del hombre en el agua es
. La velocidad del movimiento del hombre en el agua es ![]() y por la orilla
y por la orilla ![]()
![]() ¿De qué modo debe ir el hombre: nadar del punto
¿De qué modo debe ir el hombre: nadar del punto ![]() por la recta
por la recta ![]() o primeramente correr por la orilla una cierta distancia y ya después nadar en dirección al punto
o primeramente correr por la orilla una cierta distancia y ya después nadar en dirección al punto ![]() ?
?
Solución:
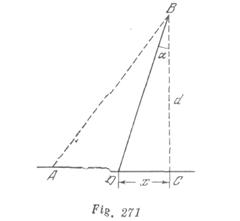
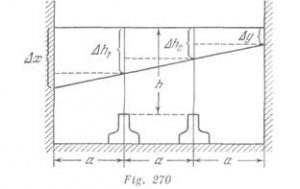
Una vez que la velocidad del movimiento en el agua es menor que la velocidad del movimiento por la orilla, el trayecto ![]() no ocupará obligatoriamente el tiempo mínimo. Supongamos que la trayectoria del movimiento del hombre esté representada por la línea quebrada
no ocupará obligatoriamente el tiempo mínimo. Supongamos que la trayectoria del movimiento del hombre esté representada por la línea quebrada![]() (fig. 271). Es necesario determinar para qué valor de
(fig. 271). Es necesario determinar para qué valor de ![]() el tiempo será el mínimo. El tiempo del movimiento
el tiempo será el mínimo. El tiempo del movimiento ![]() es igual a:
es igual a:
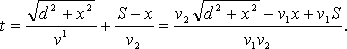
Este tiempo será mínimo si ![]() tiene el valor mínimo. Es evidente que
tiene el valor mínimo. Es evidente que ![]() correspondiente al tiempo mínimo
correspondiente al tiempo mínimo ![]() , no depende de la distancia
, no depende de la distancia ![]() Para determinar
Para determinar ![]() que corresponda al valor mínimo de
que corresponda al valor mínimo de ![]() , expresamos
, expresamos ![]() por
por ![]() y obtenemos una ecuación de segundo grado:
y obtenemos una ecuación de segundo grado:
![]()
La solución de esta ecuación conduce a la siguiente expresión:
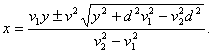
Ya que ![]() no puede ser una magnitud compleja,
no puede ser una magnitud compleja, ![]() El mínimo valor de
El mínimo valor de ![]() será igual a
será igual a ![]() A este valor de
A este valor de ![]() le corresponde el valor de
le corresponde el valor de ![]()
Si ![]() entonces es necesario desde el comienzo nadar por la recta
entonces es necesario desde el comienzo nadar por la recta ![]() en dirección al punto
en dirección al punto ![]() . En caso contrario, es preciso recorrer por la orilla una distancia
. En caso contrario, es preciso recorrer por la orilla una distancia![]() y después nadar en dirección
y después nadar en dirección ![]() a Subrayemos que para el trayecto correspondiente al tiempo mínimo,
a Subrayemos que para el trayecto correspondiente al tiempo mínimo,![]() .
.
Un autobús va por la carretera con velocidad ![]() Un hombre se encuentra a una distancia
Un hombre se encuentra a una distancia ![]() de la carretera y
de la carretera y ![]() del autobús. ¿En qué dirección debe correr el hombre para llegar a un cierto punto de la carretera juntamente
del autobús. ¿En qué dirección debe correr el hombre para llegar a un cierto punto de la carretera juntamente
con el autobús o antes de éste? El hombre puede correr con una velocidad ![]()
Solución:
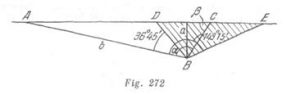
El autobús se encuentra en el punto ![]() y el hombre en el punto
y el hombre en el punto ![]() (fig. 272). El punto
(fig. 272). El punto ![]() es el lugar donde se encuentran los dos,
es el lugar donde se encuentran los dos,![]() es el ángulo entre la dirección hacia el autobús y la que debería recorrer el hombre,
es el ángulo entre la dirección hacia el autobús y la que debería recorrer el hombre,![]() donde
donde ![]() y
y ![]() son los tiempos del movimiento del autobús y el hombre hasta el punto
son los tiempos del movimiento del autobús y el hombre hasta el punto ![]() . Del
. Del ![]() vemos que
vemos que ![]() donde sen
donde sen ![]() Por consiguiente
Por consiguiente![]() Según la condición del problema
Según la condición del problema ![]() por eso
por eso![]() . De donde obtenemos que
. De donde obtenemos que![]()
Las direcciones por las cuales puede correr el hombre, se encuentran dentro de los límites del ángulo ![]() . Corriendo a lo largo de BD ó BE, el hombre alcanzará la autopista simultáneamente con el autobús. Cualquier punto de la autopista que se halle entre los puntos
. Corriendo a lo largo de BD ó BE, el hombre alcanzará la autopista simultáneamente con el autobús. Cualquier punto de la autopista que se halle entre los puntos ![]() y
y ![]() , el hombre alcanzará antes de la llegada del autobús.
, el hombre alcanzará antes de la llegada del autobús.
¿Qué velocidad mínima debe desarrollar el hombre (véase el problema 11) para poder alcanzar el autobús? ¿En qué dirección debe correr el hombre en este caso?
Solución:
La velocidad mínima puede determinarse según las siguientes condiciones:
![]() ,
, ![]() De éstas obtenemos
De éstas obtenemos ![]() siendo
siendo![]() Por lo tanto la dirección en que debe correr el hombre es perpendicular a la del autobús.
Por lo tanto la dirección en que debe correr el hombre es perpendicular a la del autobús.
En un momento dado (véase el problema 11) el autobús se encuentra en el punto![]() y va por la carretera recta
y va por la carretera recta ![]() Hallar el lugar geométrico de los puntos donde el hombre puede encontrarse para alcanzar el autobús?
Hallar el lugar geométrico de los puntos donde el hombre puede encontrarse para alcanzar el autobús?
Solución:
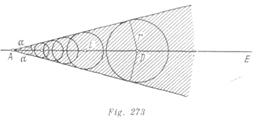
Un punto arbitrario ![]() de la autopista el autobús alcanza en un tiempo
de la autopista el autobús alcanza en un tiempo ![]() donde
donde ![]() es la longitud del trayecto
es la longitud del trayecto![]() de la autopista.
de la autopista. ![]() Este mismo punto en un intervalo de tiempo igual o menor que
Este mismo punto en un intervalo de tiempo igual o menor que ![]() , el hombre podrá llegar, si él se encuentra dentro de los límites del círculo de radio
, el hombre podrá llegar, si él se encuentra dentro de los límites del círculo de radio ![]() y con el centro en el punto
y con el centro en el punto![]() . Dibujando círculos semejantes para otros puntos situados en la autopista, encontramos la región buscada. Los límites de esta región son dos tangentes comunes a los círculos.
. Dibujando círculos semejantes para otros puntos situados en la autopista, encontramos la región buscada. Los límites de esta región son dos tangentes comunes a los círculos.
El ángulo![]() , formado por los límites con la autopista se determina según la igualdad
, formado por los límites con la autopista se determina según la igualdad ![]() (fig273).
(fig273).
Fig. 3
Un hombre debe salir en un bote del punto ![]() al punto
al punto![]() que se encuentra en la orilla opuesta del río (fig. 3). La distancia
que se encuentra en la orilla opuesta del río (fig. 3). La distancia ![]() es igual a
es igual a![]() . La anchura del río
. La anchura del río ![]() ¿Con qué velocidad mínima
¿Con qué velocidad mínima ![]() respecto al agua debe moverse el bote para llegar al punto
respecto al agua debe moverse el bote para llegar al punto ![]() ? La velocidad de la corriente del río es
? La velocidad de la corriente del río es ![]()
Solución:
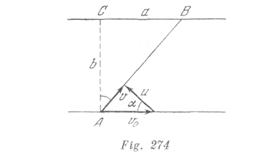
La velocidad del bote ![]() respecto a la orilla, está dirigida hacia
respecto a la orilla, está dirigida hacia ![]() (Fig. 274). Es evidente que
(Fig. 274). Es evidente que ![]() Son conocidas: la dirección del vector
Son conocidas: la dirección del vector![]() , así como el valor y el sentido del vector
, así como el valor y el sentido del vector ![]() El vector
El vector![]() tendrá el valor mínimo, como se ve de la figura cuando
tendrá el valor mínimo, como se ve de la figura cuando ![]() De esta manera
De esta manera
![]()
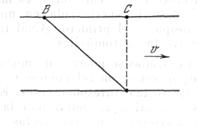
Del punto ![]() situado en la orilla de un río es necesario llegar al punto
situado en la orilla de un río es necesario llegar al punto ![]() , moviéndose siempre por la recta
, moviéndose siempre por la recta ![]() (Fig. 4). La anchura del río
(Fig. 4). La anchura del río ![]() es igual a
es igual a ![]() ; la distancia
; la distancia ![]() , la velocidad máxima del bote con relación al agua es
, la velocidad máxima del bote con relación al agua es ![]() y la velocidad de la corriente es
y la velocidad de la corriente es ![]() ¿Es posible cubrir la distancia en 30 minutos?
¿Es posible cubrir la distancia en 30 minutos?
Solución:
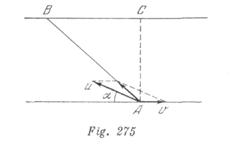
Supongamos que la velocidad ![]() esté dirigida bajo un ángulo
esté dirigida bajo un ángulo ![]() con relación a la orilla (fig. 275). De esta manera resulta que:
con relación a la orilla (fig. 275). De esta manera resulta que:
![]() ,
,![]()
Donde ![]() es el tiempo de movimiento del bote. Excluyendo
es el tiempo de movimiento del bote. Excluyendo ![]()
de estas ecuaciones, obtendremos:
![]()
Resolviendo esta ecuación, recibimos ![]() horas. Por lo tanto, es imposible recorrer la distancia
horas. Por lo tanto, es imposible recorrer la distancia ![]() en 30 minutos.
en 30 minutos.
Por un rió del punto ![]() al punto
al punto ![]() que se encuentra en la orilla opuesta, a lo largo de la recta
que se encuentra en la orilla opuesta, a lo largo de la recta ![]() que forma un ángulo
que forma un ángulo ![]() con la línea de la orilla, navega una gasolinera (fig. 5) el viento sopla con una velocidad
con la línea de la orilla, navega una gasolinera (fig. 5) el viento sopla con una velocidad ![]() en dirección perpendicular a la orilla. La bandera en el mástil de la gasolinera forma un ángulo
en dirección perpendicular a la orilla. La bandera en el mástil de la gasolinera forma un ángulo ![]() con la dirección del movimiento de ésta. Determinar la velocidad de la gasolina respecto a la orilla.
con la dirección del movimiento de ésta. Determinar la velocidad de la gasolina respecto a la orilla.
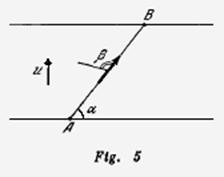
¿Es posible con los datos de este problema determinar la velocidad de la corriente del rió?
Solución:
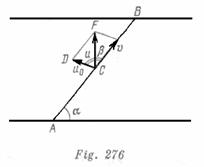
Sea ![]() la velocidad del viento respecto a la gasolinera. Entonces la bandera en la gasolinera estará dirigida a lo largo de
la velocidad del viento respecto a la gasolinera. Entonces la bandera en la gasolinera estará dirigida a lo largo de ![]() . Si v es la velocidad de la gasolinera con relación a la orilla tenemos que
. Si v es la velocidad de la gasolinera con relación a la orilla tenemos que ![]() (fig. 276). En el
(fig. 276). En el ![]() ,
, ![]() y el
y el![]() . Según el teorema de los senos
. Según el teorema de los senos
![]()
De esta igualdad resulta: ![]() . Determinar la velocidad de la corriente del rió por la velocidad conocida de la gasolinera respecto a la orilla, es imposible, ya que desconocemos la dirección de la gasolinera en movimiento respecto al agua.
. Determinar la velocidad de la corriente del rió por la velocidad conocida de la gasolinera respecto a la orilla, es imposible, ya que desconocemos la dirección de la gasolinera en movimiento respecto al agua.
Dos automóviles van con velocidad constante ![]() y
y ![]() por las carreteras que cruzan bajo un ángulo
por las carreteras que cruzan bajo un ángulo ![]() . Determinar el valor y el sentido de la velocidad de un automóvil con relación al otro. ¿Al cabo de que tiempo, después de su encuentro en el cruce, la distancia entre los automóviles será igual a
. Determinar el valor y el sentido de la velocidad de un automóvil con relación al otro. ¿Al cabo de que tiempo, después de su encuentro en el cruce, la distancia entre los automóviles será igual a ![]() ?
?
Solución:
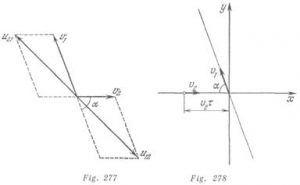
Introduzcamos las siguientes designaciones: ![]() es la velocidad del segundo automóvil respecto al primero,
es la velocidad del segundo automóvil respecto al primero,![]() es la velocidad del primer automóvil respecto al segundo. Es evidente que:
es la velocidad del primer automóvil respecto al segundo. Es evidente que: ![]() y
y ![]() (fig. 277). El tiempo que buscamos es
(fig. 277). El tiempo que buscamos es ![]() .
.
Los automóviles (véase el problema 17) no se encontraron en el cruce de las carreteras; es mas, el segundo automóvil paso la encrucijada en un intervalo de tiempo ![]() después del primero. ¿Cual fue la distancia mínima entre los automóviles?
después del primero. ¿Cual fue la distancia mínima entre los automóviles?
Solución:
Tomemos el momento del paso por el cruce del primer automóvil como origen de la lectura del tiempo. En el sistema de coordenadas representado en la (fig. 278), el movimiento de los automóviles esta expresado por las ecuaciones:
![]() ,
, ![]()
![]() ,
, ![]()
La distancia entre los automóviles en cualquier momento de tiempo es igual a:
![]()
Sustituyendo en esta ecuación los valores de ![]() y
y ![]() , recibimos que:
, recibimos que:
imagen=![]()
Encontrando el mínimo del trinomio cuadrado, obtenemos la distancia mínima que es
![]()
(Véase la resolución del problema 17).
Dos rectas cruzadas se mueven de modo progresivo en direcciones opuestas con velocidades![]() y
y ![]() , perpendiculares a las rectas correspondientes. El ángulo entre las rectas es igual a
, perpendiculares a las rectas correspondientes. El ángulo entre las rectas es igual a ![]() . Determinar la velocidad del punto de intersección de estas rectas.
. Determinar la velocidad del punto de intersección de estas rectas.
Solución
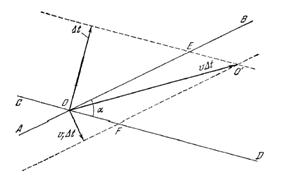
Durante el tiempo ![]() la recta
la recta ![]() se desplazará en una distancia igual a
se desplazará en una distancia igual a ![]()
![]() , la recta
, la recta![]() , en una distancia igual a
, en una distancia igual a ![]()
![]() .
.
Debido a ello, el punto de intersección de las rectas pasará para el punto ![]()
![]() . El desplazamiento
. El desplazamiento ![]() del punto de intersección de las rectas se obtiene del triángulo
del punto de intersección de las rectas se obtiene del triángulo ![]() ó
ó ![]() , donde
, donde
![]()
![]()
De ahí recibimos que:
imagen1![]()
imagen2![]()
imagen3![]()
