Determinar la tensión del cable del péndulo balístico (véase el problema 159), después de ser atravesado por una bala.
Solución:
Valiéndose de la segunda Ley de Newton, podemos escribir ![]() donde
donde ![]() (véase el problema 159), de donde
(véase el problema 159), de donde ![]()
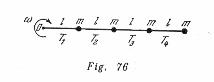
En un hilo elástico no flexible, cuyo peso puede ser despreciad, están sujetos, como se ve en fig. 76, cuatro pesos iguales. Todo el sistema gira con velocidad angular![]() en torno de un eje vertical que pasa a través del punto
en torno de un eje vertical que pasa a través del punto ![]() . Los pesos se mueven por una superficie lisa. Determinar la tensión del cable en diferentes sectores.
. Los pesos se mueven por una superficie lisa. Determinar la tensión del cable en diferentes sectores.
Solución:
![]()
![]()
![]()
![]()
En los extremos de una barra imponderable de longitud![]() están sujetadas en la
están sujetadas en la ![]() y
y ![]() . Las velocidades de las masas
. Las velocidades de las masas ![]() y
y ![]() se encuentran en el mismo plano y son iguales a
se encuentran en el mismo plano y son iguales a ![]() y
y ![]() respectivamente
respectivamente
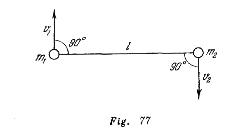
Determinar con qué velocidad se mueve el centro de gravedad del sistema y con qué velocidad angular gira la barra respecto al eje que pasa por el centro de gravedad.
Solución:
Las distancias desde el centro de gravedad hasta los pesos con masas ![]() y
y ![]() son iguales respectivamente a:
son iguales respectivamente a:
![]() .
.
![]() .
.
Designemos por ![]() la velocidad del centro de gravedad, por
la velocidad del centro de gravedad, por ![]() la velocidad angular de rotación. Entonces resulta que
la velocidad angular de rotación. Entonces resulta que![]() y
y ![]() , donde
, donde
![]() ,
,
![]()
En el centro de una plataforma que gira libremente en torno al eje vertical, hay un cañón. El eje de rotación pasa por la culata del mismo. En dirección horizontal, a lo largo del radio de la plataforma fue disparado un tiro. ¿Variará en este caso la velocidad de rotación de la plataforma?
Solución:
La velocidad de rotación disminuirá. La plataforma transmite al proyectil una cantidad de movimiento adicional por la tangente a la trayectoria del extremo del ánima del cañón. Según la tercera ley de Newton, el proyectil expulsado del ánima ejercerá presión sobre la parte interna del ánima dirigida en sentido contrario a la rotación.
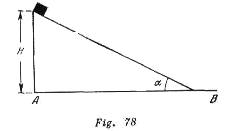
Un pequeño cuerpo comienza a deslizarse sin velocidad inicial por un plano inclinado y altura ![]() (fig. 78). Considerando que no existe fricción y que el choque del cuerpo con el plano horizontal
(fig. 78). Considerando que no existe fricción y que el choque del cuerpo con el plano horizontal ![]() es absolutamente elástico, determinar el carácter del movimiento del cuerpo después de salir del plano inclinado. Responder a la misma pregunta, siendo el choque absolutamente inelástico.
es absolutamente elástico, determinar el carácter del movimiento del cuerpo después de salir del plano inclinado. Responder a la misma pregunta, siendo el choque absolutamente inelástico.
Solución:
En el momento cuando el cuerpo toca el plano horizontal, las componentes horizontal y vertical de la velocidad del cuerpo tendrán valores iguales a ![]() y
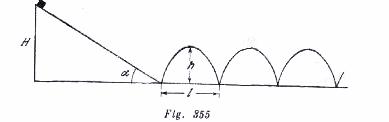
y ![]() . En el caso de un choque absolutamente elástico la componente vertical cambiará el signo y la componente horizontal permanecerá la misma. La trayectoria del cuerpo tendrá la forma de partes de parábolas (fig. 355), siendo
. En el caso de un choque absolutamente elástico la componente vertical cambiará el signo y la componente horizontal permanecerá la misma. La trayectoria del cuerpo tendrá la forma de partes de parábolas (fig. 355), siendo ![]() y
y ![]() . Si el choque es absolutamente inelástico, la componente vertical de la velocidad se hará nula y cuerpo se moverá uniformemente por el plano horizontal con velocidad
. Si el choque es absolutamente inelástico, la componente vertical de la velocidad se hará nula y cuerpo se moverá uniformemente por el plano horizontal con velocidad ![]() .
.
¿Cuál es el radio mínimo del arco que puede describir un motociclista, siendo su velocidad ![]() y el coeficiente de fricción entre los neumáticos y la tierra
y el coeficiente de fricción entre los neumáticos y la tierra![]() ? ¿Bajo que ángulo
? ¿Bajo que ángulo ![]() con la horizontal deberá inclinarse la motocicleta, si consideramos su masa concentrada en el centro?
con la horizontal deberá inclinarse la motocicleta, si consideramos su masa concentrada en el centro?
Solución:
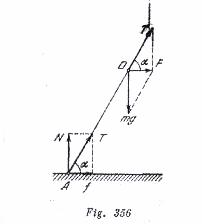
Por parte de la tierra sobre la motocicleta actúan dos fuerzas (fig. 356): ![]() que es la reacción del apoyo y
que es la reacción del apoyo y ![]() que es la fuerza de rozamiento. La suma de estas fuerzas
que es la fuerza de rozamiento. La suma de estas fuerzas ![]() esta dirigida a lo largo de la motocicleta. (en caso contrario respecto al centro de gravedad
esta dirigida a lo largo de la motocicleta. (en caso contrario respecto al centro de gravedad ![]() actuaría el momento de fuerzas que derrumbaría la motocicleta). Sobre el centro de gravedad del cuerpo actúa de este modo la fuerza resultante
actuaría el momento de fuerzas que derrumbaría la motocicleta). Sobre el centro de gravedad del cuerpo actúa de este modo la fuerza resultante ![]() , donde
, donde ![]() es la fuerza de gravedad. Como
es la fuerza de gravedad. Como ![]() , entonces la aceleración centrípeta se transmite a la motocicleta solamente por la fuerza de rozamiento
, entonces la aceleración centrípeta se transmite a la motocicleta solamente por la fuerza de rozamiento![]() . De acuerdo con la segunda ley de Newton tenemos:
. De acuerdo con la segunda ley de Newton tenemos:![]() , siendo
, siendo ![]() . Como se ve en la fig. 356,
. Como se ve en la fig. 356, ![]() ; el valor mínimo de
; el valor mínimo de![]() , obtenido del sistema de ecuaciones dado, es
, obtenido del sistema de ecuaciones dado, es![]() , siendo, en este caso,
, siendo, en este caso,![]() y, por lo tanto,
y, por lo tanto, ![]() .
.
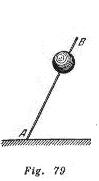
En una barra ligera fue colocada una esfera maciza (fig. 79). ¿En qué caso la barra caerá más rápido: si la colocamos verticalmente en el extremo ![]() o en el extremo
o en el extremo![]() ? El extremo que se encuentra en contacto con el suelo no se desliza.
? El extremo que se encuentra en contacto con el suelo no se desliza.
Solución:
Analicemos una posición intermedia de la barra, cuando ella se inclina con relación a la vertical bajo un ángulo ![]() . Según el principio de conservación de la energía, tenemos
. Según el principio de conservación de la energía, tenemos ![]() , donde
, donde ![]() es la distancia desde el extremo de la barra hasta el centro de gravedad de la esfera. Recibimos, de este modo, que la velocidad angular
es la distancia desde el extremo de la barra hasta el centro de gravedad de la esfera. Recibimos, de este modo, que la velocidad angular![]() se expresa en la siguiente forma:
se expresa en la siguiente forma:
![]() .
.
Para el ángulo dado ![]() ella será tanto menor, cuanto mayor es
ella será tanto menor, cuanto mayor es ![]() . Por consiguiente, la barra caerá mas rápido, si esta colocada en el extremo
. Por consiguiente, la barra caerá mas rápido, si esta colocada en el extremo ![]() .
.
En el extremo de una barra ligera puesta verticalmente en el suelo, fue colocada una esfera maciza. La barra comienza a caer sin velocidad inicial. ¿Para qué ángulo![]() , entre la barra y la vertical, la barra dejará de presionar sobre el suelo? ¿Para qué valor del coeficiente de fricción el extremo de la barra no se deslizará hasta ese momento?
, entre la barra y la vertical, la barra dejará de presionar sobre el suelo? ¿Para qué valor del coeficiente de fricción el extremo de la barra no se deslizará hasta ese momento?
Solución:
De acuerdo con la segunda ley de Newton: ![]() donde
donde ![]() es la fuerza con que la barra deformada actúa sobre la esfera. En el momento cuando cesa la presión de la barra sobre el suelo, su deformación desaparece y
es la fuerza con que la barra deformada actúa sobre la esfera. En el momento cuando cesa la presión de la barra sobre el suelo, su deformación desaparece y![]() . Como fue demostrado en el problema 195,
. Como fue demostrado en el problema 195, ![]() Colocando este valor
Colocando este valor![]() de en la ecuación de movimiento, encontramos el valor de
de en la ecuación de movimiento, encontramos el valor de ![]() de donde
de donde ![]()
A fin de que la barra no deslice, es necesario que sea satisfecha la siguiente condición:![]() Por consiguiente,
Por consiguiente,![]() de donde
de donde ![]()
¿A qué distancia de la base de la barra caerá la esfera (véase el problema 196), si el coeficiente de fricción es ![]()
Solución:
Si ![]() la barra no deslizará hasta el momento cuando
la barra no deslizará hasta el momento cuando![]() no se haga igual a cero, es decir, cuando
no se haga igual a cero, es decir, cuando ![]() Para
Para ![]() de la ecuación
de la ecuación ![]() obtenemos
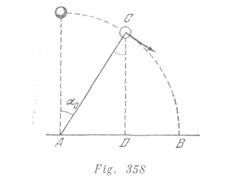
obtenemos ![]() Esto significa que si uno de los extremos estaba fijado en el suelo, la barra fue extendida. Si la barra no está fijada, la esfera comenzará a caer libremente desde el momento cuando el ángulo alcanza el valor igual a
Esto significa que si uno de los extremos estaba fijado en el suelo, la barra fue extendida. Si la barra no está fijada, la esfera comenzará a caer libremente desde el momento cuando el ángulo alcanza el valor igual a ![]() En este momento la velocidad
En este momento la velocidad ![]() forma un ángulo
forma un ángulo ![]() con la horizontal y la altura de la esfera sobre el suelo es
con la horizontal y la altura de la esfera sobre el suelo es ![]() (fig. 358). Aprovechando las leyes de la caída libro, encontraremos la distancia que buscamos:
(fig. 358). Aprovechando las leyes de la caída libro, encontraremos la distancia que buscamos:
![]()
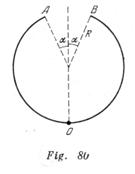
Un alambre está doblado en forma de arco con radio ![]() (fig. 80). En el alambre se asienta una cuenta de vidrio que puede moverse a lo largo del alambre sino inicial la cuenta se encontraba en el punto
(fig. 80). En el alambre se asienta una cuenta de vidrio que puede moverse a lo largo del alambre sino inicial la cuenta se encontraba en el punto ![]() . ¿Qué velocidad horizontal es necesario transmitir a la cuenta a fin de que ésta, recorriendo una parte del trayecto en el aire, caiga nuevamente en el alambre en el punto
. ¿Qué velocidad horizontal es necesario transmitir a la cuenta a fin de que ésta, recorriendo una parte del trayecto en el aire, caiga nuevamente en el alambre en el punto ![]() ?
?
Solución:
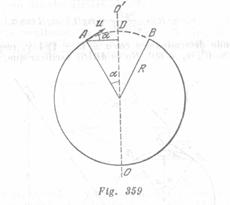
En el segmento ![]() (fig. 359) la cuenta se moverá bajo la acción de fuerza de gravedad. A fin de que ella abandone el alambre en el punto
(fig. 359) la cuenta se moverá bajo la acción de fuerza de gravedad. A fin de que ella abandone el alambre en el punto ![]() y caiga en el punto
y caiga en el punto ![]() , es necesario que el trayecto recorrido horizontalmente por ella sea igual a
, es necesario que el trayecto recorrido horizontalmente por ella sea igual a ![]() Para esto la velocidad de la cuenta en el punto
Para esto la velocidad de la cuenta en el punto ![]() deberá satisfacer la condición:
deberá satisfacer la condición:
![]()
(véase el problema 40). De esta condición obtenemos que ![]()
La cuenta tendrá en el punto ![]() una velocidad
una velocidad ![]() si en el punto
si en el punto ![]() se le transmite una velocidad
se le transmite una velocidad ![]() igual a:
igual a:
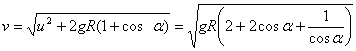
de acuerdo con el principio de conservación de la energía.
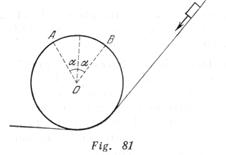
Un cuerpo pequeño se desliza por una superficie inclinada que se transforma en un rizo Nésterov de altura mínima, a fin de que el cuerpo no se desprenda de la superficie del arco (fig. 81). ¿Qué corte simétrico, caracterizado por el ángulo![]() puede ser hecho en el riso para que el cuerpo, recorriendo una parte del camino en el aire, caiga en el punto
puede ser hecho en el riso para que el cuerpo, recorriendo una parte del camino en el aire, caiga en el punto![]() del rizo? ¿Cómo se moverá el cuerpo si el ángulo
del rizo? ¿Cómo se moverá el cuerpo si el ángulo ![]() es mayor o menor que el hallado? La fricción y la resistencia del aire pueden ser despreciadas.
es mayor o menor que el hallado? La fricción y la resistencia del aire pueden ser despreciadas.
Solución:
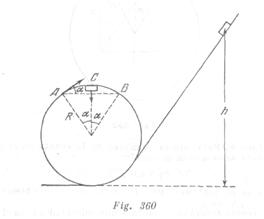
Supongamos que el trayecto no tenga corte. Entonces en el punto ![]() (fig. 360) tenemos
(fig. 360) tenemos
(1)
![]()
Según el principio de conservación de la energía obtenemos:
(2)
![]()
De (1) y (2) recibimos que ![]() La velocidad en el punto
La velocidad en el punto ![]() se determina por el principio de conservación de la energía:
se determina por el principio de conservación de la energía:
(3)
![]()
El cuerpo, cuya dirección de lanzamiento forma un ángulo![]() con la horizontal, volará por la horizontal una distancia igual a:
con la horizontal, volará por la horizontal una distancia igual a:
(4)
![]()
Por otra parte, tenemos
(5)
![]()
De (4) y (5) obtenemos: ![]() Sustituyendo este valor en la ecuación (3), recibimos
Sustituyendo este valor en la ecuación (3), recibimos
![]()
de donde determinamos ![]() y, respectivamente,
y, respectivamente, ![]() No es difícil verificar que, si
No es difícil verificar que, si ![]() el cuerpo caerá dentro del rizo; si
el cuerpo caerá dentro del rizo; si ![]() el cuerpo volará fuera.
el cuerpo volará fuera.
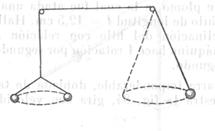
En los extremos de un hilo que pasa a través de dos clavos están sujetos los pesos (fig. 82) que se mueven circularmente. A la izquierda están dos pesos de masa ![]() cada uno, a la derecha, un peso de masa
cada uno, a la derecha, un peso de masa![]() . ¿Estará este sistema en equilibrio?
. ¿Estará este sistema en equilibrio?
Solución:
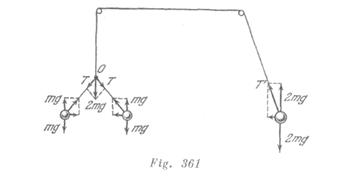
Analicemos las fuerzas que actúan sobre el hilo que se apoya sobre el clavo izquierdo (fig. 361). Las componentes verticales de las fuerzas de tensión ![]() que actúan sobre los cuerpos, son iguales a
que actúan sobre los cuerpos, son iguales a ![]() si el hilo está sujeto al clavo. Sobre el nudo (punto
si el hilo está sujeto al clavo. Sobre el nudo (punto ![]() ), según la tercera ley de Newton, actúan las mismas fuerzas
), según la tercera ley de Newton, actúan las mismas fuerzas ![]() La suma de estas fuerzas está dirigida verticalmente hacía abajo y es igual a
La suma de estas fuerzas está dirigida verticalmente hacía abajo y es igual a ![]() . En el caso de un cuerpo que gira, la componente vertical de la tensión del hilo
. En el caso de un cuerpo que gira, la componente vertical de la tensión del hilo ![]() es
es ![]() (si el cuerpo no desciende). Pero la propia tensión del hilo es
(si el cuerpo no desciende). Pero la propia tensión del hilo es![]() . Por consiguiente este sistema no está en equilibrio. El peso derecho atraerá el hilo a su lado.
. Por consiguiente este sistema no está en equilibrio. El peso derecho atraerá el hilo a su lado.
En un hilo muy fino está colgada una bola. El hilo se pone en posición horizontal y después se suelta. ¿En cuáles puntos de la trayectoria la aceleración de bola estará dirigida verticalmente hacia abajo, en cuáles estará dirigida verticalmente hacia arriba, y en cuáles, horizontalmente? En el momento inicial el hilo no estaba extendido.
Solución:
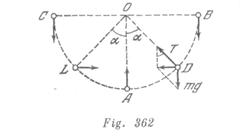
La dirección de la aceleración coincide con la dirección de la fuerza resultante. La aceleración está dirigida verticalmente hacia abajo en las posiciones extremas superiores ![]() y
y ![]() de la bola (fig. 362); verticalmente hacia arriba, en la posición extrema inferior
de la bola (fig. 362); verticalmente hacia arriba, en la posición extrema inferior ![]() y horizontalmente en las posiciones
y horizontalmente en las posiciones ![]() y
y ![]() , determinadas por el ángulo
, determinadas por el ángulo ![]() Encontremos
Encontremos ![]() De acuerdo con la segunda ley de Newton, el producto de la masa por la aceleración centrípeta es igual a la suma de las proyecciones de las fuerzas en dirección del radio de rotación:
De acuerdo con la segunda ley de Newton, el producto de la masa por la aceleración centrípeta es igual a la suma de las proyecciones de las fuerzas en dirección del radio de rotación:
![]()
Por otro lado, como se ve en la fig. 362,![]() . Basándose en el principio de conservación de la energía podemos escribir:
. Basándose en el principio de conservación de la energía podemos escribir:
![]()
De estas ecuaciones hallamos que ![]() y por lo tanto
y por lo tanto ![]()
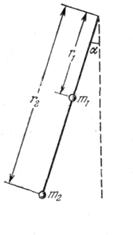
Una barra imponderable puede girar en un plano vertical respecto al punto ![]() En la barra están sujetas dos cargas de masas
En la barra están sujetas dos cargas de masas![]() y
y ![]() a unas distancias
a unas distancias ![]() y
y ![]() del punto
del punto ![]() (fig. 83). La barra fue suelta sin velocidad inicial de una posición que forma un ángulo
(fig. 83). La barra fue suelta sin velocidad inicial de una posición que forma un ángulo ![]() con la vertical. Determinar las velocidades lineales de las cargas de masas
con la vertical. Determinar las velocidades lineales de las cargas de masas ![]() y
y![]() en el momento, cuando la barra está en posición vertical.
en el momento, cuando la barra está en posición vertical.
Solución:
Designemos por ![]() la velocidad angular de la barra en el momento cuando ella pasa por la vertical. Basándose en el principie de conservación de la energía, podemos escribir:
la velocidad angular de la barra en el momento cuando ella pasa por la vertical. Basándose en el principie de conservación de la energía, podemos escribir:
![]()
ó
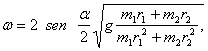
de donde recibimos que
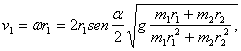
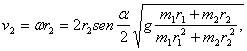
En el eje de una máquina centrífuga fue colocada una pesa de plomo, a la cual fue atada una pequeña bola en un hilo de longitud ![]() Hallar el ángulo
Hallar el ángulo ![]() de inclinación del hilo con relación a la vertical, si la máquina hace 1 rotación por segundo, 2 rotaciones por segundo.
de inclinación del hilo con relación a la vertical, si la máquina hace 1 rotación por segundo, 2 rotaciones por segundo.
Solución:
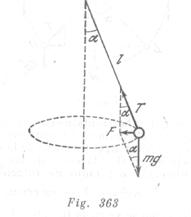
La resultante de las fuerzas aplicadas a la bola,![]() deberá crear una aceleración centrípeta donde
deberá crear una aceleración centrípeta donde ![]() (fig. 363). De ahí resulta que:
(fig. 363). De ahí resulta que: ![]() Esta ecuación tiene dos soluciones:
Esta ecuación tiene dos soluciones:
![]()
![]()
En segundo caso son válidas ambas soluciones: ![]() (en esta condición la bola se encuentra en equilibrio inestable)
(en esta condición la bola se encuentra en equilibrio inestable) ![]() y a = 60°. En primer caso es válida solamente la solución
y a = 60°. En primer caso es válida solamente la solución ![]()
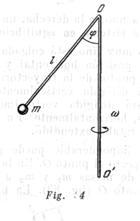
Una barra imponderable, doblada de tal forma como lo muestra la fig. 84, gira con velocidad angular ![]() respecto al eje En el extremo de la barra está sujeto un peso de masa
respecto al eje En el extremo de la barra está sujeto un peso de masa ![]() . Determinar la fuerza con que la barra actúa sobre el peso
. Determinar la fuerza con que la barra actúa sobre el peso ![]() .
.
Solución:
Descomponemos la fuerza ![]() con que la barra actúa sobre el peso
con que la barra actúa sobre el peso ![]() , en las componentes perpendiculares entre sí
, en las componentes perpendiculares entre sí ![]() y
y ![]() (fig. 364). Proyectemos las fuerzas en la vertical y en la horizontal y escribamos las ecuaciones de Newton para estas direcciones:
(fig. 364). Proyectemos las fuerzas en la vertical y en la horizontal y escribamos las ecuaciones de Newton para estas direcciones:
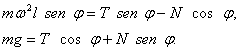
De estas ecuaciones determinaremos ![]() y
y ![]() :
:
Por consiguiente resulta que
![]()
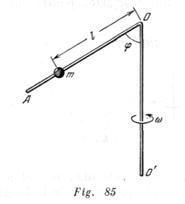
Una barra imponderable ![]() doblada como muestra la fig. 85, gira con velocidad angular
doblada como muestra la fig. 85, gira con velocidad angular ![]() respecto al eje
respecto al eje ![]() En la barra fue asentada una cuenta de vidrio de masa
En la barra fue asentada una cuenta de vidrio de masa ![]() . Determinar a qué distancia
. Determinar a qué distancia ![]() del punto
del punto ![]() la cuenta estará en equilibrio, si el coeficiente de fricción entre la cuenta y la barra es igual a
la cuenta estará en equilibrio, si el coeficiente de fricción entre la cuenta y la barra es igual a ![]()
Solución:
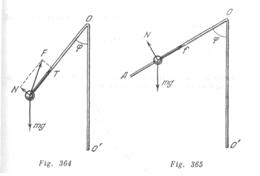
Las fuerzas que actúan sobre la cuenta se ven en la fig. 365:![]() es la fuerza de rozamiento;
es la fuerza de rozamiento;![]() , la fuerza de gravedad;
, la fuerza de gravedad; ![]() , la fuerza normal de la reacción. Las ecuaciones de Newton para las proyecciones de las fuerzas en direcciones horizontal y vertical, tienen la forma
, la fuerza normal de la reacción. Las ecuaciones de Newton para las proyecciones de las fuerzas en direcciones horizontal y vertical, tienen la forma
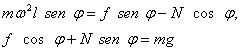
De estas ecuaciones hallamos que
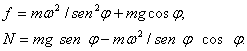
En caso de equilibrio tenemos ![]()
ó ![]() de donde tenemos que
de donde tenemos que ![]() En un caso particular
En un caso particular ![]()
En una barra vertical que gira con velocidad angular ![]() fue atado un hilo de longitud
fue atado un hilo de longitud ![]() , en cuyo extremo se encuentra un peso de masa
, en cuyo extremo se encuentra un peso de masa ![]() . Al peso, a su vez, fue atado otro hilo de la misma longitud que en su extremo tiene un segundo peso de masa
. Al peso, a su vez, fue atado otro hilo de la misma longitud que en su extremo tiene un segundo peso de masa ![]() . Demostrar que el ángulo entre el primer hilo y la vertical será menor que el ángulo entre la vertical y el segundo hilo. El peso del hilo puede ser prescindido.
. Demostrar que el ángulo entre el primer hilo y la vertical será menor que el ángulo entre la vertical y el segundo hilo. El peso del hilo puede ser prescindido.
Solución:

En la fig. 366 se dan las fuerzas que actúan sobre los pesos.![]() y
y ![]() son las tensiones de los hilos. Escribamos las ecuaciones de Newton para las proyecciones en direcciones horizontal y vertical: para el primer peso
son las tensiones de los hilos. Escribamos las ecuaciones de Newton para las proyecciones en direcciones horizontal y vertical: para el primer peso
![]()
para el segundo peso
![]()
Excluyendo ![]() y
y ![]() del sistema de ecuaciones (1) y (2), hallamos las siguientes ecuaciones:
del sistema de ecuaciones (1) y (2), hallamos las siguientes ecuaciones:
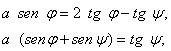
donde ![]() De estas ecuaciones deducimos que
De estas ecuaciones deducimos que ![]() y por consiguiente
y por consiguiente ![]()
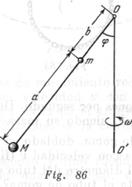
En una barra imponderable están atados dos pesos de masas ![]() y
y ![]() . La barra, mediante una articulación, está unida al eje vertical
. La barra, mediante una articulación, está unida al eje vertical ![]() (fig. 86). El eje
(fig. 86). El eje ![]() ira con velocidad angular
ira con velocidad angular![]() . Determinar el ángulo
. Determinar el ángulo ![]() formado por la barra y la vertical.
formado por la barra y la vertical.
Solución:
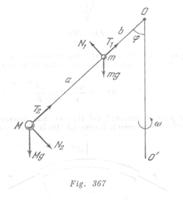
Las fuerzas que actúan sobre los pesos se muestran en la fig. 367. ![]() y
y ![]() son las componentes de las fuerzas, con que la barra actúa sobre los pesos
son las componentes de las fuerzas, con que la barra actúa sobre los pesos ![]() y
y![]() .
. ![]() y
y ![]() están dirigidas en sentidos opuestos, porque la suma de los momentos de las fuerzas que actúan sobre la barra respecto al punto
están dirigidas en sentidos opuestos, porque la suma de los momentos de las fuerzas que actúan sobre la barra respecto al punto ![]() es nula debido a la imponderabilidad de la barra:
es nula debido a la imponderabilidad de la barra: ![]() Las ecuaciones de movimiento de los pesos para las proyecciones en direcciones horizontal y vertical tienen la siguiente forma:
Las ecuaciones de movimiento de los pesos para las proyecciones en direcciones horizontal y vertical tienen la siguiente forma:

Excluyendo del sistema las incógnitas ![]() y
y ![]() encontramos que:
encontramos que:
1)![]()
2) ![]()
La primera solución es valida para cualquier velocidad angular de rotación y la segunda para 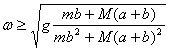 (véase la resolución del problema 203).
(véase la resolución del problema 203).
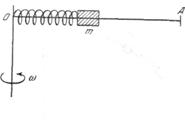
Una barra horizontal recta gira con velocidad angular constante en torno de un eje vertical. Un cuerpo puede deslizarse por la barra sin fricción. Inicialmente el cuerpo se mantiene en posición de equilibrio mediante un muelle (fig. 87). ¿Qué pasará con el cuerpo si le transmitimos una velocidad inicial a lo largo de la barra? Es posible prescindir de la longitud del muelle suelto.
Solución:
En equilibrio tenemos ![]() , donde
, donde ![]() es la distancia del cuerpo hasta el eje. De ahí se ve claramente que para cualquier
es la distancia del cuerpo hasta el eje. De ahí se ve claramente que para cualquier ![]() el muelle transmite al cuerpo la aceleración centrípeta necesaria para la rotación. Por eso después de que el cuerpo ha sido empujado, éste puede moverse con velocidad constante hasta el apoyo
el muelle transmite al cuerpo la aceleración centrípeta necesaria para la rotación. Por eso después de que el cuerpo ha sido empujado, éste puede moverse con velocidad constante hasta el apoyo ![]() o hasta el momento cuando se verifique para el muelle la ley de la proporcionalidad directa entre la fuerza y la deformación.
o hasta el momento cuando se verifique para el muelle la ley de la proporcionalidad directa entre la fuerza y la deformación.
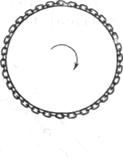
Una cadena metálica de longitud ![]() cuyos extremos están unidos, fue colocada en un disco de madera (fig. 88). El disco gira con una velocidad
cuyos extremos están unidos, fue colocada en un disco de madera (fig. 88). El disco gira con una velocidad ![]() rotaciones por segundo. Determinar la tensión de la cadena
rotaciones por segundo. Determinar la tensión de la cadena ![]() 71, siendo su masa
71, siendo su masa![]()
Solución:
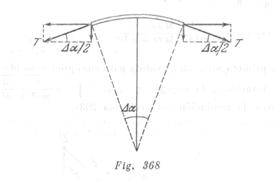
Escribamos la segunda ley de Newton para un pequeño segmento de la cadena de masa![]() mostrado en la fig. 368:
mostrado en la fig. 368:
![]()
Como el ángulo ![]() es pequeño, entonces
es pequeño, entonces ![]() de donde
de donde ![]()
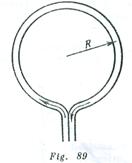
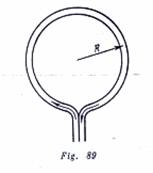
Por un tubo de goma, doblado en forma de un anillo, circula el agua con velocidad ![]() (Fig. 89). El radio del anillo es
(Fig. 89). El radio del anillo es ![]() el diámetro del tubo es
el diámetro del tubo es![]() ¿Con que fuerza se dilata
¿Con que fuerza se dilata
el tubo de goma?
Solución:
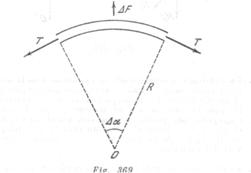
Destaquemos un pequeño segmento del tubo de longitud ![]() (fig. 369). Las paredes extendidas del tubo transmiten al líquido que pasa por este segmento una aceleración
(fig. 369). Las paredes extendidas del tubo transmiten al líquido que pasa por este segmento una aceleración ![]() Por la tercera ley de Newton el líquido actúa sobre este segmento con una fuerza
Por la tercera ley de Newton el líquido actúa sobre este segmento con una fuerza
![]()
donde![]() es la densidad del líquido. Las fuerzas de tensión
es la densidad del líquido. Las fuerzas de tensión ![]() del anillo compensan la fuerza
del anillo compensan la fuerza ![]() De la condición de equilibrio y considerando que
De la condición de equilibrio y considerando que ![]() es pequeño, tenemos:
es pequeño, tenemos:
![]()
Por consiguiente la fuerza que hallamos es ![]()
Una barra homogénea de longitud ![]() y de masa
y de masa ![]() gira con una velocidad angular
gira con una velocidad angular ![]()
en un plano horizontal, en torno al eje que pasa por su extremo. Encontrar la tensión de la barra a distancia ![]() de su eje de rotación.
de su eje de rotación.
Solución:
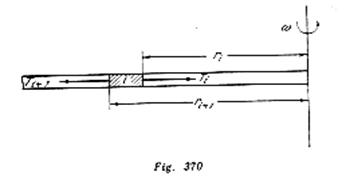
Dividamos la barra en ![]() secciones de igual longitud y analicemos una sección cualquiera con índice
secciones de igual longitud y analicemos una sección cualquiera con índice ![]() (fig. 370). Las aceleraciones de los diferentes puntos de esta sección serán diferentes, ya que las distancias desde los puntos hasta el eje de rotación son diferentes. No obstante si la diferencia
(fig. 370). Las aceleraciones de los diferentes puntos de esta sección serán diferentes, ya que las distancias desde los puntos hasta el eje de rotación son diferentes. No obstante si la diferencia ![]() es pequeña, podemos considerar que la aceleración de la sección
es pequeña, podemos considerar que la aceleración de la sección ![]() es igual a
es igual a ![]() que será tanto más exacta, cuanto menor es la longitud de la sección
que será tanto más exacta, cuanto menor es la longitud de la sección![]() .
.
Sobre la sección ![]() actúa la fuerza elástica
actúa la fuerza elástica ![]() por parte de la sección deformada
por parte de la sección deformada ![]() y la fuerza
y la fuerza ![]() por parte de la sección
por parte de la sección ![]() . Como la masa de la sección
. Como la masa de la sección ![]() es igual a
es igual a ![]() , entonces, basándose en la segunda ley de Newton, podemos escribir:
, entonces, basándose en la segunda ley de Newton, podemos escribir:
![]()
o
![]()
Escribimos las ecuaciones de movimiento para las secciones desde ![]() hasta
hasta ![]() , considerando que
, considerando que ![]() y
y ![]()
![]()
![]()
……………….…………………..
![]()
![]()
En la primera ecuación de este sistema consideramos que la fuerza elástica no actúa sobre el extremo de la barra, o sea,![]() . Sumando las ecuaciones del sistema obtenemos que la tensión que buscamos es
. Sumando las ecuaciones del sistema obtenemos que la tensión que buscamos es ![]() . Cuando más cerca están las secciones de la barra del eje de rotación, tanto mayor será el grado de tensión de estas secciones de la barra.
. Cuando más cerca están las secciones de la barra del eje de rotación, tanto mayor será el grado de tensión de estas secciones de la barra.
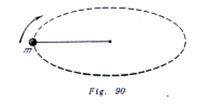
Una bola de masa ![]() , fijada en una barra imponderable, gira con velocidad constante
, fijada en una barra imponderable, gira con velocidad constante![]() en un plano horizontal (fig. 90). La energía cinética de la bola en el sistema de coordenadas inmóvil respecto al eje de rotación es constante e igual a
en un plano horizontal (fig. 90). La energía cinética de la bola en el sistema de coordenadas inmóvil respecto al eje de rotación es constante e igual a ![]() . Con relación al sistema de coordenadas de movimiento rectilíneo en un plano horizontal, con velocidad
. Con relación al sistema de coordenadas de movimiento rectilíneo en un plano horizontal, con velocidad ![]() con relación al eje, la energía cinética varía en el transcurso del tiempo de cero a
con relación al eje, la energía cinética varía en el transcurso del tiempo de cero a ![]() . ¿Cuál es la causa de este cambio de energía?
. ¿Cuál es la causa de este cambio de energía?
Solución:
En un sistema de referencia inmóvil con relación al eje, la fuerza de tensión de la barra no realiza trabajo, ya que ésta todo el tiempo está dirigida perpendicularmente a la velocidad de la bola. En un sistema en movimiento esta fuerza realiza un trabajo diferente de cero y debido a este trabajo cambia la energía cinética de la bola.
Un aro homogéneo y fino rueda por una superficie horizontal con una velocidad constante![]() . ¿Cómo y bajo la acción de qué fuerzas varía la energía total de un pequeño sector
. ¿Cómo y bajo la acción de qué fuerzas varía la energía total de un pequeño sector ![]() que se encuentra en un momento dado en el punto más alto del aro?
que se encuentra en un momento dado en el punto más alto del aro?
Solución:
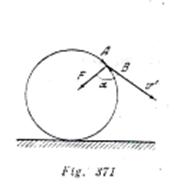
Un sector del aro ![]() de masa
de masa ![]() posee en la posición más alta una energía
posee en la posición más alta una energía ![]() . Las energías cinética y potencial del sector
. Las energías cinética y potencial del sector ![]() comienzan a disminuir durante el movimiento. La pérdida de la energía tiene lugar como consecuencia del trabajo de las fuerzas de deformación elástica del aro, cuya resultante es la fuerza centrípeta siempre dirigida hacia el centro. La velocidad del sector
comienzan a disminuir durante el movimiento. La pérdida de la energía tiene lugar como consecuencia del trabajo de las fuerzas de deformación elástica del aro, cuya resultante es la fuerza centrípeta siempre dirigida hacia el centro. La velocidad del sector ![]() forma un ángulo obtuso con la fuerza
forma un ángulo obtuso con la fuerza ![]() (fig. 371). Por eso el trabajo de la fuerza
(fig. 371). Por eso el trabajo de la fuerza![]() es negativo y, por consiguiente, se disminuye la energía del sector de masa
es negativo y, por consiguiente, se disminuye la energía del sector de masa ![]() . Como el sector
. Como el sector ![]() pasa por la posición extrema inferior, el trabajo de la fuerza
pasa por la posición extrema inferior, el trabajo de la fuerza ![]() , como es fácil ver, se hace positivo y la energía del sector
, como es fácil ver, se hace positivo y la energía del sector ![]() comienza a aumentar.
comienza a aumentar.
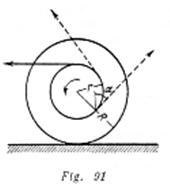
Un hilo está arrollado en una bobina pesada, la cual se encuentra en una superficie horizontal áspera, por donde puede rodar sin deslizamiento. Si se tira del hilo en dirección horizontal hacia la izquierda, la bobina también rodará para la izquierda. Si la dirección del hilo cambia (fig. 91), entonces, para cualquier valor del ángulo ![]() entre la dirección del hilo y la vertical, la bobina rodará hacia la derecha. Determinar este ángulo. ¿Qué ocurrirá con la bobina para el valor del ángulo dado? El radio de la parte externa de la misma es
entre la dirección del hilo y la vertical, la bobina rodará hacia la derecha. Determinar este ángulo. ¿Qué ocurrirá con la bobina para el valor del ángulo dado? El radio de la parte externa de la misma es ![]() , de la interna es
, de la interna es![]() .
.
Solución:
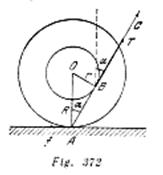
Tracemos del punto ![]() que es «el eje instantáneo de rotación» (véase el problema 57), una tangente a la circunferencia interna de la bobina (fig. 372). Si la dirección del hilo coincide con la dirección de la tangente
que es «el eje instantáneo de rotación» (véase el problema 57), una tangente a la circunferencia interna de la bobina (fig. 372). Si la dirección del hilo coincide con la dirección de la tangente ![]() , el momento de las fuerzas que hacen la bobina con relación al eje instantáneo, será nulo. Por eso la bobina que está en reposo no girará alrededor del eje instantáneo y, por consiguiente, no rodará. El valor del ángulo
, el momento de las fuerzas que hacen la bobina con relación al eje instantáneo, será nulo. Por eso la bobina que está en reposo no girará alrededor del eje instantáneo y, por consiguiente, no rodará. El valor del ángulo ![]() , para que tiene lugar el cambio de la dirección del movimiento de la bobina se determina del triángulo
, para que tiene lugar el cambio de la dirección del movimiento de la bobina se determina del triángulo ![]() :
: ![]() . Si la inclinación del hilo es mayor que
. Si la inclinación del hilo es mayor que ![]() , la bobina rodará hacia la derecha, si es menor, rodará hacia la izquierda con condición de que no haya deslizamiento. Si la tensión del hilo
, la bobina rodará hacia la derecha, si es menor, rodará hacia la izquierda con condición de que no haya deslizamiento. Si la tensión del hilo ![]() satisface la condición
satisface la condición![]() , donde
, donde ![]() es la fuerza de rozamiento, entonces la bobina permanece inmóvil. En caso contrario para el valor de
es la fuerza de rozamiento, entonces la bobina permanece inmóvil. En caso contrario para el valor de ![]() ella comienza a girar en su lugar alrededor del punto
ella comienza a girar en su lugar alrededor del punto ![]() en sentido antihorario.
en sentido antihorario.
Encontrar la energía cinética de un aro de masa ![]() y de radio
y de radio![]() , si el aro se mueve uniformemente con una velocidad
, si el aro se mueve uniformemente con una velocidad ![]() y gira con una velocidad angular
y gira con una velocidad angular ![]() en torno al eje que pasa por el centro.
en torno al eje que pasa por el centro.
Solución:
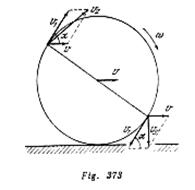
Dividamos todo el aro en secciones pequeños e iguales de masa ![]() cada una. Analicemos dos secciones simétricas (con relación al centro).Todas las partículas del aro participan simultáneamente en dos movimientos: en el movimiento de avance con velocidad
cada una. Analicemos dos secciones simétricas (con relación al centro).Todas las partículas del aro participan simultáneamente en dos movimientos: en el movimiento de avance con velocidad ![]() y en el movimiento de rotación con velocidad
y en el movimiento de rotación con velocidad ![]() . La velocidad resultante
. La velocidad resultante ![]() de la sección superior del aro se determina como la suma geométrica de las velocidades
de la sección superior del aro se determina como la suma geométrica de las velocidades ![]() y
y ![]() (fig. 373):
(fig. 373):
![]()
Para la sección simétrica tenemos
![]()
La energía cinética resultante de ambas secciones es
![]()
Como la expresión es válida para cualquier una de las dos secciones, podemos escribir para todo el aro que
![]()
Si el aro rueda sin deslizamiento, entonces ![]() y por lo tanto
y por lo tanto ![]()
Determinar la energía cinética de la oruga de un tractor que se mueve con una velocidad ![]() . La distancia entre los ejes de las ruedas sobre las cuales está la oruga es igual a
. La distancia entre los ejes de las ruedas sobre las cuales está la oruga es igual a ![]() ; el radio de las ruedas es
; el radio de las ruedas es![]() . La unidad de la longitud de la oruga pesa
. La unidad de la longitud de la oruga pesa ![]() .
.
Solución:
![]()
Solución:
El cilindro de material más denso evidentemente será el hueco. Para velocidades iguales del movimiento de avance, la energía cinética del movimiento de rotación será mayor en el cilindro hueco, porque las partículas de su masa se encuentran más alejadas del centro y, por lo tanto, tienen mayores velocidades. Debido a ello, en el proceso de rodadura sin deslizar de un plano inclinado el cilindro hueco adquiere una velocidad menor que el cilindro sólido. Las energías cinéticas totales de ambos cilindros al final del trayecto serán iguales, lo que es posible sólo para diferentes velocidades, porque para velocidades iguales las energías del movimiento de avance serán iguales y la energía del movimiento de rotación del cilindro sólido será obligatoriamente menor que la del cilindro hueco.
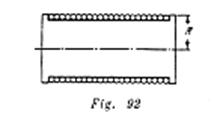
En una bobina de radio ![]() fue arrollado uniformemente un cable flexible (fig. 92). El peso de la unidad de longitud del cable es
fue arrollado uniformemente un cable flexible (fig. 92). El peso de la unidad de longitud del cable es![]() . El peso de todo el cable es
. El peso de todo el cable es![]() . La bobina se mueve sin deslizamiento por inercia a lo largo de un plano horizontal. El cable se desenrolla y queda en el plano. Inicialmente, cuando todo el cable estaba arrollado en la bobina, la velocidad del centro de la bobina era igual a
. La bobina se mueve sin deslizamiento por inercia a lo largo de un plano horizontal. El cable se desenrolla y queda en el plano. Inicialmente, cuando todo el cable estaba arrollado en la bobina, la velocidad del centro de la bobina era igual a ![]() . Prescindiendo del radio de la sección transversal del cable (en comparación con
. Prescindiendo del radio de la sección transversal del cable (en comparación con ![]() ) y de la masa de la propia bobina, calcular la velocidad del centro de la bobina en el momento cuando se encuentre en el plano una parte del cable de longitud
) y de la masa de la propia bobina, calcular la velocidad del centro de la bobina en el momento cuando se encuentre en el plano una parte del cable de longitud ![]() . ¿Bajo la acción de qué fuerza varía la cantidad de movimiento del cable?
. ¿Bajo la acción de qué fuerza varía la cantidad de movimiento del cable?
Solución:
En el movimiento de la bobina la fuerza de rozamiento no realiza trabajo, porque no existe deslizamiento del cable y de la bobina. Por lo tanto, la energía del sistema no cambia y es
![]()
donde ![]() es la velocidad que buscamos. De la ecuación obtenemos que
es la velocidad que buscamos. De la ecuación obtenemos que![]() que tiende al infinito cuando
que tiende al infinito cuando ![]() , porque no tenemos en consideración la masa de la bobina. La cantidad de movimiento se disminuye gracias a la acción de la fuerza de rozamiento dirigida en sentido opuesto al del movimiento.
, porque no tenemos en consideración la masa de la bobina. La cantidad de movimiento se disminuye gracias a la acción de la fuerza de rozamiento dirigida en sentido opuesto al del movimiento.
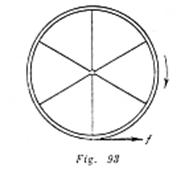
Sobre una polea de radio ![]() que gira en torno de un eje fijo actúa la fuerza de fricción
que gira en torno de un eje fijo actúa la fuerza de fricción ![]() (fig. 93). Determinar la variación de la velocidad angular de la polea en función del tiempo, si en el momento inicial la velocidad angular es igual a
(fig. 93). Determinar la variación de la velocidad angular de la polea en función del tiempo, si en el momento inicial la velocidad angular es igual a ![]() . La masa de la polea es
. La masa de la polea es ![]() , la masa de los rayos puede ser despreciada.
, la masa de los rayos puede ser despreciada.
Solución:
Como la fuerza de rozamiento es constante, el movimiento será uniformemente retardado. La potencia desarrollada por la fuerza de rozamiento es igual a ![]() , donde
, donde ![]() es la velocidad instantánea del punto de la polea, al cual fue aplicada la fuerza
es la velocidad instantánea del punto de la polea, al cual fue aplicada la fuerza ![]() . El trabajo en un tiempo
. El trabajo en un tiempo ![]() es igual a la potencia media multiplicada por el tiempo
es igual a la potencia media multiplicada por el tiempo ![]() :
:
![]()
El cambio de la energía cinética de la polea es igual a este trabajo:
![]()
De ahí ![]()
Un aro de radio ![]() que gira con velocidad angular
que gira con velocidad angular![]() , fue colocado en una superficie horizontal áspera. Determinar la velocidad
, fue colocado en una superficie horizontal áspera. Determinar la velocidad ![]() del centro del aro después de terminar el deslizamiento. En el momento inicial la velocidad del centro del aro era nula.
del centro del aro después de terminar el deslizamiento. En el momento inicial la velocidad del centro del aro era nula.
Solución:
Como la fuerza de rozamiento ![]() es constante, la variación de la cantidad de movimiento del aro en un tiempo
es constante, la variación de la cantidad de movimiento del aro en un tiempo ![]() será igual a
será igual a ![]() . En caso de rodadura sin deslizar, la velocidad del punto del aro, al cual fue aplicada la fuerza de rozamiento, es nula. Igualando al trabajo de las fuerzas de rozamiento a la diferencia de las energías cinéticas, obtenemos que
. En caso de rodadura sin deslizar, la velocidad del punto del aro, al cual fue aplicada la fuerza de rozamiento, es nula. Igualando al trabajo de las fuerzas de rozamiento a la diferencia de las energías cinéticas, obtenemos que
![]()
(Véase el problema 215). Resolviendo la ecuación respecto a ![]() hallamos que .
hallamos que .
![]()
A un aro de radio ![]() , colocado en un plano horizontal áspero, fue transmitida en dirección horizontal una velocidad de avance
, colocado en un plano horizontal áspero, fue transmitida en dirección horizontal una velocidad de avance ![]() . Determinar la velocidad angular
. Determinar la velocidad angular ![]() de rotación del aro, después de haber terminado el deslizamiento de éste.
de rotación del aro, después de haber terminado el deslizamiento de éste.
Solución:
Las ecuaciones que expresan la variación de la cantidad de movimiento y la variación de la energía cinética del aro, tiene la forma:
![]()
Donde ![]() es la velocidad del centro del aro durante la rodadura sin deslizar. Resolviendo estas ecuaciones con relación a
es la velocidad del centro del aro durante la rodadura sin deslizar. Resolviendo estas ecuaciones con relación a ![]() , obtenemos que
, obtenemos que ![]() . Por consiguiente, el valor que buscamos es
. Por consiguiente, el valor que buscamos es ![]()
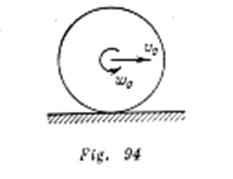
Un aro de radio ![]() que gira con velocidad angular
que gira con velocidad angular ![]() fue colocado en un plano horizontal áspero. Al aro fue transmitida una velocidad de avance
fue colocado en un plano horizontal áspero. Al aro fue transmitida una velocidad de avance ![]() (fig. 94).
(fig. 94).
Considerando que la fuerza de fricción de deslizamiento es igual a ![]() , determinar el carácter del movimiento del aro.
, determinar el carácter del movimiento del aro.
Solución:
Las ecuaciones que expresan la variación de la cantidad de movimiento y la variación de la energía cinética del aro, tienen la forma:
![]()
![]()
Donde ![]() es la velocidad del centro del aro en cualquier momento de tiempo ulterior. Resolviendo el sistema de ecuaciones dado, hallamos que
es la velocidad del centro del aro en cualquier momento de tiempo ulterior. Resolviendo el sistema de ecuaciones dado, hallamos que
![]()
Si ![]() , en el momento de tiempo
, en el momento de tiempo ![]() el aro para girando con velocidad angular
el aro para girando con velocidad angular![]() . Luego el aro comienza a moverse en sentido contrario con deslizamiento. Al pasar un tiempo el deslizamiento cesa y el aro rodará sin deslizamiento hacia la izquierda con velocidad de traslación
. Luego el aro comienza a moverse en sentido contrario con deslizamiento. Al pasar un tiempo el deslizamiento cesa y el aro rodará sin deslizamiento hacia la izquierda con velocidad de traslación ![]()
(Véase el problema 221).
Si ![]() , entonces, transcurrido un tiempo
, entonces, transcurrido un tiempo ![]() , el aro deja girar, moviéndose hacia la derecha con velocidad de traslación
, el aro deja girar, moviéndose hacia la derecha con velocidad de traslación ![]() . Posteriormente, la rotación del aro se realizará en sentido contrario y, pasado un tiempo, el aro rodará sin deslizamiento hacia la derecha; la velocidad angular será
. Posteriormente, la rotación del aro se realizará en sentido contrario y, pasado un tiempo, el aro rodará sin deslizamiento hacia la derecha; la velocidad angular será ![]() . Subrayamos, como muestra la experiencia, que el aro frenará inclusive en la ausencia del deslizamiento. Nosotros no obtenemos tal resultado, porque no tenemos en consideración la fricción por rodadura.
. Subrayamos, como muestra la experiencia, que el aro frenará inclusive en la ausencia del deslizamiento. Nosotros no obtenemos tal resultado, porque no tenemos en consideración la fricción por rodadura.
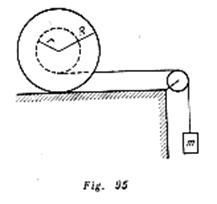
Un tubo cilíndrico de radio ![]() está unido, por los rayos, a dos aros de radio
está unido, por los rayos, a dos aros de radio ![]() . La masa de ambos aros es igual a
. La masa de ambos aros es igual a ![]() . La masa del tubo y de los rayos en comparación con la masa de los aros
. La masa del tubo y de los rayos en comparación con la masa de los aros ![]() , puede ser menospreciada.
, puede ser menospreciada.
En el tubo fue arrollado un hilo que se apoya sobre una polea imponderable. Un peso de masa ![]() (fig. 95) fue atado al extremo del hilo. Encontrar la aceleración del peso, la tensión del hilo y la fuerza de fricción entre los aros y el plano. (Considerar que los aros no se deslizan.) Determinar para qué valores del coeficiente de fricción los aros se deslizarán.
(fig. 95) fue atado al extremo del hilo. Encontrar la aceleración del peso, la tensión del hilo y la fuerza de fricción entre los aros y el plano. (Considerar que los aros no se deslizan.) Determinar para qué valores del coeficiente de fricción los aros se deslizarán.
Solución:
Como los aros no deslizan, entonces ![]() , que es la velocidad del centro de gravedad de los aros, y
, que es la velocidad del centro de gravedad de los aros, y ![]() que la velocidad del paso, se relaciona como
que la velocidad del paso, se relaciona como ![]() .
.
Supongamos que el peso descienda a una altura ![]() . Considerando que en el momento inicial el sistema estaba en reposo y valiéndose del principio de conservación de la energía, podemos escribir que
. Considerando que en el momento inicial el sistema estaba en reposo y valiéndose del principio de conservación de la energía, podemos escribir que
![]()
(Véase el problema 215).
De la última relación hallamos la velocidad del peso:
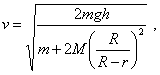
Y determinamos la aceleración del peso que es igual a
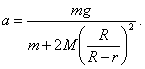
El peso se mueve hacia abajo con aceleración a bajo la acción de dos fuerzas: la fuerza de gravedad ![]() y la de tensión del hilo
y la de tensión del hilo ![]() . La tensión del hilo que buscamos es:
. La tensión del hilo que buscamos es:
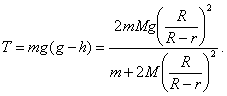
Como el centro de gravedad del aro se mueve con aceleración ![]() , bajo la acción de la fuerza
, bajo la acción de la fuerza ![]() y de la fuerza de fricción
y de la fuerza de fricción ![]() , entonces, basándose en la segunda ley de Newton, para la fuerza
, entonces, basándose en la segunda ley de Newton, para la fuerza ![]() obtenemos la igualdad
obtenemos la igualdad
![]()
o
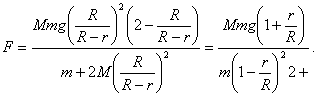
El valor de la fuerza de fricción no puede superar el valor ![]() . Como resultado de esto, el deslizamiento comenzará cuando
. Como resultado de esto, el deslizamiento comenzará cuando
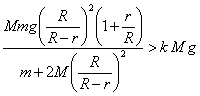
o
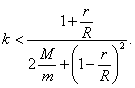
Sobre un plano inclinado está situada una bobina. En la bobina fue devanado un hilo apoyado sobre una polea imponderable y en cuyo extremo libre está atado un peso de masa![]() (fig. 96). Se supone que la masa de la bobina
(fig. 96). Se supone que la masa de la bobina ![]() está distribuida uniformemente por la circunferencia de radio
está distribuida uniformemente por la circunferencia de radio ![]() . No hay fricción. Determinar para qué valor del ángulo de inclinación
. No hay fricción. Determinar para qué valor del ángulo de inclinación ![]() el centro de gravedad de la bobina estará en reposo.
el centro de gravedad de la bobina estará en reposo.
Solución:
El centro de gravedad de la bobina no se desplazará si la tensión del hilo satisface la igualdad ![]() . Para determinar la tensión del hilo
. Para determinar la tensión del hilo ![]() , determinamos primeramente la aceleración del peso de masa
, determinamos primeramente la aceleración del peso de masa ![]() . Supongamos que el peso descienda a una altura
. Supongamos que el peso descienda a una altura ![]() . Como el centro de gravedad de la bobina, por la condición del problema, deberá mantenerse en reposo, entonces la variación de la energía potencial es igual a
. Como el centro de gravedad de la bobina, por la condición del problema, deberá mantenerse en reposo, entonces la variación de la energía potencial es igual a ![]() . Si
. Si ![]() es la velocidad del movimiento del peso de masa
es la velocidad del movimiento del peso de masa ![]() , entonces la velocidad de los puntos de la bobina que se encuentran a una distancia
, entonces la velocidad de los puntos de la bobina que se encuentran a una distancia ![]() del eje de rotación es
del eje de rotación es ![]() . Por consiguiente, la energía cinética del sistema es
. Por consiguiente, la energía cinética del sistema es
![]()
Del principio de conservación de la energía deducimos que
![]()
De esta ecuación obtenemos que la aceleración del peso es ![]() . Conociendo la aceleración del peso, encontramos la tensión del hilo
. Conociendo la aceleración del peso, encontramos la tensión del hilo
![]()
De este modo para ![]() obtenemos la siguiente expresión:
obtenemos la siguiente expresión:
![]()
El centro de gravedad de la bobina estará en reposo sólo cuando
![]()
Una tabla de masa ![]() fue colocada sobre dos rodillos cilíndricos iguales, de radio
fue colocada sobre dos rodillos cilíndricos iguales, de radio ![]() . Los rodillos se encuentran en un plano horizontal. En el momento inicial el sistema estaba en reposo. Luego a la tabla le aplicaron una fuerza
. Los rodillos se encuentran en un plano horizontal. En el momento inicial el sistema estaba en reposo. Luego a la tabla le aplicaron una fuerza ![]() en dirección horizontal. Hallar la aceleración de la tabla, el valor de las fuerzas de rozamiento entre los rodillos y la tabla, así como entre los rodillos y el plano horizontal. Considerar que no existe deslizamiento. Los rodillos tienen la forma de dos barras cilíndricas de paredes de masa
en dirección horizontal. Hallar la aceleración de la tabla, el valor de las fuerzas de rozamiento entre los rodillos y la tabla, así como entre los rodillos y el plano horizontal. Considerar que no existe deslizamiento. Los rodillos tienen la forma de dos barras cilíndricas de paredes de masa ![]() cada una.
cada una.
Solución:
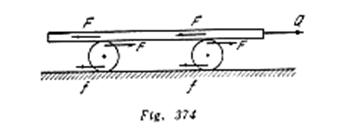
Si la velocidad de la tabla es igual a![]() , la velocidad del centro de gravedad de cada rodillo es
, la velocidad del centro de gravedad de cada rodillo es ![]() (véase el problema 57). La energía cinética del sistema (tabla y ambos rodillos) será igual a
(véase el problema 57). La energía cinética del sistema (tabla y ambos rodillos) será igual a
![]()
Igualando la energía cinética al trabajo de la fuerza ![]() en el trayecto
en el trayecto ![]() , obtenemos que
, obtenemos que
![]()
(fig. 374). (Las fuerzas de fricción no realizan trabajo porque no existe deslizamiento).
De la expresión para la velocidad del movimiento de la tabla deducimos que su aceleración es ![]() . Para determinar la fuerza de fricción con que el rodillo actúa sobre la tabla, escribimos la ecuación de movimiento de la tabla:
. Para determinar la fuerza de fricción con que el rodillo actúa sobre la tabla, escribimos la ecuación de movimiento de la tabla:
![]() . Sustituyendo el valor de la aceleración
. Sustituyendo el valor de la aceleración ![]() en esta ecuación, obtenemos que
en esta ecuación, obtenemos que ![]() .
.
Como la velocidad del centro de gravedad del rodillo es dos veces menor que la velocidad de la tabla, entonces la aceleración del centro de gravedad del rodillo será dos veces menor que la aceleración de la tabla. Debido a ello la ecuación de movimiento del centro de gravedad del rodillo tendrá la siguiente forma: ![]() . De esta ecuación se deduce que
. De esta ecuación se deduce que ![]() .
.
Una polea de dos etapas se compone de dos aros finos, rígidamente unidos entre sí, cuyos radios son R y r, y las masas ![]() y
y ![]() , respectivamente. En cada una de las etapas de la misma se devanan hilos, en cuyos extremos se colocan pesos de masa
, respectivamente. En cada una de las etapas de la misma se devanan hilos, en cuyos extremos se colocan pesos de masa ![]() y
y ![]() (fig. 97). Hallar la aceleración de los pesos
(fig. 97). Hallar la aceleración de los pesos ![]() y
y ![]() , la tensión de los hilos y la fuerza con que el sistema actúa sobre el eje de la polea.
, la tensión de los hilos y la fuerza con que el sistema actúa sobre el eje de la polea.
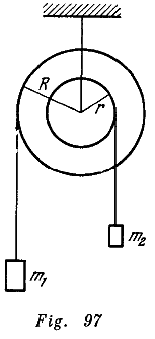
Solución:
Supongamos para mayor precisión que ![]() En este caso, el primer peso bajará y el segundo se elevará. Supongamos que el primer peso baje a una altura h. Entonces el segundo sube a
En este caso, el primer peso bajará y el segundo se elevará. Supongamos que el primer peso baje a una altura h. Entonces el segundo sube a ![]() . De modo, la pérdida de la energía potencial será
. De modo, la pérdida de la energía potencial será
![]()
Si el valor absoluto de la velocidad del primer peso es v, entonces la velocidad del segundo será ![]() . Todos los puntos de la primera etapa de la polea tienen velocidades v y todos los puntos de la segunda etapa poseen una velocidad
. Todos los puntos de la primera etapa de la polea tienen velocidades v y todos los puntos de la segunda etapa poseen una velocidad ![]() . La energía cinética del sistema será igual a
. La energía cinética del sistema será igual a
![]()
Del principio de conservación de la energía deducimos que
![]()
O
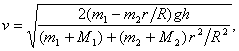
De donde hallamos la aceleración del primer peso
![]()
De la relación ![]() , donde
, donde![]() es la aceleración del segundo peso, determinamos
es la aceleración del segundo peso, determinamos
![]()
Las tensiones de los hilos![]() y
y ![]() , basándose en la segunda ley de Newton, son
, basándose en la segunda ley de Newton, son
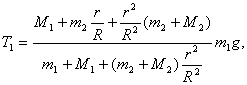

La fuerza F con que el sistema actúa sobre el eje de la polea, es
![]()
Un cilindro de paredes delgadas y homogéneo de radio R y de masa M baja rodando sin deslizamiento, bajo la acción de la fuerza de la gravedad, de un plano inclinado que forma un ángulo α con la horizontal. Valiéndose del principio de conservación de la energía, determinar: 1) la velocidad del centro de gravedad y la velocidad angular de rotación del cilindro, transcurrido el tiempo t desde el inicio del movimiento. (Se supone que el cilindro en el momento inicial se encuentra en reposo); 2) la aceleración del centro de gravedad del cilindro.
Solución:
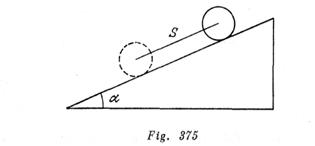
Supongamos que el trayecto recorrido por el centro de gravedad del cilindro, en un tiempo t, sea S, y la velocidad del centro de gravedad, en este momento de tiempo sea igual a v. (fig. 375). Basándose en el principio de la conservación de la energía, podemos escribir que
![]()
de donde la velocidad es ![]() y por lo tanto, la aceleración es
y por lo tanto, la aceleración es ![]() La velocidad del centro de gravedad del cilindro y la velocidad angular de rotación del mismo serán, respectivamente,
La velocidad del centro de gravedad del cilindro y la velocidad angular de rotación del mismo serán, respectivamente,![]() y
y![]() .
.
