Ejercicios – Mecánica – Ley de Gravitación Universal

Encontrar la magnitud y la dimensión en el sistema CGS de la constante de gravitación universal, tomando en consideración que el radio medio de la Tierra es y la masa de la Tierra,

Solución:

La aceleración es (véase el problema 228). Tomando , encontramos que

¿En que condiciones los cuerpos dentro de una nave cósmica están en estado de imponderabilidad, es decir, dejaran de ejercer presión sobre las paredes de la cabina de la nave?

Solución:

Los cuerpos dentro de una nave cósmica no ejercen presión sobre sus paredes si estos tienen una aceleración igual a la aceleración de la nave cósmica. La misma aceleración en la región del espacio dada, puede trasmitirse a todos los cuerpos independientemente de sus masas, solo por la fuerza gravitacional. Por consiguiente es necesario que el motor de la nave este desconectado y que no exista resistencia del medio exterior.

La nave puede moverse en cualquier dirección respecto a la dirección de las fuerzas gravitacionales.

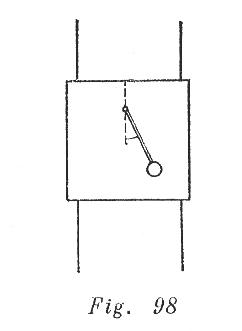
Un péndulo simple, que consta de una barra y un disco (fig. 98), esta sujeto a un cuadro de madera que puede caer libremente a lo largo de los alambres que lo dirigen. El péndulo se inclino de la posición de equilibrio, en un ángulo , y luego se soltó. En

el momento, en que el péndulo pasaba por la posición mas inferior, se dejo de sostener el cuadro, entonces este comienza a caer libremente.¿Como se moverá el péndulo con relación al cuadro?. La fricción y la resistencia del aire pueden despreciarse

Solución:

La fuerza de gravedad trasmite la misma aceleración al péndulo y al cuadro. En el sistema no surge ninguna deformación durante la caída libre provocada por la gravitación. Por eso el péndulo se moverá respecto al cuadro como si no existiera la gravitación (véase la resolución del problema 230). El cuadro girara con velocidad angular constante hasta que dure la caída del cuadro.

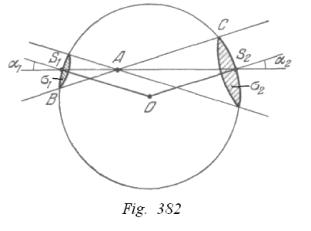
Un planeta se mueve por una elipse, en cuyo foco se encuentra el sol. Teniendo en cuenta el trabajo de la fuerza de gravitación, indicar ¿en que punto de la trayectoria la velocidad del planeta será máxima y en que punto será mínima?

Solución:

En la sección BCA (fig. 376) la fuerza de gravitación realiza un trabajo positivo (el ángulo es agudo) y, por lo tanto, la velocidad del planeta aumenta. En el punto A la velocidad alcanza su valor máximo. En la sección ADB la fuerza de gravitación realiza un trabajo negativo (el ángulo es obtuso), por consiguiente en el movimiento por esta sección la velocidad del planeta se disminuye, alcanzando su valor mínimo en el punto B.

Un satélite artificial de la tierra se mueve a una altura h=670km. Por una orbita circular. Encontrarla velocidad del movimiento del satélite.

Solución:

A fin de que el satélite se mueva por una orbita cerrada (circunferencia de radio ) sobre el debe actuar una fuerza dirigida al centro. En el caso dado esta fuerza es la de atracción de la tierra. Por la segunda ley de newton tenemos que

,

Donde M es la masa de la tierra; R=6370km, el radio del globo terráqueo;, la constante gravitacional. En la superficie de la tierra, tenemos por lo tanto,

¿Como varía, en función del tiempo, la velocidad de un satélite artificial de la Tierra que se mueve en las capas atmosféricas superiores?

Solución:

Bajo la influencia de la resistencia atmosférica, el satélite, en el correr del tiempo, se aproxima paulatinamente a la tierra. El radio de su orbita disminuye. Como en las capas superiores la resistencia es pequeña, la disminución del radio durante una vuelta es insignificante. Considerando la orbita aproximadamente circular podemos escribir que

,

Donde R es el radio de la orbita. Recibimos que , es decir, la velocidad del satélite aumenta con la disminución e R. este resultado puede explicarse de la siguiente manera.

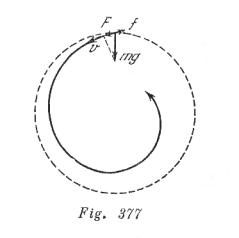
Como consecuencia de la resistencia atmosférica el movimiento del satélite lanzado, por ejemplo, a una orbita circular (línea punteada en la figura 377) Se realizara en realidad según una cierta espiral (línea llena en la figura 3.77). Gracias a esto, la proyección de la fuerza de gravitación F en la dirección de la velocidad del satélite V es diferente de cero. Precisamente el trabajo de la fuerza F (la fuerza F es mayor que la fuerza de resistencia de la atmósfera f) aumentara la velocidad.

Al moverse en la atmósfera, la energía mecánica total del satélite se disminuye, sin embargo la energía potencial al aproximarse a la tierra, se disminuye mas rápidamente que la energía total. Por eso la energía cinética aumenta. Es conveniente subrayar que en las capas atmosféricas densas, debido a la fuerza de resistencia grande, no podemos ni aproximadamente considerar el movimiento del satélite como giratorio por una circunferencia y, por consiguiente, nuestra conclusión no es valida.

Por una órbita circular, a una distancia no muy grande el uno del otro y en la misma dirección, vuelan dos satélites. Del primer satélite es necesario lanzar para el segundo un contenedor. ¿En qué caso el contenedor alcanzará con más rapidez el segundo satélite: si lanzarlo en sentido del movimiento del primer satélite o en sentido opuesto al sentido del movimiento del mismo? La velocidad del contenedor respecto al satélite es U y es mucho menor que la velocidad del satélite V.

Solución:

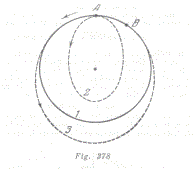
Si lanzamos el contenedor en sentido opuesto al movimiento del satélite A, entonces este último se moverá según una elipse 2, situada dentro de la órbita del satélite (fig. 378). El periodo de rotación del contenedor será mucho menor que el período de rotación del satélite B y como consecuencia de esto, ellos podrán encontrarse en el punto de contacto de las órbitas solamente después de que los satélites realicen el gran número de vueltas. El contenedor deberá se lanzado en sentido del movimiento del satélite A. el comenzará el movimiento según la elipse 3.

Es necesario escoger la velocidad u de modo que en una vuelta del contenedor el satélite B también realice una vuelta y recorra adicionalmente el trayecto AB. Esto es realmente posible, ya que el período de rotación por la elipse 3 es varias veces mayor que el período de rotación por la órbita circular 1. El contenedor se encontrará con el satélite en el punto de contacto de las órbitas 3 y 1.

Valorar la masa del Sol M, conociendo el radio medio de la órbita de la Tierra.

Solución:

Considerando la órbita de la Tierra aproximadamente circular, para la fuerza de gravitación podemos escribir la expresión:

, donde m es la masa de la Tierra y , la velocidad angular de la Tierra ( días). Por otro lado, de acuerdo con la ley de atracción universal , donde M es la masa del Sol, recibimos que

o

Determinar la distancia mínima h de la superficie de la Tierra del primer satélite artificial de ella, lanzado en la URSS el 4 de octubre de 1957, si se conocen los parámetros siguientes: la distancia máxima del satélite con relación a la Tierra H=900 Km.; el período de rotación del satélite alrededor de la Tierra T=96min; el semieje mayor de la órbita lunar R = 384.400 Km.; el período de movimiento de la luna alrededor de la Tierra T =27.3 días y el radio de la Tierra

Solución:

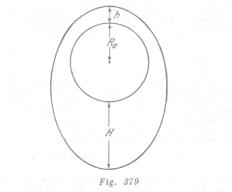
Como la Luna y el satélite se mueven en el campo gravitacional de la Tierra, aplicamos, la tercera ley de Kepler, o sea,

(fig. 379), de donde

En el agua hay una burbuja de aire de radio r y una bola de hierro del mismo radio. ¿Se atraerán o se repelerán la burbuja y la bola? ¿Cuál será el valor de la fuerza de interacción entre ellas? La distancia entre los centros de la bola y la burbuja es igual a R.

Solución:

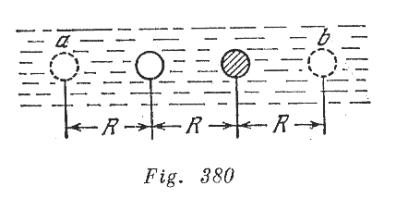
Como la masa de la bola, en el mismo volumen, es mayor que la masa del agua, entonces el campo gravitacional es mayor cerca de la bola que lejos de ella. De modo análogo, el agua en las proximidades de la bola esta mas comprimida. La fuerza de presión del liquido que actúa sobre la burbuja del lado izquierdo será un tanto menor que la fuerza que actúa sobre la burbuja del lado derecho. Por otra parte, la fuerza de gravitación entre el aire en la burbuja y la bola es mayor que la fuerza de atracción entre el aire y el volumen de agua mostrado con el punteado (volumen a en la figura 380). Como la masa de aire en la burbuja es muy pequeña, resulta ser decisiva la acción del primer factor. La burbuja se repelerá de la bola.

El movimiento de la bola de hierro, al contrario, se determinará por el hecho de que la fuerza de atracción entre el aire en la burbuja y la bola es mucho menor que la fuerza de atracción entre la bola y el volumen de agua marcado con la línea punteada (figura 380, volumen b). El cálculo de la fuerza se hace por medio de las siguientes consideraciones. En un medio homogéneo (agua) existe una esfera que carece casi por completo de masa (burbuja) y una esfera con masa excesiva (bola). Formalmente esto puede analizarse como la presencia de masas positiva y negativa.

La fuerza de interacción entre las esferas en el liquido es igual a la fuerza de interacción en el vació entre una masa negativa, igual a masa de agua en el volumen de la burbuja, y una masa positiva, igual a la diferencia entre la masa de la bola de hierro y la masa de agua en el mismo volumen. Por lo tanto tenemos que , donde es la masa de agua en la esfera de radio r y , la masa de la bola de hierro.

En el agua hay dos burbujas de aire de radio r. ¿Habrá atracción o repulsión entre ellas? ¿Cuál es el valor de la fuerza de interacción? La distancia entre las burbujas es R.

Solución:

En las cercanías de la burbuja el campo gravitacional es menor que en un liquido homogéneo. Por consiguiente, allí el líquido es menos comprimido. Por eso, una burbuja tiende al sector líquido, donde existe otra burbuja e inversamente. Las burbujas se atraerán. Dos burbujas en un líquido homogéneo, cuyas masas son insignificantes, pueden considerarse formalmente con masas negativas sobrepuestas en una masa positiva m del medio en el volumen de la burbuja:

.

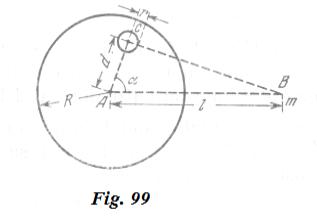
Una esfera de plomo de radio tiene, dentro de si misma, una cavidad esférica de radio , cuyo centro se encuentra a una distancia del centro de la esfera (fig. 99). ¿Con qué fuerza la esfera atraerá un punto material de masa , que se encuentra a una distancia del centro de la esfera, si la línea que une los centros de la esfera y de la cavidad, forma un ángulo con la línea que une al centro de la esfera con el punto material?

Solución:

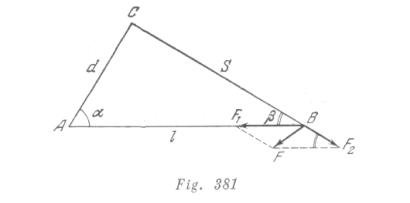
Si la esfera fuera sólida, entonces la fuerza gravitacional será igual a , donde era la masa de la esfera sin la cavidad. La presencia de la cavidad es equivalente al surgimiento de la fuerza de repulsión , donde siendo S la distancia entre el centro de la cavidad y el punto material

La fuerza F que buscamos es la suma geométrica de las fuerzas y (fig. 381). Aplicándole teorema de los cósenos, recibimos que

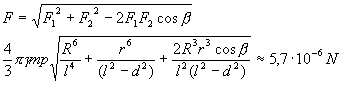
Un cuerpo, cuyas dimensiones pueden menospreciarse, fue colocado dentro de una esfera homogénea y de pared delgada. Demostrar que la fuerza de atracción con que actúa la esfera sobre el cuerpo es igual a cero para cualquier posición del cuerpo dentro de la esfera.

Solución:

La fuerza de atracción que buscamos será la suma geométrica de las fuerzas de atracción creadas por las diferentes secciones de la esfera. Las secciones pequeñas y (fig. 382) se cortan de la esfera en forma de conos con vértice en el punto A que se obtienen girando la generatriz alrededor del eje . Las áreas de las secciones son iguales a y , y sus masas a y , respectivamente, donde es el ángulo sólido, bajo el cual se ven ambas secciones desde el punto A; es la densidad superficial de la esfera (la masa por unidad de área); , porque el triángulo es isósceles. Las fuerzas de atracción creadas por las secciones, son iguales a

=;

=,

Respectivamente, donde m es la masa del cuerpo, y están dirigidas en sentidos opuestos. La resultante de las masas es nula. Al examinar de modo análogo otras secciones correspondientes de la esfera, nos convencemos de que todas ellas, de dos en dos, se compensan mutuamente. Por consiguiente, la fuerza de atracción que actúa por parte de la esfera sobre el cuerpo situado dentro de la esfera, es igual a cero. Subrayamos que este resultado es válido también para una esfera de espesor finito, porque ésta puede ser dividida en cualquier cantidad de capas esféricas finas, para cada una de las cuales es válida la demostración hecha arriba.

¿Con qué fuerza el centro de la Tierra atrae un cuerpo de masa m que se encuentra en un pozo profundo si la distancia del cuerpo al centro de la tierra es igual a ? La densidad de la tierra debe ser considerada como única en todos los puntos e igual a .

Solución:

La fuerza de atracción es igual a la fuerza con que el cuerpo de masa m se atrae a la esfera de radio r y densidad p. Las capas espesas exteriores de la tierra no ejercen, como fue demostrado en el problema 241, influencia alguna en el cuerpo. Por eso la fuerza que buscamos será

Esta fuerza disminuye proporcionalmente ara medida que se aproxima al centro de la tierra.

En un vaso de agua flota, en posición vertical, un trozo de madera. ¿Cómo variará el nivel del agua en el vaso si el trozo de madera toma la posición horizontal?

Solución:

El nivel del agua no cambiará, porque la cantidad de agua desplazada continuará la misma.

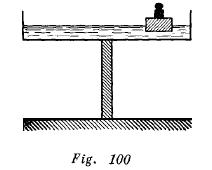
Un recipiente de agua fue colocado en el extremo de una tabla (fig. 100) ¿Perderá el equilibrio la tabla si sobre la superficie del agua se coloca un trozo de madera y sobre este último, un peso de modo que ambos floten en la superficie del agua?

Solución:

El equilibrio no se alterará, puesto que, de acuerdo con la ley de Pascal, la presión sobre el fondo del recipiente será igual en todos los lugares.

En un vaso de agua flota un pedazo de hielo. ¿Cómo cambia el nivel del agua en el vaso cuando el hielo se derrite? Analizar los siguientes casos:

í) el hielo es completamente homogéneo;

2) en el hielo se encuentra una piedra fuertemente adherida;

3) dentro del pedazo de hielo hay una burbuja de aire.

Solución:

1) Como el pedazo de hielo flota, el peso de toda el agua desplazada por éste es igual al peso del propio hielo o del agua recibida de éste. Por eso el agua que se forma después del deshielo ocupará un volumen igual al volumen de la parte hundida del pedazo de hielo y por consiguiente el nivel del agua no cambiará.

2) El volumen de la parte sumergida del pedazo de hielo con la piedra es mayor que la suma de los volúmenes de la piedra y el agua que se obtiene después del deshielo. Por lo tanto, el nivel del agua en el copo se descenderá.

3) El peso del agua desplazada es igual al peso del hielo (el peso del aire en la burbuja puede prescindirse). Por eso igualmente como en el caso 1), el nivel del agua no cambiará.

Un cuerpo homogéneo y compacto, colocado en un líquido con peso específico , pesa ; y colocado en un líquido con peso específico , pesa . De­
terminar el peso específico del cuerpo.

Solución:

El peso del cuerpo hundido en el líquido en el primer caso es igual a ; en el segundo caso es igual a, donde es el volumen del cuerpo; de ahí resulta que

En el centro de un lago grande congelado han hecho un claro. El grosor del hielo resultó igual a . ¿De qué longitud será necesaria la cuerda para sacar un balde de agua?

Solución:

falta la respuesta aqui

En una taza con agua flota una cajita de cerillas dentro de la cual hay una piedra pequeña. ¿Variará el nivel del agua en la taza si la piedra se saca de la cajita y se pone en el agua?

Solución:

Al retirar la piedra, la caja se hizo más ligera en un peso igual al de la piedra y, por lo tanto, el volumen del agua desplazada por la caja disminuyó en , donde es el peso de la piedra y el peso específico del agua. Al sumergirse en el agua, la piedra desalojará un volumen de agua igual a su propio volumen, o sea,, donde es el peso específico de la sustancia de la piedra. Como , entonces y por consiguiente el nivel del agua en la taza disminuirá.

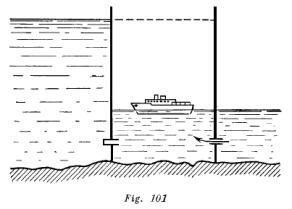
Un buque atraviesa una esclusa elevándose hasta el mayor nivel en la cámara de la misma, adonde el agua se bombea por la parte del nivel inferior (fig. 101). ¿En qué caso las bombas realizan mayor trabajo: cuando en la cámara se encuentra un buque grande o un navío pequeño?

Solución:

En ambos casos el trabajo de las bombas es igual, porque la misma cantidad de agua bombeada sube a la misma altura.

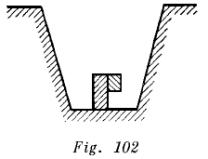
De dos láminas homogéneas y del mismo grosor, con pesos específicos de y , fueron corta­dos un cuadrado de lado a y un rectángulo de lados a y , siendo el cuadrado cortado del material más pesado. El cuadrado y el rectángulo fueron unidos en forma y colocados en el fondo de un vacío (fig. 102). ¿Qué pasará si llenamos el recipiente de agua?

Solución:

Una figura en forma de T está en una posición estable, en el fondo de un recipiente vacío, porque la perpendicular trazada del centro de gravedad de la figura no sale de los límites del área de la base. A medida que vertemos agua en el recipiente comienza a aumentar la fuerza de empuje que actúa sobre el rectángulo (se supone que el agua tiene la posibilidad de pasar por debajo de la figura). Para una profundidad de agua en el recipiente igual a 0,5 a, la suma de los momentos de las fuerzas que tienden a girar el cuerpo en sentido horario, será igual a la suma de los momentos de las fuerzas que tienden a girar el cuerpo en sentido antihorario. Si continuamos llenando el recipiente de agua, la figura caerá.

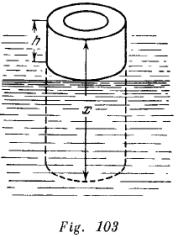
Un tubo flota en el agua en posición vertical (fig. 103). La altura del tubo que sobresale del agua es Dentro del tubo se invierte aceite de peso específico ¿Cuál deberá ser la longitud del tubo para llenarlo totalmente de aceite?

Solución:

La longitud del tubo se halla de la condición que expresa la igualdad de las presiones en la profundidad del extremo inferior del tubo. Aquí es el peso específico del agua. Obtenemos, entonces, que = 50 cm.

Un émbolo de peso tiene la forma de un disco redondo de radio con una abertura, en la cual se pone un tubo de paredes finas y de radio . El émbolo puede introducirse perfectamente ajustado y sin fricción en el vaso e inicialmente se encuentra en el fondo del vaso. ¿A qué altura H se elevará el émbolo, si echamos en el tubo de agua?

Solución:

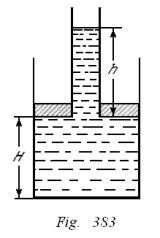
La presión sobre el fondo es igual a (fig. 383). Por otro lado, como el recipiente es cilíndrico tenemos.

La altura h podemos determinar igualando entre sí las fuerzas que actúan sobre el émbolo:, de donde resulta que

10cm.

Una pelota de goma de masa m y de radio R se sumerge en el agua a una profundidad h y luego se suelta. ¿A qué altura, a partir de la superficie del agua, saltará la pelota? Se prescinde de la resistencia del agua y del aire durante el movimiento.

Solución:

Valiéndose del principio de conservación de la energía y del principio de Arquímedes, llegamos a la siguiente ecuación:

,

Donde es la densidad del agua y , la altura que buscamos. Resolviendo la ecuación, recibimos que .

n

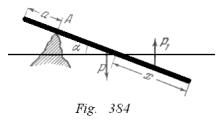
De la igualdad de los momentos respecto al punto A (fig. 384), que actúan sobre la tabla, tenemos

,

Donde ,, es el área de la sección transversal de la tabla y el peso específico del agua. De aquí resulta que

.

Como, entonces es válida solamente una solución:

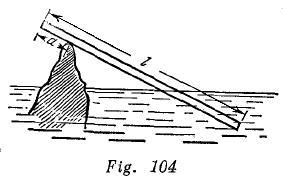
Una tabla que tiene uno de los extremos fuera del agua se apoya en una piedra que a su vez sobresale del agua. La tabla tiene la longitud . Una parte

De la tabla de longitud se encuentra sobre el punto de apoyo (fig. 104). ¿Qué parte de la tabla está hun­dida si el peso específico de madera es ?

Solución:

Not Found

The requested URL /2017/theory/191_gravitacion_universal/254.htm was not found on this server.

Apache/2.4.7 (Ubuntu) Server at fisica.ru Port 80

Un hombre que |traía una cámara de neumático, decidió facilitar su trabajo, utilizando la fuerza de empuje del aire (por la ley de Arquímedes). Para esto el hombre bombeó la cámara aumentando su volumen. ¿Obtuvo el hombre su objetivo?

Solución:

El hombre no logró su objetivo, porque, aumentando la fuerza de empuje, el hombre con ello aumentó considerablemente el peso de su carga (la densidad del aire comprimido en la cámara es mayor que la densidad del aire circundante).

En una balanza analítica de precisión que se encuentra bajo una camisa de vidrio, pesan un cuerpo. ¿Variará la indicación de la balanza, si se evacua el aire de la camisa?

Solución:

La indicación de la balanza aumentará si la densidad media del cuerpo que debe ser pesado, es menor que la densidad de las pesas de la balanza. La indicación de la balanza disminuirá, si la densidad media del cuerpo es mayor que la de las pesas de la balanza. En el caso cuando las pesas y el cuerpo tienen una densidad media igual, el equilibrio de la balanza no se alterará.

¿Cuál es el error cometido al pesar un cuerpo de volumen si al pesarlo en el aire, utilizamos pesos de cobre de masa El peso específico del cobre es y del aire es

Solución:

La verdadera masa del cuerpo es

El error relativo cometido (en %) es igual a

Calcular la masa de la atmósfera de la Tierra.

Solución:

La presión atmosférica normal es igual aproximadamente a Esto significa que el peso de una columna de aire atmosférica de área igual a es Conociendo la superficie del globo terrestre, podemos calcular la masa de toda la atmósfera de la Tierra. La superficie de la Tierra es donde es el radio medio de la Tierra. La masa de la atmósfera es toneladas.

En alta mar cayó una botella abierta. ¿Aumentará o disminuirá la capacidad de la botella bajo la presión de agua?

Solución:

Supongamos que el interior de una botella esté lleno de vidrio. Si ejercemos presión sobre la superficie exterior, entonces esta misma presión surgirá en todas las secciones interiores del vidrio. En este caso tendrá lugar una compresión, y el volumen de la parte interior de la botella disminuirá. No tiene importancia qué es lo que ejerce presión sobre la superficie interior de la botella, el agua o el vidrio que llena la botella. Si la botella se somete a una presión interna o externa, igual a P la capacidad de ésta disminuye.

Fig. 105

Un recipiente tiene la forma de un prisma (fig. 105). El fondo del recipiente es un rectángulo con dimensiones . El recipiente se llena hasta la altura con un líquido de densidad . Determinar la fuerza con que las paredes laterales actúan sobre el fondo del recipiente. El peso de las paredes se desprecia.

Solución:

La presión del líquido en el punto es nula y en el punto A es Como la presión en la pared lateral aumenta linealmente, la presión media es

La fuerza con que el líquido actúa sobre la pared lateral inclinada es

La fuerza con que las paredes laterales actúan sobre el fondo, está dirigida hacia arriba y es igual a

(La componente vertical de la fuerza resultante que actúa sobre el fondo del recipiente será igual, sin duda alguna, a la fuerza de gravedad del liquido invertido. En realidad, tenemos

donde es el volumen del líquido invertido).

Fig. 106

Un recipiente sin fondo, cuya forma y dimensiones están representadas en la fig. 106, se encuentra en una mesa. Los bordes del recipiente están bien ajustados a la superficie de la mesa. El peso del recipiente es En el recipiente se vierte un líquido. Una vez que el nivel de éste alcance una altura el recipiente bajo la acción del líquido se elevará. Determinar la densidad del líquido vertido.

Solución:

La fuerza con que el líquido hace subir el recipiente es

Por lo tanto,

Un recipiente cónico sin fondo está en una mesa. Los bordes del recipiente están bien ajustados a la superficie de la misma. Después que el nivel del líquido en el recipiente alcance una altura la presión del agua hará subir el recipiente. El radio de la base inferior del recipiente (que es mayor) es igual a , el ángulo entre la generatriz del cono y la vertical es , el peso del recipiente es . ¿Cuál es la densidad del líquido introducido?

Solución:

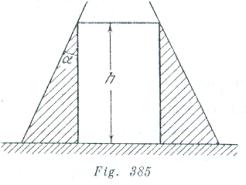
La presión sobre “el fondo” del recipiente es igual a La fuerza con que la parte sombreada del liquido (fig. 385) presiona sobre la mesa es Por la tercera ley de Newton tenemos que la misma fuerza actúa sobre el liquido. La condición de equilibrio del líquido en el momento cuando el recipiente deja de presionar sobre la mesa, tiene la forma

donde es el peso de toda la parte sombreada del líquido (el cono truncado sin el volumen del cilindro):

de donde hallamos que

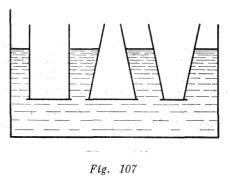
Tres recipientes con fondo falso se sumergieron en el agua a una misma profundidad. El fondo de cada uno de los recipientes (fig. 107) caerá, si vertemos en ellos de agua. ¿Caerán los fondos, si se echa en los recipientes de óleo? ¿Si los llenamos de de mercurio? ¿Si colocamos en cada recipiente un peso de ?

Solución:

En el recipiente cilíndrico el fondo caerá en todos tres casos, porque la fuerza de presión sobre el fondo del recipiente desde arriba, será la misma todas las veces. En el recipiente que se estrecha en la parte superior, el fondo caerá sólo si vertemos aceite, ya que el nivel del aceite será aquí mayor que en el recipiente cilíndrico. En el recipiente que se hace más ancho en la parte superior, el fondo caerá al poner mercurio, cuyo nivel será mayor que en el recipiente cilíndrico; lo mismo tendrá lugar si colocamos un peso que se distribuye, en el caso dado, por una superficie menor que en otros dos casos.

Dos vasos cilíndricos comunicantes están llenos de mercurio y sobre el mercurio se echa el agua. El nivel del agua en ambos vasos es igual. ¿Serán iguales los niveles de agua y de mercurio, si en uno de los vasos metemos un pedazo de madera y en el otro echamos una cantidad de agua equivalente al peso del pedazo de madera? Analizar los casos cuando los vasos tienen iguales y diferentes secciones.

Solución:

Si el nivel del agua es igual en los vasos, entonces también será igual el nivel del mercurio hasta el momento, cuando en él se introduce el pedazo de madera. La introducción en el vaso de un pedazo de madera será lo mismo que si ponemos una cantidad de agua igual a la desplazada por este pedazo, es decir, una cantidad de agua igual en peso al pedazo de madera. Por consiguiente, si las secciones de los vasos son iguales, los niveles del agua y del mercurio en ambos vasos coincidirán. Si las secciones son diferentes el agua estará por encima y el mercurio más abajo en el vaso, cuya sección es menor. Esto tiene lugar, porque la adición de cantidades iguales en peso (y en volumen) de agua en los vasos con diferentes secciones conduce a un aumento diferente de presión sobre la superficie del mercurio.

Dos vasos cilíndricos comunicantes con secciones transversales, de diferentes áreas, están llenos de mercurio. En el vaso más ancho se pone un cubo de hierro de volumen ; como consecuencia de esto, el nivel de mercurio en este vaso subió. Luego, en este mismo vaso se vierte el agua hasta el momento, en que el nivel de mercurio alcance la posición anterior. Encontrar la altura de la columna del agua si el área de la sección transversal del vaso estrecho es igual a

Solución:

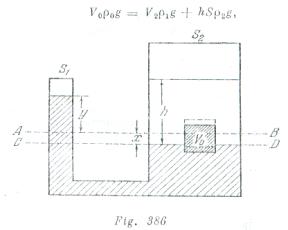
Al introducir el cubo en el segundo vaso el mercurio en ambos recipientes se elevará a una altura y ocupará la posición (fig. 386). La altura necesaria de la columna de agua en el segundo vaso se halla por la igualdad de las presiones, por ejemplo, en el nivel donde es la densidad del mercurio y la densidad del agua; y puede determinarse, valiéndose de la condición de conservación del volumen del mercurio: donde es el volumen del mercurio desplazado por el cubo después de verter el agua. Si el agua cubre completamente el cubo, entonces, por el principio de Arquímedes podemos escribir

donde es la densidad de hierro. Resolviendo las ecuaciones escritas obtenemos que

Si el agua no cubre el cubo, entonces el principio de Arquímedes se describirá de la siguiente forma:

donde es el área de una cara del cubo. En este caso, la altura que buscamos será:

La primera solución es valida sí

y la segunda sí

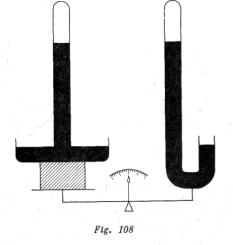
En una balanza de gran sensibilidad fueron equilibrados dos barómetros de mercurio: uno en forma de platillo (con un plato ancho) y el otro en forma de (fig. 108). Los barómetros están hechos del mismo material, tienen el mismo diámetro de los tubos y contienen la misma cantidad de mercurio. Las distancias entre las partes soldadas de los tubos y los niveles superiores del mercurio en ellos son iguales. ¿Cómo variará el equilibrio de la balanza si aumenta la presión atmosférica?

Solución:

Como resultado de la variación de la presión atmosférica, la fuerza de Arquímedes que actúa sobre los barómetros por parte del aire se varía tanto por el cambio de la densidad del aire, como por el cambio del volumen de los barómetros, cuando se cambian los niveles del mercurio en sus secciones abiertas. Tomando en consideración todas las condiciones del problema, los barómetros tienen no sólo el mismo peso, sino también el mismo volumen. Por eso, para cada uno de ellos la variación de la fuerza de empuje, debido a la primera causa, es la misma. La variación de los volúmenes, como es evidente,

Será diferente. En el barómetro en forma de U, para una variación de la diferencia de niveles en un determinado valor, el nivel del mercurio en cada caño acodado debe cambiar sólo en la mitad de este valor. En el barómetro de cubeta el nivel del mercurio en la cubeta cambia muy poco y en el tubo cambia prácticamente en todo el valor de variación de la diferencia de niveles. Además, en la misma cantidad en que cambia el volumen del mercurio dentro del tubo variará el volumen en la cubeta. Por consiguiente, para el barómetro de cubeta, la variación del volumen será dos voces mayor que para el barómetro en forma de U (a diámetros iguales de los tubos). Al aumentar la presión, el volumen del barómetro de cubeta se hace menor que el volumen del barómetro en forma de U, la fuerza de Arquímedes que actúa sobre el barómetro de cubeta también será menor y por eso él pesa más.

Un colchón de aire está lleno hasta una determinada presión que pasa la atmosférica. ¿En qué caso la presión del aire en el colchón será mayor: cuando el hombre está de pie sobre éste, o cuando está acostado?

Solución:

Cuando el hombre está en pie sobre el colchón, todo su peso se distribuye en un área menor (área de la planta de los pies), que cuando está acostado. Por eso el estado de equilibrio se alcanzará, en primer caso, para una presión mayor del aire en el colchón que en segundo caso.

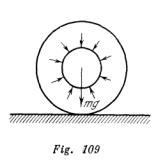
La rueda de un automóvil está construida del siguiente modo: en la llanta metálica de la rueda se pone una cámara de goma colocada dentro de una cubierta. Luego la cámara se llena de aire. La presión del aire en las partes inferior y superior de la cámara es igual. Además de la presión del aire, sobre la llanta actúa una fuerza de gravedad (fig. 109). ¿Por qué la llanta no cae? ¿Qué es lo que mantiene la llanta en estado de equilibrio?

Solución:

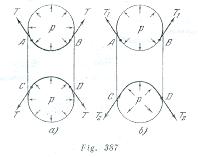
Analicemos primeramente la cámara llena de aire (en la fig. 387, vemos el corte de la cámara). Para el equilibrio de las secciones de la cámara y es evidente la necesidad de que la tensión de las paredes estiradas de la cámara equilibre la presión excesiva en el interior de la cámara. Analicemos, ahora, las fuerzas que actúan sobre las secciones y en el caso cuando la cámara está colocada en la rueda cargada (fig. 387, ). En la parte superior de la cámara la distribución de las fuerzas que actúan sobre la sección no cambia esencialmente. En la parte inferior la situación será absolutamente diferente. Sobre la sección actuará una fuerza elástica por parte de la llanta igual a la carga aplicada a la rueda (el peso de la rueda y un cuarto del peso del automóvil). Bajo la acción de esta fuerza adicional, la cámara se deforma y el ángulo entre las fuerzas de tensión de la goma aumenta. La fuerza resultante de la tensión que actúa sobre la sección disminuye y por eso la presión excesiva del aire dentro de la cámara equilibran tanto la fuerza de tensión como el peso de la rueda y una parte del automóvil.

De esta forma la llanta no cae, porque ella se mantiene por la presión excesiva del aire dentro de la cámara. En la parte superior de la cámara, esta presión excesiva se equilibra por la tensión de las paredes de ésta, y en la parte inferior, tanto la tensión disminuida de las paredes, como la fuerza aplicada a la rueda.

Una caldera de vapor está compuesta de una parte cilíndrica y de dos fondos semiesféricos (fig. 110). Los radios de la parte cilíndrica y de ambos fondos de la caldera son iguales. El grosor de la pared de la parte cilíndrica es de Todas las partes de la caldera están hechas del mismo material. ¿Cuál debe ser el grosor de las paredes de los fondos para que la resistencia de todas las partes de la caldera sea igual?

Solución:

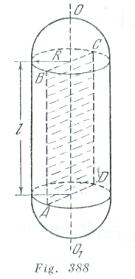
La fuerza con que se estira la pared de la parte cilíndrica de la caldera en dirección perpendicular al eje de ésta es igual por unidad de longitud a donde es el área de la sección de la caldera y , la presión en el interior de la caldera (fig. 388); es la fuerza que actúa sobre una mitad del cilindro (véase el problema 156).

El valor máximo de la fuerza por unidad de longitud de los fondos esféricos, puede hallarse de la fórmula

Por lo tanto, los fondos esféricos pueden soportar una presión dos veces mayor que la parte cilíndrica de la caldera (para el mismo espesor de las paredes). Para que la resistencia de la caldera sea igual en todas sus partes, el espesor de los fondos puede ser dos veces menor que el espesor de las paredes cilíndricas, es decir,

¿Qué forma debe tener una caldera de vapor, a fin de que la resistencia de la caldera, siendo el grosor de las paredes dado, sea máxima?

Solución:

La forma de la caldera debe ser tal que la fuerza aplicada a una unidad de longitud de la sección de la caldera sea la mínima. Esta fuerza es igual donde es el área da la sección de la caldera; , el perímetro de la sección; la presión del vapor. La fuerza será mínima, si la relación entre el área de la sección y el perímetro de la sección es mínima. Como se sabe, esta relación tiene su valor mínimo para un círculo. Además se sabe que la sección de una esfera en cualquier plano es un círculo. Por eso la forma más ventajosa de la caldera, desde el punto de vista de su resistencia, es la forma esférica.

Un recipiente con agua cae con aceleración ¿Cómo variará la presión en el vaso en función de la profundidad?

Solución:

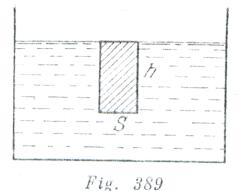
Separamos en el interior del líquido una columna de altura (fig. 389). La ecuación de movimiento de esta columna tiene la forma: donde es la masa del liquido; la presión a una profundidad Por consiguiente,

Un recipiente con un cuerpo que flota en él, cae con aceleración ¿Subirá el cuerpo a la superficie en estas condiciones?

Solución:

Conforme a la solución del problema 271, la fuerza de empuje puede escribirse en la forma siguiente: donde es el volumen de la parte sumergida del cuerpo. La ecuación de movimiento del cuerpo flotante de masa tendrá la forma: de donde recibimos que lo mismo que en un recipiente inmóvil. El cuerpo no emergerá.

Fig. 111

Una cisterna, cuya forma se da en la fig. 111, está llena hasta el máximo de agua y se mueve con aceleración en la dirección horizontal. Determinar la fuerza con que el agua actúa sobre la tapa de la cisterna.

Solución:

La presión del líquido sobre la tapa de la cisterna, a una distancia x de la parte delantera, es. Como esta presión crece linealmente a medida que nos alejamos de la pared delantera, la fuerza que buscamos será igual a

En el problema anterior determinar la fuerza con la cual el agua actúa sobre el fondo de la cisterna.

Solución:

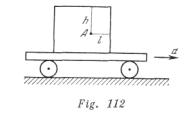
En un carrito se halla un depósito de forma cúbica, lleno de agua hasta el borde (fig. 112).El carrito se mueve con aceleración a. Determinar la presión a una profundidad h, en el punto A, alejado de la pared delantera a una distancia l, si el depósito está cerrado herméticamente con una tapa.

(Durante el movimiento uniforme la tapa no ejerce presión sobre el agua)

Solución:

Si el tanque estuviese en reposo o se moviese uniformemente, la presión a una profundidad h sería igual a Por otro lado, si el tanque tuviese un movimiento acelerado y no existiese la fuerza de gravedad, entonces la presión en el punto A sería igual a Esta es precisamente la presión que, de acuerdo con la segunda ley de Newton, hubiera trasmitido a la columna del líquido de longitud l la aceleración necesaria a. Durante el movimiento acelerado del tanque en el campo gravitacional surgirá tanto la presión , como la presión . De acuerdo con el principio de Pascal, la presión en el líquido es igual en todas las direcciones. Por eso, las presiones y se suman y la presión resultante en el punto A será igual a

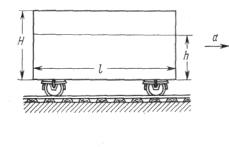
Fig. 113

Un depósito rectangular sin tapa (las dimensiones del depósito están indicadas en la fig. 113) se mueve con aceleración a. El tanque está lleno de agua hasta una altura h. ¿Cuál debe ser la aceleración a, para que el agua comience a desbordarse?

Solución:

Tenemos (fig. 390)

,

<

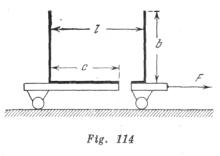
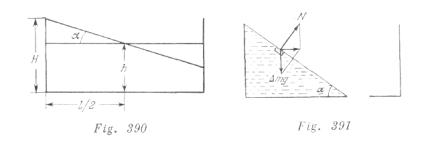
Un recipiente con agujero en el fondo se coloca en un carrito. La masa del recipiente con el carrito es M, el área de la base del recipiente es S. ¿con qué fuerza F es necesario tirar del carrito para que en el recipiente quede la máxima cantidad de agua? Las dimensiones del recipiente están indicadas en la fig. 114. Rozamiento no lo hay.

Solución:

A fin de que el líquido no se desborde, debemos transmitir al recipiente una aceleración, de modo que la superficie del líquido ocupe la posición mostrada en la fig. 391. El volumen máximo del líquido es igual a La masa de todo el sistema es La aceleración necesaria se determina por la condición de que la suma de las fuerzas que actúan sobre un pequeño volumen del líquido de masa cerca de la superficie, esté dirigida horizontalmente (fig. 391). Por la segunda ley de Newton, tenemos Por consiguiente, la fuerza que buscamos es

¿Se pude con ayuda de un sifón trasegar el agua a través de una pared de 20m de altura?

Solución:

El movimiento del líquido en el sifón está garantizado por las fuerzas de cohesión entre los elementos del líquido. El líquido en una columna larga pesa más que el líquido en la columna corta que conduce al bombeo de éste. Basándose en esta afirmación, se podrá concluir que con la ayuda del sifón es posible trasegar el agua por encima de una pared de cualquier altura. Sin embargo, esto no es así. A una altura de elevación igual a 10m, la presión dentro del líquido se hace nula. Surgirán, entonces, burbujas de aire existentes siempre en el agua, que comenzarán a dilatarse y la columna de agua dejará de ser continua. En cuanto ocurra esto, el sifón dejará de funcionar.

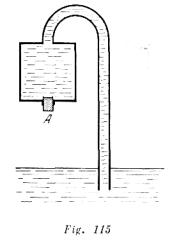
Un recipiente, mostrado en la fig. 115, está completa­mente lleno de agua. ¿Qué ocurrirá si sacamos el tapón A? El radio del agujero es 0,5 cm.

Solución:

Inicialmente el aparato funcionará como un sifón. El agua correrá por un tubo fino al recipiente de agua. Luego a través de A pasará una burbuja de aire y dividirá el líquido en la columna superior en dos partes. Después de esto el líquido dejará de correr.

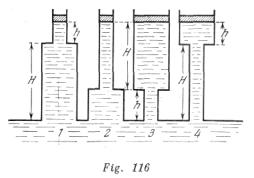
Cuatro bombas de émbolo están hechas de unos sectores de tubos de diámetros grandes y pequeños. Las bom­bas han elevado el nivel de agua a una misma altura H + h (fig. 116). ¿Por el cuál de los pistones es ne­cesario tirar con mayor fuerza para mantenerlo en equilibrio? Despreciar el peso de los pistones.

Solución:

La presión del agua inmediatamente debajo del émbolo de cada bomba será menor que la presión atmosférica en un valor de , donde es la densidad del agua. Por eso, para mantener el émbolo es necesario tirar por él hacia arriba con una fuerza, donde S es el área del émbolo. Por consiguiente, es preciso utilizar una fuerza mayor para empujar los émbolos que tienen un área mayor.

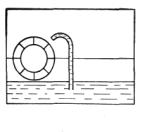
Fig.117

Se ha propuesto el siguiente proyecto del perpetuum móbile (fig. 117). Un recipiente hermético se divide en dos partes por amparo hermético, a través del cual pasa un tubo y una turbina hidráulica de cons­trucción especial. Las cámaras de la turbina tienen tapas que se abren y se cierran automáticamente.

La presión en la parte inferior del recipiente es mayor que la presión en la parte superior, y el agua sube por el tubo, llenando la cámara abierta de la turbina. Luego la cámara se cierra y la rueda gira. En la parte inferior del recipiente, la cámara se abre automáticamente devolviendo el agua. Luego, la cámara otra vez se cierra herméticamente, etc. ¿Por qué dicha construcción no funcionará eterna­mente?

Solución:

Las cámaras se llenan en la parte inferior de un aire más denso. El aire sale de las cámaras en la parte superior. Como resultado de ello, la presión se igualará paulatinamente y la máquina trabajará sólo hasta el momento cuando la diferencia de las presiones entre las partes del recipiente será suficiente para hacer subir el agua por el tubo a la parte superior del recipiente.

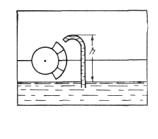
Fig. 118

Fue sugerida la siguiente variable de construcción del motor descrito en el problema 281.Las cámaras hermética (figura 118) se llenan de agua en la parte derecha de la rueda y se bajan. En el fondo las cámaras se abren y, a diferencia del proyecto anterior (problema 281) las paredes de la cámara se cierran automáticamente en el interior de la rueda. En la parte superior del recipiente, las paredes se abren automáticamente y se llenan de agua. En lo demás el perpetuum mobile esta construido del mismo modo que el descrito anteriormente, ¿Por qué este motor tampoco funcionará?

Solución:

En el caso dado, la rueda no es simétrica y la presión del aire sobre la parte derecha de la misma es mayor a la presión sobre la parte izquierda. La fuerza de la presión excesiva que actúa sobre la parte derecha de la rueda es igual a S. donde S es el área de la sección transversal de la cámara. El peso de las cámaras llenadas de agua no puede superar como, entonces . La rueda empezara a girar en sentido antihorario. Por eso las cámaras se elevaran de la parte inferior del recipiente a la parte superior llena de aire. La rueda girara en sentido antihorario hasta que la disminución de la diferencia de presiones no se haga insuficiente para elevar el agua a una altura .

¿Por qué es imprescindible durante el ascenso de un globo estratosférico llevar a bordo un lastre? Se sabe que el peso excedente en realidad reduce el “techo” del globo estratosférico.

Solución:

El “techo” del globo estratosférico no se determina por la altura máxima que puede alcanzar el globo, pero si por la altura para la cual es descenso se hace con una velocidad que garantice la “seguridad” de aterrizaje. Como se sabe la envoltura del globo estratosférico se llena de un gas ligero (hidrógeno o helio) solamente de manera parcial y como, en el proceso de ascensión del globo, este gas se dilata expulsando de la envoltura el aire, esto permite mantener la fuerza de ascensión mas o menos constante. A cierta altura el gas ocupara todo el volumen de la envoltura. Sin embargo, después de ello la fuerza ascensional de globo estratosférico aun sigue aumentándose debido al escape del gas por el orificio inferior de la envoltura. Con ello el peso del globo empieza a disminuir, solo después de que una determinada cantidad de gas se escapa de la envoltura, el globo estratosférico alcanzara el “techo”. Para el descenso del globo es preciso librar una cantidad adicional de gas a través de la válvula superior de la envoltura, para un descenso suave, la fuerza ascensional deberá ser apenas un poco menor que el peso del globo estratosférico. A una altura pequeña la velocidad de descenso resultara excesivamente grande porque el volumen del gas disminuirá y su cantidad será menor que en el proceso de la ascensión. Tirando el lastre fuera, se recibirá la disminución de la velocidad de descenso.