¿Por qué la sombra de las piernas en la tierra tiene un contorno neto, y la de la cabeza es más difusa? ¿En qué condiciones la sombra de todas las partes se vera bien?
Solución
Solamente la sombra de la fuente puntual se vera bien en todos los lugares. Las secciones aisladas de la fuente larga crean sombras que se sobrepone la una sobre la otra. En este caso, la sombra tendrá un contorno tanto más nítido, cuanto menor sea la distancia desde el objeto hasta la superficie en que se forma la sombra, por que en este caso, las distancias entre los límites de las sombras, de diferentes secciones de la fuente, serán menores. Es precisamente por eso que las piernas tienen una sombra más ostensible que la cabeza.
¿Cómo debe sostenerse un lápiz sobre la mesa con el fin de obtener una sombra bien ostensible, si la fuente luminosa es una lámpara de luz diurna en forma de tubo largo, colgada en el techo?
Solucion
El lápiz debe colocarse paralelamente a la lámpara y posiblemente más cera de la mesa. En este caso, las sombras creadas por secciones aisladas de la lámpara casi que exactamente se sobreponen las unas sobre las otras. Si el lápiz esta perpendicularmente a la lámpara, entonces las sombras de las secciones aisladas de la lámpara están tan desplazadas las unas respecto a las otras que una sombra visible no se forma.
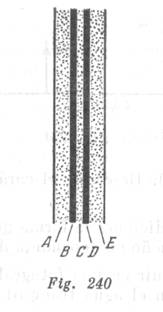
En el otoño, cuando los árboles pierden su follaje, con frecuencia se puede ver la sombra de dos ramas paralelas. La inferior proyecta una sombra oscura, bien visible y la superior una sombra mas ancha y clara.
Si ambas sombras se sobreponen casualmente, vemos una franja clara, luminosa en el medio de la sombra mas oscura, de tal modo que esta sombra parece como si fuera doble. ¿Cómo explicar este fenómeno?
Solucion
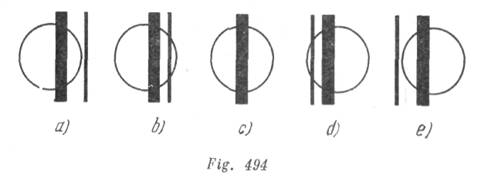
El fenómeno puede observarse en el caso cuando la distancia angular entre las ramas sea menor que el diámetro angular del disco solar. Supongamos, para mejor precisión, que la rama inferior es más gruesa que la rama superior. Para comprender por que la iluminación dentro de la sombra cambia del modo como fue indicado en la condición del problema, supongamos que estemos mirando al sol desde diferentes secciones de la sombra alternativamente.
Al lado de la sombra, el disco solar se ve por completo. Mientras que el ojo esta en la sección de la sombra A (fig 240), el se encuentra en la semisombra de la rama inferior. Delante del disco solar se ve solamente esta rama (fig 494, a).
Como esta cubre una parte del disco solar, la iluminación de este punto será menor. Moviendo el ojo hacia la posición B (fig 240), nosotros veremos que la segunda rama también cubre en parte el disco solar (fig. 494, b). Por eso la iluminación será todavía menor. En el movimiento ulterior, el ojo ocupara una posición C (fig. 240), en que ambas ramas se sobreponen la una sobre la otra (fig. 494, c). Ahora, la parte del disco solar cubierta por las ramas se hace menor y por consiguiente, la iluminación será mayor como se ve el disco solar desde las secciones D y E esta representado en la figura 494, d y e. Este hecho explica la luminosidad con que se ve la franja central de la sombra en comparación con las secciones vecinas.
Los rayos solares, pasando a través de un pequeño orificio entre el follaje de la cima de un árbol alto, proyectan en la tierra una sombra en forma de elipse. Los ejes mayor y menor del elipse son iguales a 
y 
, respectivamente. ¿Cuál es la altura 
del árbol? Las dimensiones angulares del disco solar 
.
Solucion
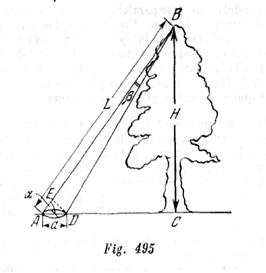
Como vemos en la fig. 495, 
sen y
, donde 
es el diámetro de la sección transversal del cono luminoso cerca de la superficie de la tierra. Siendo la dimensión angular del disco solar 
, obtenemos que 
Por consiguiente,
¿Cuál debe ser la altura mínima de un espejo plano, sujeto verticalmente en una pared, para que un hombre pueda verse su imagen sin mover la cabeza? ¿A que distancia del suelo debe encontrarse el borde inferior del espejo?
Solucion
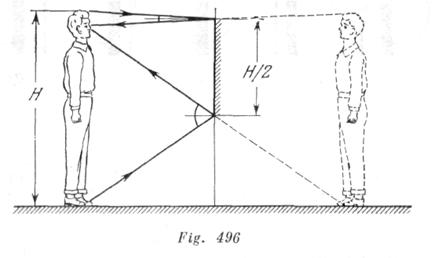
La altura del espejo debe ser igual a la mitad de la altura del hombre. La distancia desde el borde inferior del espejo hasta el suelo debe ser igual a la mitad de la distancia desde los ojos del hombre hasta las plantas de sus pies (fig. 496).
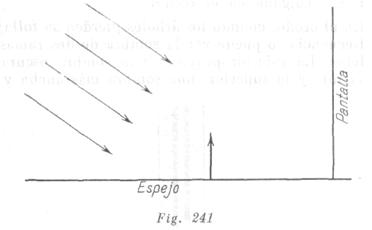
Los rayos solares, reflejándose de un espejo colocado horizontalmente, caen sobre una pantalla puesta verticalmente. En el espejo se encuentra un objeto alargado (fig. 241).
Describir el carácter de la sombra en la pantalla.
Solucion
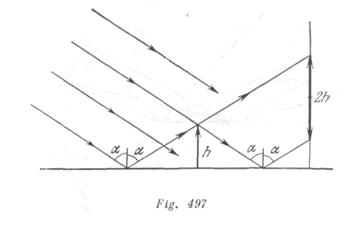
Supongamos que 
sea la altura del objeto y 
, el ángulo de incidencia de los rayos en el espejo (fig. 497). Si la pantalla se encuentra a una distancia
tg del objeto, entonces en la pantalla se verán dos sombras, una derecha y otra izquierda, unidas por sus bases. La longitud total de la sombra será 
. La sombra iluminada por el sol se destaca en contraste con las demás secciones de la pantalla, iluminadas por los rayos directos y reflejados. Si la pantalla esta puesta mas cerca, la longitud de la sombra será menor que y en ella existirán partes no iluminadas ni por los rayos directos ni por los reflejados.
Para qué condiciones la forma de la reflexión solar de un espejo pequeño no dependerá de la forma del espejo?
Solucion
Una fuente luminosa puntual siempre produce una reflexión, cuya forma se determina por la forma del espejo. El Sol tiene dimensiones finitas. Cada pequeño sector iluminado de la superficie nos da una mancha clara, que refleja la forma del espejo. Estas manchas de diferentes sectores del Sol se sobreponen los unos sobre los otros y dan un cuadro más o menos vago. Si la superficie, en la cual se observa la reflexión se encuentra lejos del espejo, entonces la forma de la mancha luminosa no dependerá de la forma del espejo. Solamente a una distancia pequeña del espejo, la mancha reflejará la forma del espejo, porque los ángulos, bajo los cuales los rayos inciden sobre el espejo de diferentes sectores del Sol, se diferencian muy poco entre sí.
Cómo distinguir en una fotografía un paisaje real de su reflexión en el agua tranquila?
Solucion
El paisaje reflejado nosotros vemos, como si estuviéramos mirando en él desde un punto situado sobre la superficie del agua a una distancia igual a la del objetivo de la cámara fotográfica hasta el agua.
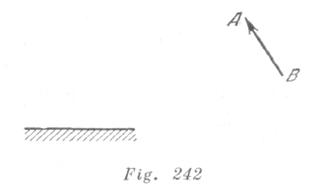
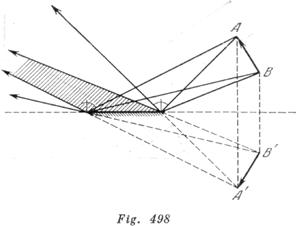
Encontrar gráficamente para qué posiciones del ojo, el observador puede ver en un espejo, de dimensiones finitas.
La imagen de un segmento de recta, situado con relación al espejo de manera, como muestra la fig. 242.
Solucion
La imagen del segmento AB se verá por completo solamente si el ojo del observador está situado dentro de la región sombreada en la fig. 498.
Un espejo plano se coloca paralelamente a una pared, a una distancia l de esta. La luz provocada por una fuente puntual, sujetada en la pared, cae sobre el espejo
y, reflejándose, forma en la pared una imagen. ¿Con qué velocidad se moverá la imagen por la pared, si aproximamos el espejo a ésta con velocidad v? ¿Cómo cambiaran las dimensiones de la imagen?
Solucion
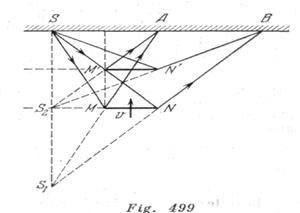
Durante el movimiento del espejo MN en dirección a la pared, la posición de la reflexión AB sobre la pared, como se ve bien en la fig. 499, permanecerá invariable (
y 
son las imágenes de la fuente S en dos posiciones del espejo:MN y
). Las dimensiones de la reflexión tampoco cambiarán, continuando todo el tiempo iguales al doble de las dimensiones del espejo.
Aprovechando las condiciones del problema 711, determinar si cambiará la iluminación de la pared en el lugar, donde se encuentra la imagen, al moverse el espejo. Considerar las dimensiones del espejo mucho menores que la distancia entre el espejo y la fuente luminosa.
Solucion
Si prescindimos de las pérdidas durante la reflexión, la iluminación de la reflexión será siempre cuatro veces menor que la iluminación del espejo. Al mismo tiempo, la iluminación del espejo varía como resultado del cambio de la distancia desde la lámpara hasta el espejo y como resultado del cambio del ángulo de incidencia de los rayos.
Para un espejo pequeño tendremos máxima iluminación a una distancia desde el espejo hasta la pared igual a 
, donde d es la distancia desde la fuente luminosa hasta el punto de la pared, a la cual se acerca el espejo (fig. 499).
Un espejo plano gira con una velocidad angular constante. El número de rotaciones por segundo es 
¿con que velocidad se desplazará una imagen por una pantalla esférica de radio igual a 10 m, si el espejo se encuentra en el centro de curvatura de la pantalla?
Solucion
Al moverse el espejo en un ángulo 
, el rayo reflejado girará en 
, porque el ángulo de incidencia aumentará en y el ángulo de reflexión aumentará en igual magnitud. Por lo tanto, la velocidad angular de rotación del rayo reflejado es 
La velocidad lineal del movimiento de la reflexión por la pantalla es 
.
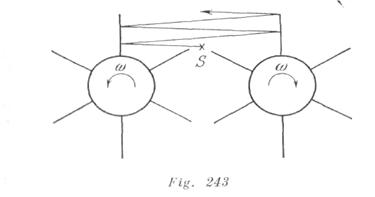
Las experiencias de A.A. Belopolski acerca de la investigación experimental del efecto óptico Doppler, consistían en la observación de la luz reflejadamente repetidamente
1) Conociendo la velocidad angular
derotación de los discos, encontrar la velocidad angular de rotación del rayo que sufre n reflexiones sucesivas de los espejos.
2) Encontrar la velocidad lineal de la enésima imagen en el momento, en que los espejos están paralelos el uno al otro y se mueven sus partes reflectores con
velocidad v en sentidos opuestos.
Solucion
1) El rayo reflejado del primer espejo forma con el rayo incidente un ángulo 
, donde 
es el ángulo de incidencia. Durante un intervalo de tiempo t , el espejo girará en un ángulo 
y el nuevo ángulo de incidencia será 
. El ángulo de reflexión también será igual a este. Por consiguiente, el ángulo entre el rayo incidente y el rayo reflejado aumentará en 
, es decir, el rayo reflejado girará en un ángulo . Gracias a ello, el ángulo de incidencia en el segundo espejo, si éste no girara, sería igual a 
, donde 
es el ángulo de incidencia, estando los discos inmóviles. Pero, durante el tiempo t, el espejo también gira en un ángulo , por eso el ángulo de incidencia se hace igual a 
. El ángulo de reflexión será también este mismo. De esta manera, después de dos reflexiones, el rayo gira en un ángulo 
con relación a su dirección, estando los espejos inmóviles. Después de tres reflexiones
el rayo gira en 
, después de n reflexiones, en 
. De este modo, la velocidad angular será 
2) La imagen en el espejo que va alejándose de la fuente con velocidad v, se alejará de la fuente con velocidad 2v y del segundo espejo, con velocidad 3v. Por eso, la segunda imagen se mueve con velocidad 3v respecto al segundo espejo y con velocidad 4v respecto a la fuente. La velocidad de la tercera imagen respecto a la fuente, será 6v y la velocidad de la enésima será 2nv.
Resolver el problema 714 para las condiciones en que los discos giran en el mismo sentido.
Solucion
1) Al moverse el primer espejo en un ángulo
, el rayo reflejado se moverá en un ángulo 
(véase la resolución del problema 714). De tal manera, aumentará en el ángulo de incidencia en el segundo espejo y, si éste no girara, el ángulo de reflexión también aumentaría en . Después de dos reflexiones, el rayo giraría en comparación con el caso de los espejos inmóviles, en un ángulo . No obstante, como consecuencia de la rotación del segundo espejo, el ángulo de incidencia del rayo en éste, durante un tiempo t, disminuirá en 
. En igual magnitud disminuirá el ángulo de reflexión, por eso el rayo reflejado tendrá la misma dirección, que en el caso de los discos inmóviles. Como tal razonamiento puede efectuarse para cualesquiera de las dos reflexiones consecutivas, la velocidad angular de rotación del rayo, que sufre n reflexiones, será:
si n es par; 
si es impar.
2) La primera imagen se aleja de la fuente con velocidad 2v y del segundo espejo con velocidad v. Por consiguiente, la segunda imagen se mueve con relación al segundo espejo con velocidad -v, o sea, ella está inmóvil respecto a la fuente. Continuando este razonamiento, encontramos que la velocidad lineal incógnita de la enésima imagen será nula, si n es par y será igual a 2v, si n es impar.
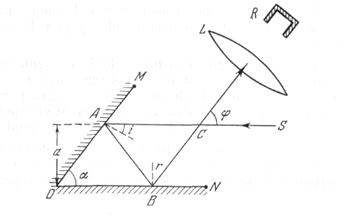
Un haz fino de luz S incide en un ángulo diedro 
formado por espejos planos iguales OM y ON, sujetados en el eje O(fig. 244). Después de reflejarse en los espejos, la luz se enfoca por una lente L y cae sobre un receptor fijo R. Los espejos giran con una velocidad angular constante.
¿Qué parte de la energía luminosa del haz, en un espacio de tiempo mucho mayor que el período de rotación, alcanzará el receptor, si el haz pasa a una distancia a
del eje, igual a la mitad de la longitud del espejo OM?
Solucion
El rayo reflejado del espejo ON forma con el rayo incidente un ángulo 
(véase la fig. 244), que no depende del ángulo de incidencia i. En efecto, como vemos del triángulo ABC, 
. Al mismo tiempo, en el triángulo OAB, 
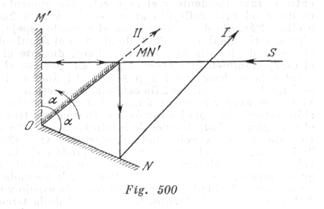
. De donde 
. Durante la rotación del espejo la dirección del rayo reflejado no cambia. Por lo tanto, si el rayo que cayó en el espejo OM, se reflejará del espejo ON, éste obligatoriamente alcanzará el receptor. Como no es difícil ver en la fig. 500, en que están mostradas las dos posiciones extremas de los espejos durante las cuales el rayo alcanza el receptor (OM, ON y 
), esto tendrá lugar en el transcurso de 1/6 de una vuelta. Por eso,1/6 parte de toda la energía del rayo alcanzará el receptor durante una vuelta y también gracias al intervalo de tiempo suficientemente grande.