Una bola pequeña y pesada fue lanzada en dirección horizontal con una velocidad inicial![]() . Hallar las aceleraciones normal y tangencial de la bola, al pasar un tiempo
. Hallar las aceleraciones normal y tangencial de la bola, al pasar un tiempo![]() desde el comienzo del movimiento.
desde el comienzo del movimiento.
Solución:
La aceleración total de la bola en cualquier punto de la trayectoria, es igual a ![]() (aceleración de caída libre). La aceleración normal es
(aceleración de caída libre). La aceleración normal es ![]() , donde
, donde ![]() es el ángulo formado por la tangente a la trayectoria con la vertical. La aceleración tangencial es
es el ángulo formado por la tangente a la trayectoria con la vertical. La aceleración tangencial es ![]() . De las consideraciones geométricas elementales, se puede obtener:
. De las consideraciones geométricas elementales, se puede obtener:
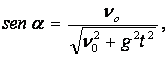
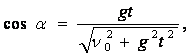
Por lo tanto
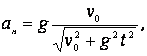
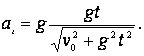
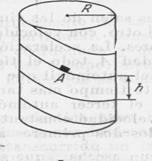
Determinar la magnitud de la aceleración del cuerpo ![]() que se desliza sin velocidad inicial por el canal helicoidal con paso
que se desliza sin velocidad inicial por el canal helicoidal con paso![]() y el radio
y el radio ![]() al final de la enésima vuelta (fig. 11). Menospreciar el rozamiento.
al final de la enésima vuelta (fig. 11). Menospreciar el rozamiento.
Solución:
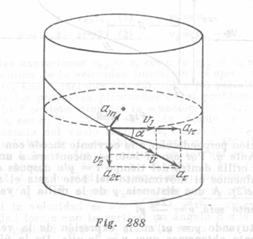
El movimiento del cuerpo puede ser analizado como la superposición del movimiento por la circunferencia de radio ![]() en un plano horizontal y de la caída por la vertical. Así la velocidad
en un plano horizontal y de la caída por la vertical. Así la velocidad ![]() del cuerpo, en un momento dado, puede ser considerada como una suma geométrica de dos componentes:
del cuerpo, en un momento dado, puede ser considerada como una suma geométrica de dos componentes: ![]() , que está dirigida horizontalmente, y
, que está dirigida horizontalmente, y ![]() que está dirigida verticalmente (fig. 288). El ángulo
que está dirigida verticalmente (fig. 288). El ángulo![]() es el ángulo formado por la línea helicoidal del canal con la horizontal.
es el ángulo formado por la línea helicoidal del canal con la horizontal.
La aceleración del cuerpo en el movimiento curvilíneo es igual a la suma geométrica de las aceleraciones tangencial y normal. La aceleración normal que corresponde al movimiento por la circunferencia es ![]() . El movimiento
. El movimiento
por la vertical es rectilíneo por eso ![]()
La aceleración incógnita es ![]() donde
donde ![]() y
y ![]() son las aceleraciones tangenciales correspondientes al movimiento circular y a lo largo de la vertical. La aceleración tangencial total, evidentemente, es igual a
son las aceleraciones tangenciales correspondientes al movimiento circular y a lo largo de la vertical. La aceleración tangencial total, evidentemente, es igual a![]() Podemos encontrarla si desenvolvemos mentalmente en el plano la superficie del cilindro, en la cual está atornillado el canal helicoidal. En este proceso el canal se transforma en un plano inclinado de altura nh y de longitud de la base
Podemos encontrarla si desenvolvemos mentalmente en el plano la superficie del cilindro, en la cual está atornillado el canal helicoidal. En este proceso el canal se transforma en un plano inclinado de altura nh y de longitud de la base![]() . Está claro que Para la determinación de
. Está claro que Para la determinación de ![]() para la determinación de
para la determinación de ![]() encontramos b partiendo del principio de conservación de la energía
encontramos b partiendo del principio de conservación de la energía ![]() . Por lo tanto,
. Por lo tanto,![]() Sustituyendo las aceleraciones encontramos
Sustituyendo las aceleraciones encontramos ![]() en la expresión para la aceleración incógnita, recibimos:
en la expresión para la aceleración incógnita, recibimos:
![]()
La velocidad de la corriente del río crece proporcionalmente a la distancia desde la orilla, alcanzando su valor máximo ![]() en el centro del río. Junto a las orillas la velocidad de la corriente es igual a cero. Un bote flota por el río de modo que su velocidad
en el centro del río. Junto a las orillas la velocidad de la corriente es igual a cero. Un bote flota por el río de modo que su velocidad ![]() con relación al agua es constante y perpendicular a la corriente. Hallar la distancia, a la cual será llevado el bote por la corriente durante el paso si la anchura del río es
con relación al agua es constante y perpendicular a la corriente. Hallar la distancia, a la cual será llevado el bote por la corriente durante el paso si la anchura del río es ![]() . Determinar también la trayectoria del bote.
. Determinar también la trayectoria del bote.
Solución:
Tomemos como origen de referencia del sistema de coordenadas el punto a, punto de partida del bote. La dirección de los ejes esta indicada en la (fig.289) el movimiento del bote en:

Dirección perpendicular a la corriente sucede con una velocidad constante ![]() . Por eso el bote se encontrará a una distancia
. Por eso el bote se encontrará a una distancia ![]() de la orilla dentro del tiempo
de la orilla dentro del tiempo ![]() después de la partida. Examinemos el movimiento del bote hasta el medio del río
después de la partida. Examinemos el movimiento del bote hasta el medio del río![]()
. A una distancia ![]() de la orilla la velocidad de la corriente será
de la orilla la velocidad de la corriente será ![]() Sustituyendo
Sustituyendo ![]() en la expresión de la velocidad de la corriente obtenemos que:
en la expresión de la velocidad de la corriente obtenemos que: ![]() .De la última relación se deduce que el movimiento del bote en dirección paralela a las orillas será realizado con aceleración constante
.De la última relación se deduce que el movimiento del bote en dirección paralela a las orillas será realizado con aceleración constante ![]() . El bote alcanzará el medio del río durante el tiempo
. El bote alcanzará el medio del río durante el tiempo![]()
.En este mismo intervalo de tiempo, el bote será llevado aguas abajo a una distancia ![]() Al moverse desde el medio del río (punto D) basta la orilla opuesta el bote será llevado por la corriente a una distancia adicional
Al moverse desde el medio del río (punto D) basta la orilla opuesta el bote será llevado por la corriente a una distancia adicional![]() . De tal modo, la distancia buscada será igual a
. De tal modo, la distancia buscada será igual a ![]() Durante el movimiento del bote hasta el medio del río, tenemos:
Durante el movimiento del bote hasta el medio del río, tenemos:
De estas relaciones determinamos ![]() . La trayectoria del bote desde el punto
. La trayectoria del bote desde el punto ![]() hasta
hasta ![]() :
: ![]() (parábola). La segunda mitad de la trayectoria
(parábola). La segunda mitad de la trayectoria ![]() tendrá el mismo carácter que la primera.
tendrá el mismo carácter que la primera.
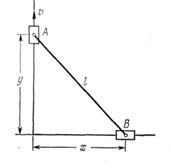
Dos carriles están unidos formando entre sí un ángulo recto. Por ellos se mueven dos carritos unidos mediante una barra articulada de longitud ![]() . El carrito
. El carrito ![]() (fig. 12) comienza a moverse del punto de intersección de los carriles y sube uniformemente con una velocidad
(fig. 12) comienza a moverse del punto de intersección de los carriles y sube uniformemente con una velocidad![]() . Determinar la ley del movimiento y la velocidad del carrito
. Determinar la ley del movimiento y la velocidad del carrito ![]() .
.
Solución:
La ley de movimiento del carrito ![]() es
es ![]() , La ley de movimiento del carrito es el movimiento del carrito B a lo largo del carro horizontal
, La ley de movimiento del carrito es el movimiento del carrito B a lo largo del carro horizontal![]() puede ser representado como la suma de dos movimientos independientes: un movimiento verticalmente hacia arriba con velocidad
puede ser representado como la suma de dos movimientos independientes: un movimiento verticalmente hacia arriba con velocidad![]() y un movimiento de rotación alrededor del punto
y un movimiento de rotación alrededor del punto![]() , con cierta velocidad
, con cierta velocidad![]() Mediante las consideraciones geométricas elementales deducimos que
Mediante las consideraciones geométricas elementales deducimos que ![]() donde
donde
![]() es la distancia del carrito
es la distancia del carrito ![]() hasta el origen de las coordenadas. De ahí obtenemos
hasta el origen de las coordenadas. De ahí obtenemos ![]()
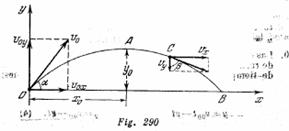
Un cuerpo fue lanzado con velocidad inicial ![]() , bajo un ángulo
, bajo un ángulo ![]() con la horizontal. ¿Cuánto tiempo dura este vuelo? ¿A qué distancia del lugar de lanzamiento caerá el cuerpo? ¿Con qué valor del ángulo a la distancia del vuelo será la máxima?
con la horizontal. ¿Cuánto tiempo dura este vuelo? ¿A qué distancia del lugar de lanzamiento caerá el cuerpo? ¿Con qué valor del ángulo a la distancia del vuelo será la máxima?
¿A qué altura estará el cuerpo dentro de un intervalo de tiempo![]() desde el comienzo del movimiento? ¿Cuáles serán la magnitud y el sentido de la velocidad del cuerpo en este momento? Considerar que
desde el comienzo del movimiento? ¿Cuáles serán la magnitud y el sentido de la velocidad del cuerpo en este momento? Considerar que ![]() es mayor que el tiempo de la elevación del cuerpo hasta la altura máxima. Menospreciar la resistencia del aire.
es mayor que el tiempo de la elevación del cuerpo hasta la altura máxima. Menospreciar la resistencia del aire.
Solución:
Las coordenadas y las velocidades del cuerpo respecto al sistema de referencia representado en la (fig. 290), en cualquier momento de tiempo se determinan por las siguientes expresiones:

En estas expresiones ![]() son las proyecciones de la velocidad inicial en los ejes
son las proyecciones de la velocidad inicial en los ejes ![]() , respectivamente. Las ecuaciones (1), (2), (3) y (4) permiten responder a todas las preguntas planteadas en el problema. El tiempo
, respectivamente. Las ecuaciones (1), (2), (3) y (4) permiten responder a todas las preguntas planteadas en el problema. El tiempo
de vuelo ![]() se determina por la ecuación (2). Para
se determina por la ecuación (2). Para![]() , tenemos
, tenemos ![]() , de donde
, de donde ![]() . La distancia del vuelo es
. La distancia del vuelo es ![]() . El valor máximo de
. El valor máximo de ![]() se obtiene para
se obtiene para![]() . En este caso tenemos
. En este caso tenemos![]() . La altura, en la cual se encontrará el cuerpo, pasado un tiempo
. La altura, en la cual se encontrará el cuerpo, pasado un tiempo ![]() , es igual a
, es igual a ![]() . La velocidad del cuerpo en el momento de tiempo
. La velocidad del cuerpo en el momento de tiempo ![]() es
es ![]() , donde
, donde ![]()
De ahí la velocidad es ![]() Esta velocidad forma con la vertical un ángulo
Esta velocidad forma con la vertical un ángulo ![]() que se determina por la igualdad
que se determina por la igualdad ![]()
Determinar la trayectoria del movimiento del cuerpo lanzado bajo un ángulo respecto a la horizontal (véase el problema 40).
Solución:
Las coordenadas del cuerpo![]() cambian con el tiempo según la ley:
cambian con el tiempo según la ley:
![]()
Excluyendo de estas expresiones el tiempo, recibimos la siguiente ecuación:
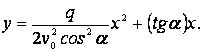
Esta es la ecuación de una parábola. Designando por![]() las coordenadas del vértice de la parábola (punto en la
las coordenadas del vértice de la parábola (punto en la ![]() (fig.290), podemos escribir la ecuación de la trayectoria de la siguiente forma:
(fig.290), podemos escribir la ecuación de la trayectoria de la siguiente forma: ![]() donde:
donde:
Es necesario lanzar desde el suelo una pelota a través de una pared vertical de altura H que se encuentra a una distancia S (fig. 13). ¿Para qué velocidad inicial mínima esto se realizará? ¿Bajo qué ángulo ![]() con relación a la horizontal deberá estar dirigida en este caso la velocidad?
con relación a la horizontal deberá estar dirigida en este caso la velocidad?
Solución:
La trayectoria de la pelota pasa por el punto con coordenadas ![]() Por lo tanto (véase el problema 41):
Por lo tanto (véase el problema 41):![]()
De esta expresión recibimos:
![]()
![]() ,
,
donde![]() . El valor mínimo de
. El valor mínimo de ![]() se obtiene para
se obtiene para ![]() y es:
y es:
![]()
La prueba de la espoleta de una granada de fragmentación se realiza en el centro del fondo de un pozo cilíndrico de profundidad H. Los fragmentos que se forman durante la explosión y cuyas velocidades no sobrepasan vq no deben caer en la superficie de la tierra. ¿Cuál debe ser el diámetro mínimo D del pozo?
Solución:
![]()
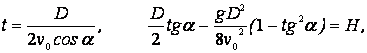
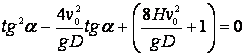
Conociendo ![]() , de la ultima ecuación recibimos dos valores para
, de la ultima ecuación recibimos dos valores para ![]() que corresponde a la trayectoria curva y recta, o dos valores iguales (en caso crítico), o ninguno (fragmento de granada no alcanza el borde del pozo). De este modo el pozo debe ser tal que esta ecuación no tenga soluciones:
que corresponde a la trayectoria curva y recta, o dos valores iguales (en caso crítico), o ninguno (fragmento de granada no alcanza el borde del pozo). De este modo el pozo debe ser tal que esta ecuación no tenga soluciones:
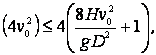
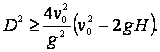
De estas expresiones se deduce que si![]() entonces
entonces ![]() puede tener cualquier valor; si
puede tener cualquier valor; si ![]() entonces.
entonces.

Un cuerpo fue lanzado al agua desde un despeñadero abrupto de altura H. La velocidad inicial del cuerpo v0 forma un ángulo ![]() con la horizontal. ¿A qué distancia de la orilla caerá el cuerpo? ¿Dentro de qué tiempo después de comenzar el movimiento, el cuerpo estará a una altura h sobre el agua? ¿Qué velocidad tendrá el cuerpo en el momento de su caída al agua?
con la horizontal. ¿A qué distancia de la orilla caerá el cuerpo? ¿Dentro de qué tiempo después de comenzar el movimiento, el cuerpo estará a una altura h sobre el agua? ¿Qué velocidad tendrá el cuerpo en el momento de su caída al agua?
Solución:
Las coordenadas y las velocidades del cuerpo en cualquier momento de tiempo respecto al sistema de referencia, representado en la (fig.292), se determina por las mismas ecuaciones que en el problema 41. En el momento de caída del agua la coordenada del cuerpo es ![]() .Por eso el tiempo de vuelo
.Por eso el tiempo de vuelo ![]() se determina por la ecuación:
se determina por la ecuación:
![]()
De esta expresión recibimos que
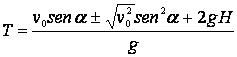
Puesto que ![]() , es preciso tomar el signo positivo. La distancia hasta la orilla es
, es preciso tomar el signo positivo. La distancia hasta la orilla es
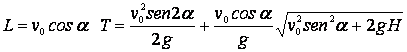
El tiempo necesario para que el cuerpo alcance una altura ![]() sobre el agua es:
sobre el agua es:
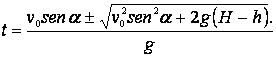
Si![]() , entonces existe sentido físico solamente para el signo positivo. Para
, entonces existe sentido físico solamente para el signo positivo. Para
![]() , existe sentido físico para ambas soluciones. El cuerpo, durante su caída, estará dos veces a la misma altura sobre el agua.
, existe sentido físico para ambas soluciones. El cuerpo, durante su caída, estará dos veces a la misma altura sobre el agua.
La velocidad final ![]() puede ser encontrada con mas facilidad mediante el principio de conservación se la energía.
puede ser encontrada con mas facilidad mediante el principio de conservación se la energía.
![]()
De esta ecuación se deduce que
![]()
¿Bajo qué ángulo respecto a la horizontal es necesario lanzar una piedra desde el despeñadero abrupto del río para que ésta caiga al agua a una distancia máxima de la orilla? La altura del despeñadero es ![]() y la velocidad inicial de la piedra es
y la velocidad inicial de la piedra es![]() .
.
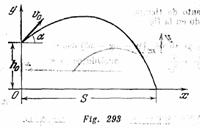
Solución:
En el sistema de referencia, representado en la (fig. 293), las coordenadas de la piedra en cualquier momento de tiempo se determinan por las siguientes ecuaciones:
![]()
En el momento de caída de la piedra![]() , donde
, donde ![]() es la distancia de vuelo de la piedra. Resolviendo estas ecuaciones con relación al ángulo
es la distancia de vuelo de la piedra. Resolviendo estas ecuaciones con relación al ángulo ![]() , decimos que
, decimos que
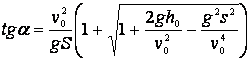
Esta expresión tiene sentido solamente para
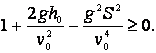
De ahí obtenemos que ![]() , de esta manera
, de esta manera ![]() . Para valores menores de
. Para valores menores de![]() a cada valor de
a cada valor de ![]() le corresponde dos valores del ángulo
le corresponde dos valores del ángulo![]() , cuya diferencia es tanto menor cuanto mas próximo sean los valores de
, cuya diferencia es tanto menor cuanto mas próximo sean los valores de ![]() al máximo. Por lo tanto, para la distancia máxima de vuelo:
al máximo. Por lo tanto, para la distancia máxima de vuelo:
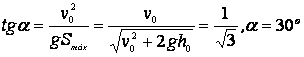
¿Con qué velocidad mínima deberá ser lanzado un cuerpo desde la cumbre de una torre de altura h para que éste caiga a una distancia S del pie de la torre?
Solución:
El movimiento del cuerpo se describe por las ecuaciones;
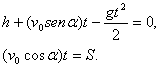
De donde recibimos:
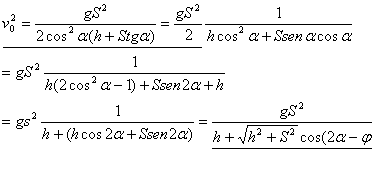
donde ![]() es un ángulo cualquiera. Por consiguiente, tenemos:
es un ángulo cualquiera. Por consiguiente, tenemos:
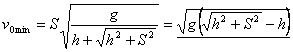
Un objeto lanzado bajo un ángulo α respecto al horizonte se está observando por un anteojo colocado en el punto de lanzamiento. ¿Para qué ángulos α habrán momentos durante el movimiento del cuerpo cuando su velocidad será perpendicular al eje del anteojo?
Solución:
En cualquier momento de tiempo, el anteojo forma con la horizontal tal ángulo ![]() , que
, que ![]() donde
donde
![]()
![]()
(son las coordenadas del objeto). El vector de velocidad del objeto forma con la horizontal un ángulo ![]() además
además ![]() Por la condición del problema:
Por la condición del problema: ![]() utilizando la formula
utilizando la formula![]() recibimos la ecuación
recibimos la ecuación ![]() Resolviendo esta ecuación tenemos
Resolviendo esta ecuación tenemos
![]()
Esta expresión tiene sentido solamente para ![]() (se obtienen dos diferentes o iguales valores reales de
(se obtienen dos diferentes o iguales valores reales de ![]()
Un bombardero en picado tira una bomba desde la altura ![]() , estando a una distancia
, estando a una distancia ![]() del objetivo. La velocidad del bombardero es
del objetivo. La velocidad del bombardero es![]() . ¿Bajo qué ángulo respecto a la horizontal debe picar el bombardero?
. ¿Bajo qué ángulo respecto a la horizontal debe picar el bombardero?
Solución:
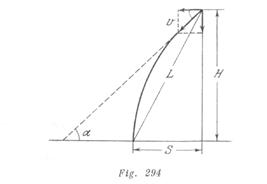
El trayecto ![]() , recorrido por la bomba en dirección horizontal, es
, recorrido por la bomba en dirección horizontal, es ![]() , donde
, donde ![]() es el tiempo de caída de la bomba. El trayecto recorrido por la vertical es
es el tiempo de caída de la bomba. El trayecto recorrido por la vertical es ![]() (fig. 294). Excluyendo el tiempo de estas ecuaciones, obtenemos
(fig. 294). Excluyendo el tiempo de estas ecuaciones, obtenemos
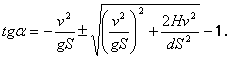
La solución tiene sentido físico sólo teniendo el signo positivo. El signo negativo corresponde a![]() , o sea el caso en que la bomba se tira cuando el avión vuela hacia arriba.
, o sea el caso en que la bomba se tira cuando el avión vuela hacia arriba.
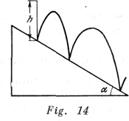
Una bola cae libremente desde la altura ![]() sobre un plano inclinado que forma un ángulo
sobre un plano inclinado que forma un ángulo ![]() con la horizontal (fig. 14). Encontrar la relación de las distancias entre los puntos, en los cuales la bola saltando toca el plano inclinado. Los choques de la bola con el plano se consideran absolutamente elásticos.
con la horizontal (fig. 14). Encontrar la relación de las distancias entre los puntos, en los cuales la bola saltando toca el plano inclinado. Los choques de la bola con el plano se consideran absolutamente elásticos.
Solución:
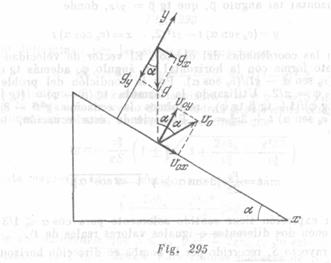
La solución del problema se simplificará sensiblemente, si los ejes de las coordenadas están dirigidos a lo largo del plano inclinado y perpendicularmente a él. (fig. 295). En este caso, las proyecciones de la aceleración de la bola en los ejes ![]()
![]()
![]() serán iguales a
serán iguales a ![]() y
y ![]() respectivamente. La velocidad de la bola en el momento del primer choque con el plano inclinado será
respectivamente. La velocidad de la bola en el momento del primer choque con el plano inclinado será ![]() La velocidad inicial de la bola, después del primer choque
La velocidad inicial de la bola, después del primer choque![]() , es y forma con el eje
, es y forma con el eje![]() un ángulo
un ángulo ![]() (fig. 295). La distancia entre los puntos del primero y segundo choques con el plano inclinado es
(fig. 295). La distancia entre los puntos del primero y segundo choques con el plano inclinado es
![]()
donde ![]() es el tiempo de vuelo. Este tiempo se determina por la ecuación
es el tiempo de vuelo. Este tiempo se determina por la ecuación
![]()
Resolviendo esta ecuación, obtenemos que ![]() y
y ![]() La velocidad de la bola en el momento del segundo choque se determina por las igualdades:
La velocidad de la bola en el momento del segundo choque se determina por las igualdades:
![]()
Terminados los choques, estas velocidades serán
![]()
La distancia entre los puntos del segundo y tercer choques es igual a
![]()
donde ![]() es el tiempo de vuelo. Puesto que la velocidad inicial a lo largo del eje
es el tiempo de vuelo. Puesto que la velocidad inicial a lo largo del eje![]() es la misma que durante el primer choque, entonces t2=t1; y, por consiguiente
es la misma que durante el primer choque, entonces t2=t1; y, por consiguiente![]() ,
,
De modo análogo puede demostrarse que la distancia entre los puntos siguientes es ![]() De este modo, recibimos la relación:
De este modo, recibimos la relación: ![]()
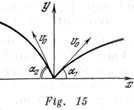
Del punto ![]() (fig. 15) se tiran simultáneamente dos objetos con la misma velocidad inicial
(fig. 15) se tiran simultáneamente dos objetos con la misma velocidad inicial ![]() bajo diferentes ángulos
bajo diferentes ángulos ![]() y
y ![]() respecto a la horizontal. ¿Cuál será la velocidad del movimiento de los objetos el uno respecto al otro? ¿Cuál será la distancia entre los objetos al pasar un tiempo
respecto a la horizontal. ¿Cuál será la velocidad del movimiento de los objetos el uno respecto al otro? ¿Cuál será la distancia entre los objetos al pasar un tiempo ![]() ? (El movimiento de los objetos es de avance).
? (El movimiento de los objetos es de avance).
Solución:
Las componentes de las velocidades de los cuerpos a lo largo de los ejes ![]() e
e ![]() se determinan, en cualquier momento de tiempo, de la siguiente manera:
se determinan, en cualquier momento de tiempo, de la siguiente manera:
![]()
![]()
![]()
![]()
Sea ![]() la velocidad del primer cuerpo con relación al segundo. Entonces
la velocidad del primer cuerpo con relación al segundo. Entonces
![]()
De modo este, la velocidad es ![]() igual a
igual a
![]()
Los cuerpos se mueven el uno respecto al otro con velocidad constante. Pasado un intervalo de tiempo ![]() , la distancia entre ellos será
, la distancia entre ellos será
![]()
De una torre fueron tirados piedras en todas las direcciones posibles con velocidad inicial ![]() Resultó que la piedra que alcanzó la tierra por una trayectoria más suave, tenía en el momento de la caída un vector de velocidad que formaba un ángulo
Resultó que la piedra que alcanzó la tierra por una trayectoria más suave, tenía en el momento de la caída un vector de velocidad que formaba un ángulo ![]() con la horizontal. Determinar la altura de la torre.
con la horizontal. Determinar la altura de la torre.
Solución:
La velocidad de cualquier piedra, en un lanzamiento dirigido a la tierra es igual a ![]() Una piedra que vuela por una trayectoria más suave, posee la mayor velocidad horizontal que es igual a
Una piedra que vuela por una trayectoria más suave, posee la mayor velocidad horizontal que es igual a ![]() . Por lo tanto,
. Por lo tanto,
![]() , de donde
, de donde ![]() .
.
Una bola elástica se tira desde una mesa de altura h, transmitiéndole cierta velocidad horizontal. En el momento cuando la bola experimentaba uno de los infinitos choques elásticos con el suelo, de la misma mesa fue lanzada horizontalmente otra bola con tal velocidad, que ésta choque con la primera. ¿A qué altura chocaron?
Solución:
La primera bola salta del suelo, teniendo la componente vertical de la velocidad ![]() . Su coordenada vertical es
. Su coordenada vertical es ![]() , mientras que la coordenada vertical de la segunda bola es
, mientras que la coordenada vertical de la segunda bola es![]() . En el momento de encuentro y1=y2, de donde concluimos que las bolas se encontraran a una altura de 0.75h.
. En el momento de encuentro y1=y2, de donde concluimos que las bolas se encontraran a una altura de 0.75h.
Un proyectil se lanza de un cañón con velocidad inicial ![]() .Determinar la «zona de seguridad», es decir, el lugar geométrico de todos los puntos del espacio, donde el proyectil no podrá caer.
.Determinar la «zona de seguridad», es decir, el lugar geométrico de todos los puntos del espacio, donde el proyectil no podrá caer.
Solución:
Según las solución del problema 43 deducimos que el proyectil no alcanzará el punto situado a una altura y, si la distancia horizontal de este punto hasta el cañón no satisface la desigualdad
![]() .
.
Así, el límite de la llamada «zona peligrosa» se determina por la ecuación
![]()
La sección de tal superficie (paraboloide) tiene la forma de una
parábola que coincide con la trayectoria del proyectil, lanzado
horizontalmente con velocidad ![]() del cañón, situado a una
del cañón, situado a una
altura ![]() .
.
La oruga de un tractor está compuesta de n eslabones. La longitud de cada eslabón es igual a a. Los radios de las ruedas, en las cuales se colocan las orugas, son R. El tractor se mueve con la velocidad v. Se supone que la oruga no se comba.
1) ¿Cuántos eslabones de la oruga se mueven en un momento dado, de un modo progresivo, cuántos reposan (respecto a la tierra) y cuántos eslabones toman
parte en el movimiento giratorio?
2) El tractor recorrió un trayecto S >> na. ¿Cuánto tiempo cada eslabón de la oruga se movía progresiva mente, cuánto tiempo reposaba y cuánto tiempo participaba en el movimiento giratorio?
Solución:
1) Designemos por L = na la longitud de la oruga. Entonces ![]() es la distancia entre los ejes de las ruedas.
es la distancia entre los ejes de las ruedas.
En el movimiento de translación participan ![]() eslabones. El igual número de eslabones se encuentra en reposo con relación a la tierra. En el movimiento giratorio toman parte
eslabones. El igual número de eslabones se encuentra en reposo con relación a la tierra. En el movimiento giratorio toman parte ![]() eslabones.
eslabones.
2) El tiempo de movimiento del tractor es ![]() . En una rotación completa de la oruga, un eslabón recorre el trayecto 2l, moviéndose de avance con velocidad igual a 2v. El tiempo del movimiento de avance del eslabón en una rotación es
. En una rotación completa de la oruga, un eslabón recorre el trayecto 2l, moviéndose de avance con velocidad igual a 2v. El tiempo del movimiento de avance del eslabón en una rotación es ![]() . En total la oruga da
. En total la oruga da ![]() vueltas. De este modo, el tiempo para el movimiento de avance de un eslabón es
vueltas. De este modo, el tiempo para el movimiento de avance de un eslabón es![]() . El eslabón permanece en reposo el mismo tiempo y participará en el movimiento giratorio durante el tiempo
. El eslabón permanece en reposo el mismo tiempo y participará en el movimiento giratorio durante el tiempo
![]() .
.
Para que vire un tractor que se mueve con una velocidad ![]() , el tractorista frena una de las orugas de modo que el eje de la rueda motriz comienza a avanzar con velocidad
, el tractorista frena una de las orugas de modo que el eje de la rueda motriz comienza a avanzar con velocidad ![]() . La distancia entre las orugas es
. La distancia entre las orugas es ![]() ¿De qué radio será la vuelta que da el centro del tractor?
¿De qué radio será la vuelta que da el centro del tractor?
Solución:
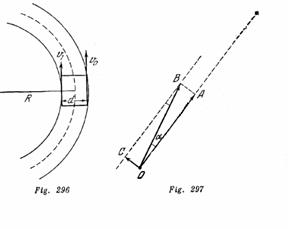
Designemos por R el radio que buscamos y por ω la velocidad angular del movimiento del tractor por el arco. Entonces resulta que![]() ,
,![]() . (Fig. 296)
. (Fig. 296)
De estas ecuaciones recibimos que
![]() ,
, ![]()
En las montañas puede observarse el siguiente fenómeno: una estrella desaparece rápidamente «a simple vista» tras una cumbre alejada. (Naturalmente, el mismo fenómeno puede observarse también en una planicie si hay una construcción bastante alta y bien alejada.) ¿Con qué velocidad es preciso correr para ver la estrella durante todo el tiempo a una misma distancia angular de la montaña? La distancia entre el observador y la cumbre de la montaña es de 10 km. La observación se realiza en el polo.
Solución:
Inicialmente el observador se encuentra en el polo (punto, fig. 297). El eje de la Tierra pasa por el punto O perpendicularmente al diseño. OA (es paralelo a BC) está dirigido a la estrella. La montaña se encuentra a la derecha del punto A. ![]() es el ángulo en el cual gira el globo terrestre durante el tiempo
es el ángulo en el cual gira el globo terrestre durante el tiempo![]() , ω es la velocidad angular de rotación de la Tierra.
, ω es la velocidad angular de rotación de la Tierra.
Para ver la estrella el observador debe recorrer, en este intervalo de tiempo, una distancia igual a ![]() . La velocidad del observador es
. La velocidad del observador es ![]() .
.
Un disco continuo rueda sin deslizamiento por el sector horizontal del camino con una velocidad constante v (fig. 16).
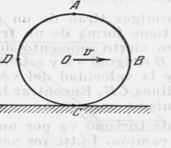
Fig. 16
1) Demostrar que la velocidad lineal de rotación respecto al centro O de cualquier punto del disco que se encuentra en su diámetro exterior es igual a la
velocidad del movimiento de traslación del disco.
2) Determinar el valor y el sentido de la velocidad de los puntos A, B, C y D situados en el diámetro exterior del disco respecto a un observador fijo.
3) ¿Qué puntos del disco tienen respecto a un observador fijo la misma velocidad, por su valor absoluto, que el centro del disco?
Solución:
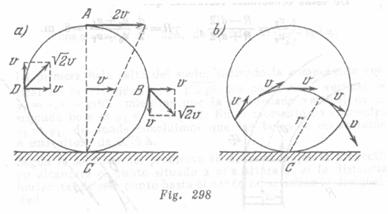
1) En el intervalo de tiempo de una rotación completa T, el disco recorrerá un trayecto igual a la longitud de la circunferencia del disco, es decir,![]() , donde r es el radio del disco. De esta manera, la velocidad de avance de cualquier punto del disco es
, donde r es el radio del disco. De esta manera, la velocidad de avance de cualquier punto del disco es ![]() . Por otro lado, la velocidad lineal de rotación con relación al centro O de los puntos que se encuentran en el diámetro exterior del disco, es igual a
. Por otro lado, la velocidad lineal de rotación con relación al centro O de los puntos que se encuentran en el diámetro exterior del disco, es igual a![]() , donde ω es la velocidad angular de rotación. En estas condiciones tenemos
, donde ω es la velocidad angular de rotación. En estas condiciones tenemos ![]() , entonces
, entonces ![]() , lo que se tenía que demostrar.
, lo que se tenía que demostrar.
2) La velocidad de los puntos del diámetro exterior con relación a un observador inmóvil, está compuesta de dos velocidades: el movimiento de avance y giratorio. Para el punto A la velocidad resultante será 2v. Para los puntos B y D las velocidades son iguales en valor absoluto, y su suma es igual a ![]() (fig. 298, a). Para el punto C la velocidad resultante con relación a un observador inmóvil, es igual a cero, ya que las velocidades de los movimientos de avance y giratorio son iguales en valor absoluto y están dirigidas en sentidos opuestos.
(fig. 298, a). Para el punto C la velocidad resultante con relación a un observador inmóvil, es igual a cero, ya que las velocidades de los movimientos de avance y giratorio son iguales en valor absoluto y están dirigidas en sentidos opuestos.
3) Las velocidades instantáneas de los puntos del diámetro AC crecen directamente proporcional a la distancia del punto C. Por eso, el movimiento del disco, en un determinado momento de tiempo, puede ser analizado como el movimiento giratorio
alrededor de su punto de contacto con el plano. El eje que pasa por el punto C, perpendicularmente al plano del disco, se denomina eje instantáneo de rotación. Este eje se desplaza durante el movimiento del disco, pasando todo el tiempo por
el punto de contacto del disco con el plano. Por lo tanto, en un determinado momento de tiempo, todos los puntos del disco que están equidistantes del punto C, tendrán la misma velocidad resultante con relación al observador inmóvil. Los
puntos, situados a una distancia del eje instantáneo (del punto C) igual al radio del disco, tendrán la misma velocidad en valor absoluto que la velocidad del eje, o sea, v (fig. 298, b).
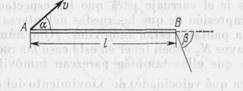
fig. 17
Una varita AB de longitud l se mueve en el plano del diseño (fig. 17) de modo que en un momento de tiempo dado la dirección de la velocidad de su extremo A forma un ángulo α, y la velocidad del extremo B, un ángulo β con la varita. El valor de la velocidad del extremo A es v. Determinar el valor de la velocidad del extremo B. Encontrar la posición del eje fijo perpendicular al plano del diseño con relación al cual la varita gira en el momento de tiempo que se examina, (o sea, hallar la posición del eje instantáneo de rotación de la varita).
Solución:
La componente de la velocidad a lo largo de la varita para todos los puntos de ésta será única e igual a ![]() . Por consiguiente, la velocidad del extremo de la varita B es igual a
. Por consiguiente, la velocidad del extremo de la varita B es igual a![]() . El movimiento de la varita puedo analizarse como la suma del movimiento de avance a lo largo de AB con velocidad u y giratorio simultáneo alrededor del eje que es perpendicular al plano del diseño y que pasa por un punto O de la varita. La distancia del punto O hasta el extremo de la varita A puede determinarse fácilmente de la relación
. El movimiento de la varita puedo analizarse como la suma del movimiento de avance a lo largo de AB con velocidad u y giratorio simultáneo alrededor del eje que es perpendicular al plano del diseño y que pasa por un punto O de la varita. La distancia del punto O hasta el extremo de la varita A puede determinarse fácilmente de la relación
![]()
El movimiento de la varita, en un determinado momento de tiempo, también puede analizarse como movimiento giratorio alrededor del eje O’ que es perpendicular al plano del diseño y está situado en la perpendicular de OO’ a la AB. La distancia
OO’ será:
![]() .
.
Representar gráficamente la distribución de las velocidades a lo largo de la varita AB en las condiciones del problema anterior.
Solución:
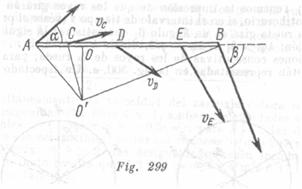
La distribución de las velocidades de diferentes puntos de la varita está representada en la fig. 299. La velocidad ![]() de un punto arbitrario C de la varita en magnitud es igual a
de un punto arbitrario C de la varita en magnitud es igual a
![]()
y está dirigida perpendicularmente a la recta trazada del punto O’ (véase el problema anterior) al punto dado C.
Muchas hormigas tiran de un pedazo de corteza del árbol que tiene forma de un triángulo equilátero. Se sabe que en cierto momento de tiempo la velocidad
del vértice B es igual a v y está dirigida a lo largo de la línea AB y la velocidad del vértice C tiene la dirección de la línea CB. Encontrar la velocidad del vértice
C en el mismo momento.
Solución:
![]()
Un coche de turismo va por una carretera horizontal tras de un camión. Entre los neumáticos dobles de las ruedas traseras del camión se atrancó una piedra ¿a que del camión deberá ir el coche a fin de que la piedra desprendida de las ruedas del camión no dé en el coche? Los dos automóviles van con una velocidad de 50km/h
Solución:
Este problema es más cómodo resolverlo usando un sistema de coordenadas relacionado al movimiento uniforme de los automóviles. En este sistema la carretera se mueve hacia atrás con velocidad ![]() los ruedas giran. La velocidad lineal de los puntos situados en la circunferencia de la rueda y la velocidad lineal de la piedra presa serán también iguales a v. la piedra recorrerá la distancia máxima, si se desprende las ruedas en el momento en que su velocidad forma con la horizontal un ángulo de
los ruedas giran. La velocidad lineal de los puntos situados en la circunferencia de la rueda y la velocidad lineal de la piedra presa serán también iguales a v. la piedra recorrerá la distancia máxima, si se desprende las ruedas en el momento en que su velocidad forma con la horizontal un ángulo de ![]() . Encontremos esta distancia. Despreciando la circunstancia de que automóviles están en reposo el uno respecto al otro y sus en el momento del desprendimiento la piedra se halla en un nivel mas alto que el nivel de la carretera, obtenemos la distancia máxima que es
. Encontremos esta distancia. Despreciando la circunstancia de que automóviles están en reposo el uno respecto al otro y sus en el momento del desprendimiento la piedra se halla en un nivel mas alto que el nivel de la carretera, obtenemos la distancia máxima que es![]() la distancia entre los automóviles no podrá ser menor que 19.6m.
la distancia entre los automóviles no podrá ser menor que 19.6m.
En la pantalla cinematográfica se proyecta un carruaje en movimiento. Los radios de las ruedas delanteras del carruaje son ![]() 0.35m y de las ruedas traseras
0.35m y de las ruedas traseras![]() , las ruedas delanteras tienen
, las ruedas delanteras tienen ![]() rayos. En una cámara de filtración la película gira con una velocidad de 24 cuadros por segundo. Al considerar que las ruedas del carruaje se mueven sin deslizamiento, determinar la velocidad mínima con la cual debe ir el carruaje para que los espectadores tengan la impresión de que las ruedas delanteras del carruaje en la pantalla están inmóviles. ¿Qué número mínimo de rayos
rayos. En una cámara de filtración la película gira con una velocidad de 24 cuadros por segundo. Al considerar que las ruedas del carruaje se mueven sin deslizamiento, determinar la velocidad mínima con la cual debe ir el carruaje para que los espectadores tengan la impresión de que las ruedas delanteras del carruaje en la pantalla están inmóviles. ¿Qué número mínimo de rayos ![]() deben tener en este caso las ruedas traseras paras que ellas también parezcan inmóviles?
deben tener en este caso las ruedas traseras paras que ellas también parezcan inmóviles?
Solución:
El ángulo entre los rayos vecinos de la rueda delantera es ![]() Para Un Espectador la rueda no girará, si en el intervalo de filmación de dos imágenes consecutivas
Para Un Espectador la rueda no girará, si en el intervalo de filmación de dos imágenes consecutivas ![]() ), ella gira en un ángulo
), ella gira en un ángulo ![]() donde
donde ![]() es un número entero positivo. Por otro lado, el ángulo de giro de la rueda en el intervalo de tiempo T es
es un número entero positivo. Por otro lado, el ángulo de giro de la rueda en el intervalo de tiempo T es ![]() , donde
, donde ![]() es la velocidad angular de la rueda. Por consiguiente, la rueda delantera parecerá estar inmóvil, si t°=
es la velocidad angular de la rueda. Por consiguiente, la rueda delantera parecerá estar inmóvil, si t°=![]() En estas condiciones, la velocidad del carruaje es
En estas condiciones, la velocidad del carruaje es ![]()
![]() este tendrá el valor mínimo igual
este tendrá el valor mínimo igual![]() a Las ruedas traseras también parecerán estar inmóviles, si
a Las ruedas traseras también parecerán estar inmóviles, si ![]()
![]() de donde obtenemos que para
de donde obtenemos que para
![]()
¿Para qué velocidades del movimiento del carruaje que va de izquierda a derecha (véase los datos del problema 62) los espectadores tendrán la impresión de que?:
1) los rayos de las ruedas giran en sentido antihorario?
2) los rayos de las ruedas delanteras y traseras giran en sentidos opuestos?
El número de los rayos de las ruedas delanteras y traseras es el mismo e igual a 6.
Solución:
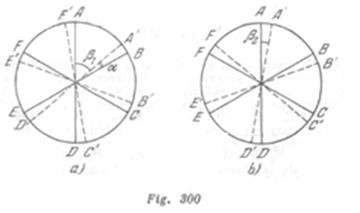
Tenemos la impresión de que los rayos girarán en sentido antihorario, si en el intervalo de tiempo T (véase el problema 62) la rueda gira en un ángulo P que satisface la siguiente condición ![]()
![]() donde k = 1,2,3…Las posiciones consecutivas de los rayos de la rueda, para este caso, están representadas en la figura 300 a Un espectador tendrá la impresión de que cada rayo giro en un ángulo impresión de que cada rayo giró en un ángulo
donde k = 1,2,3…Las posiciones consecutivas de los rayos de la rueda, para este caso, están representadas en la figura 300 a Un espectador tendrá la impresión de que cada rayo giro en un ángulo impresión de que cada rayo giró en un ángulo ![]() en sentido antihorario. Los valores posibles de la velocidad angular se encuentran, respectivamente, en el intervalo:
en sentido antihorario. Los valores posibles de la velocidad angular se encuentran, respectivamente, en el intervalo:
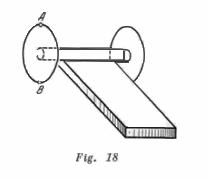
Una bobina que consta de la parte cilíndrica y de dos discos iguales y continuos rueda con una velocidad constante ![]() , sin deslizamiento mediante su parte cilíndrica por una barra áspera, colocada horizontalmente (fig. 18) el radio de la parte cilíndrica es
, sin deslizamiento mediante su parte cilíndrica por una barra áspera, colocada horizontalmente (fig. 18) el radio de la parte cilíndrica es![]() , de los discos es
, de los discos es ![]() . ¿Que velocidad tienen los puntos
. ¿Que velocidad tienen los puntos ![]() y
y ![]() que se encuentran en el diámetro exterior de uno de los discos?
que se encuentran en el diámetro exterior de uno de los discos?
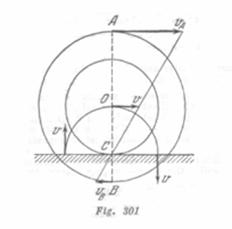
Solución:
Por el punto C (fig. 301) pasa el eje instantáneo de rotación (véase el problema 57). Por eso, el punto A tiene una velocidad
Igual a ![]() El punto
El punto![]() posee una velocidad
posee una velocidad
Igual a ![]()
¿Qué puntos de los discos (véase el problema anterior) tienen una velocidad instantánea, igual por su valor a la velocidad del eje de la bobina?
Solución:
La velocidad instantánea, igual a la velocidad del eje de la bobina, es la velocidad de los puntos situados en la circunferencia de radio ![]() , cuyo centro es el punto
, cuyo centro es el punto ![]()
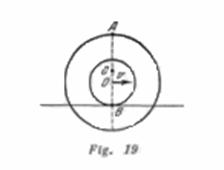
Trazar las trayectorias de los puntos ![]() ,
,![]() y
y ![]() de la bobina (fig. 19) que rueda mediante su parte cilíndrica por una barra sin deslizamiento.
de la bobina (fig. 19) que rueda mediante su parte cilíndrica por una barra sin deslizamiento.
Solución:
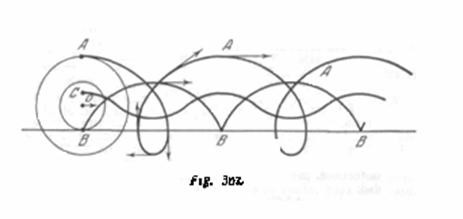
Las trayectorias de los puntos ![]() ,
,![]() y
y ![]() están representadas en la (fig.302) .El punto
están representadas en la (fig.302) .El punto ![]() describe una cicloide simple; los puntos
describe una cicloide simple; los puntos ![]() y
y![]() describe una cicloide alargada y reducida, respectivamente.
describe una cicloide alargada y reducida, respectivamente.
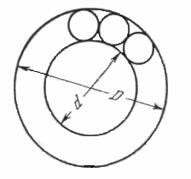
Un cojinete de bolas sostiene el externo del eje de un árbol que gira con velocidad angular![]() el diámetro del eje del árbol es
el diámetro del eje del árbol es ![]() (fig.20) y el del aro del cojinete es
(fig.20) y el del aro del cojinete es ![]() . Encontrar la velocidad lineal del movimiento del centro de una de las bolas si el aro es fijo y si este gira con velocidad angular
. Encontrar la velocidad lineal del movimiento del centro de una de las bolas si el aro es fijo y si este gira con velocidad angular![]() . Considerar que en ambos casos las bolas giran por el árbol y el aro sin deslizamiento.
. Considerar que en ambos casos las bolas giran por el árbol y el aro sin deslizamiento.
Solución:
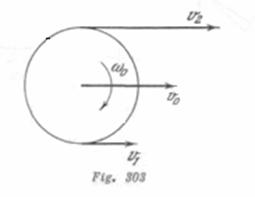
La velocidad lineal de los puntos en la circunferencia del árbol es ![]() . La velocidad lineal de los puntos del diámetro exterior es
. La velocidad lineal de los puntos del diámetro exterior es ![]() .Puesto que las bolas ruedan sin deslizamiento, las velocidades instantáneas de aquellos puntos de la bola, los cuales en un determinado momento tocan el árbol y el diámetro exterior, serán también iguales a
.Puesto que las bolas ruedan sin deslizamiento, las velocidades instantáneas de aquellos puntos de la bola, los cuales en un determinado momento tocan el árbol y el diámetro exterior, serán también iguales a ![]() . Pero la velocidad instantánea de cualquier punto de la bola puede ser considerada como la suma de dos velocidades: la velocidad del movimiento de su centro
. Pero la velocidad instantánea de cualquier punto de la bola puede ser considerada como la suma de dos velocidades: la velocidad del movimiento de su centro ![]() y la velocidad lineal del movimiento lineal del movimiento giratorio alrededor del centro. La rotación de la bola se realizara con cierta velocidad angular
y la velocidad lineal del movimiento lineal del movimiento giratorio alrededor del centro. La rotación de la bola se realizara con cierta velocidad angular ![]() (fig. 303). Por eso
(fig. 303). Por eso ![]() de donde
de donde ![]() .
.
En esta expresión cada una de las velocidades angulares pueden ser tanto positiva (rotación en sentido horario), como negativa (rotación en sentido antihorario). Para ![]() , tenemos que
, tenemos que
![]()
Un cono rueda sin deslizamiento por un plano. El eje del cono gira con una velocidad![]() en torno de la vertical que pasa por su vértice. La altura del cono es
en torno de la vertical que pasa por su vértice. La altura del cono es ![]() y el ángulo formado por el eje y la generatriz es
y el ángulo formado por el eje y la generatriz es ![]() . ¿Cuál es la velocidad angular de rotación del cono alrededor de su eje? Determinar la velocidad lineal de un punto arbitrario del diámetro de la base del cono situado en el plano vertical.
. ¿Cuál es la velocidad angular de rotación del cono alrededor de su eje? Determinar la velocidad lineal de un punto arbitrario del diámetro de la base del cono situado en el plano vertical.
Solución:
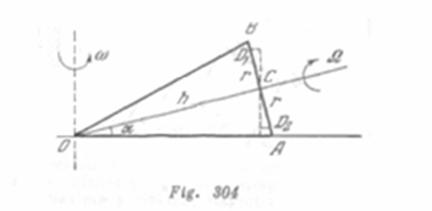
Como el cono rueda sin deslizamiento, los puntos de la generatriz ![]() (fig. 304) deben estar fijos. De esta condición se determina la velocidad
(fig. 304) deben estar fijos. De esta condición se determina la velocidad ![]() de rotación del cono en torno de su propio eje. Para el punto de esta condición obtenemos
de rotación del cono en torno de su propio eje. Para el punto de esta condición obtenemos![]() . La velocidad de un punto arbitrario
. La velocidad de un punto arbitrario ![]() del diámetro
del diámetro![]() de la base del cono se compone de dos velocidades:
de la base del cono se compone de dos velocidades:
![]()
Donde ![]() es la distancia del punto dado hasta el centro
es la distancia del punto dado hasta el centro ![]() de la base. Para un punto
de la base. Para un punto![]() , situado mas abajo del centro
, situado mas abajo del centro ![]() , tendremos:
, tendremos:
![]()
El punto extremo inferior tiene una velocidad nula y el punto extremo superior, una velocidad![]() .
.
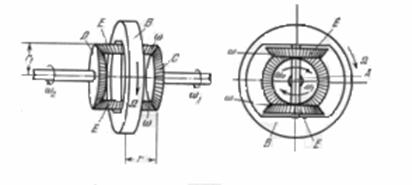
En la (fig. 21) está representada esquemáticamente la diferencial de un automóvil necesaria para que las ruedas del automóvil no deslicen al pasar por un sector curvilíneo del trayecto. (No obstante, las ruedas deben girar con diferentes velocidades.) El motor hace girar la rueda ![]() , con la que está rígidamente unido al eje
, con la que está rígidamente unido al eje ![]() . Alrededor del eje puede girar libremente un par de engranajes cónicos
. Alrededor del eje puede girar libremente un par de engranajes cónicos![]() . Este par de engranajes cónicos por los cuales este primero gira. El eje de las ruedas motrices del automóvil (como regla, las traseras) está cortado por el medio y en los extremos del eje están colocados los engranajes
. Este par de engranajes cónicos por los cuales este primero gira. El eje de las ruedas motrices del automóvil (como regla, las traseras) está cortado por el medio y en los extremos del eje están colocados los engranajes ![]() y
y ![]() . Estas mitades del eje pueden girar con diferentes velocidades angulares, siempre unidos con la diferencial. Hallar la relación entre las velocidades angulares
. Estas mitades del eje pueden girar con diferentes velocidades angulares, siempre unidos con la diferencial. Hallar la relación entre las velocidades angulares ![]() de la diferencial. Si los radios de los engranajes
de la diferencial. Si los radios de los engranajes ![]() son iguales a
son iguales a![]() y los radios de los engranajes
y los radios de los engranajes ![]() y
y ![]() son iguales a
son iguales a ![]()
Solución:
En los lugares de embargue de los engranajes cónicos![]() y
y![]() , así como de
, así como de ![]() y
y ![]() , las velocidades lineales deben ser iguales. Como el engranaje
, las velocidades lineales deben ser iguales. Como el engranaje ![]() gira alrededor del eje
gira alrededor del eje ![]() con velocidad
con velocidad ![]() y el propio eje gira en otro plano con velocidad
y el propio eje gira en otro plano con velocidad ![]() , entonces para el embargue de las ruedas
, entonces para el embargue de las ruedas![]() y
y ![]() tiene lugar la igualdad
tiene lugar la igualdad ![]() .
.
Para el embargue de las ruedas ![]() y
y ![]() se verifica la igualdad análoga siguiente:
se verifica la igualdad análoga siguiente:![]() . Resolviendo estas igualdades obtenemos
. Resolviendo estas igualdades obtenemos ![]() y
y  .
.
Para una velocidad determinada ![]() de la rueda
de la rueda ![]() , accionada por el motor, las velocidades angulares de las ruedas motrices del automóvil se diferenciaran la una de la otra en un valor que vario de cero hasta
, accionada por el motor, las velocidades angulares de las ruedas motrices del automóvil se diferenciaran la una de la otra en un valor que vario de cero hasta ![]()
Cuatro tortugas se encuentran en los ángulos de un cuadrado con lado![]() . Las tortugas empiezan a andar simultáneamente con una velocidad
. Las tortugas empiezan a andar simultáneamente con una velocidad![]() , constante por su magnitud, dirigiéndose la primera tortuga todos l tiempo a la segunda, la segunda a la tercera, la tercera a la cuarta y la cuarta a la primera.
, constante por su magnitud, dirigiéndose la primera tortuga todos l tiempo a la segunda, la segunda a la tercera, la tercera a la cuarta y la cuarta a la primera.
¿Se encontraran o nó las tortugas? Si se encuentran ¿después de cuánto tiempo ocurrirá esto?
Solución:

Partiendo de los conceptos de simetría, es evidente que, en cualquier momento de tiempo las tortugas estarán en los ángulos del cuadrado, cuyo lado disminuye todo el tiempo (fig. 305). La velocidad de cada tortuga puede descomponer en una velocidad radial (dirigida al centro) y en una velocidad perpendicular a la radial. La velocidad radial, o sea, la velocidad de aproximación al centro, será ![]() . Cada tortuga pasara hasta el centro una distancia
. Cada tortuga pasara hasta el centro una distancia ![]() . De este modo, las tortugas se encantaran en el centro del cuadrado dentro de un intervalo de tiempo
. De este modo, las tortugas se encantaran en el centro del cuadrado dentro de un intervalo de tiempo ![]() .
.
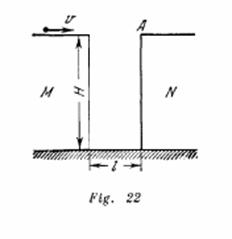
Desde un sector rectilíneo de la orilla salieron el mismo tiempo dos buques ![]() y
y![]() que inicialmente se encontrara en a una distancia
que inicialmente se encontrara en a una distancia ![]() el uno del otro. El buque
el uno del otro. El buque ![]() navegaba por una recta perpendicular a la orilla. El buque
navegaba por una recta perpendicular a la orilla. El buque![]() siempre mantenía el rumbo hacia el primer buque
siempre mantenía el rumbo hacia el primer buque![]() , teniendo en cada momento la misma velocidad que el buque
, teniendo en cada momento la misma velocidad que el buque ![]() . Es evidente que dentro de un intervalo del tiempo suficientemente grande el segundo buque irá detrás del primero, encontrándose a cierta distancia de éste último. Hallar esta distancia.
. Es evidente que dentro de un intervalo del tiempo suficientemente grande el segundo buque irá detrás del primero, encontrándose a cierta distancia de éste último. Hallar esta distancia.
Solución:
El buque![]() se mueve en dirección al buque
se mueve en dirección al buque ![]() con velocidad
con velocidad ![]() . Al mismo tiempo, el buque
. Al mismo tiempo, el buque ![]() se aleja del
se aleja del ![]() con velocidad
con velocidad![]() (fig. 306). De esta manera la distancia
(fig. 306). De esta manera la distancia ![]() disminuye con velocidad
disminuye con velocidad ![]() . El punto
. El punto ![]() (proyección del punto
(proyección del punto ![]() en la trayectoria del buque
en la trayectoria del buque ![]() ) se mueve con velocidad
) se mueve con velocidad ![]() . Como resultado, la distancia
. Como resultado, la distancia ![]() aumenta con velocidad
aumenta con velocidad![]() . Así, la suma de las distancias
. Así, la suma de las distancias ![]() pertenece constante durante el movimiento de los buques. En el movimiento inicial el punto
pertenece constante durante el movimiento de los buques. En el movimiento inicial el punto ![]() coincidía con el punto
coincidía con el punto ![]() y por eso
y por eso![]() . después de un intervalo suficientemente grande de tiempo, el punto
. después de un intervalo suficientemente grande de tiempo, el punto![]() coincidirá con el punto
coincidirá con el punto![]() . En esta condición tendremos
. En esta condición tendremos ![]() . Dos buques se moverán a una distancia de
. Dos buques se moverán a una distancia de ![]() el uno del otro.
el uno del otro.
Dos placas de acero![]() y
y ![]() de altura
de altura ![]() (fig. 22) están en la arena. La distancia entre las placas es
(fig. 22) están en la arena. La distancia entre las placas es![]() . Sobre la placa
. Sobre la placa ![]() rueda uniformemente una bola. Cuya velocidad
rueda uniformemente una bola. Cuya velocidad ![]() no se conoce exactamente. No obstante se sabe que esta velocidad está en el intervalo de
no se conoce exactamente. No obstante se sabe que esta velocidad está en el intervalo de ![]() a
a ![]() .
.
1) ¿Para qué altura ![]() no se puede predecir la dirección de la velocidad de la bola por la horizontal en el momento de su caída en la arena? (Hasta su caída en la arena la bola choco contra a placa
no se puede predecir la dirección de la velocidad de la bola por la horizontal en el momento de su caída en la arena? (Hasta su caída en la arena la bola choco contra a placa ![]() por lo menos una vez.)
por lo menos una vez.)
2) ¿Para qué altura mínima de las placas no se puede pronosticar el lugar de caída de la bola en el sector ![]() ? Menospreciar el tiempo de choque de la bola contra la placa. El choque se considera absolutamente elástico.
? Menospreciar el tiempo de choque de la bola contra la placa. El choque se considera absolutamente elástico.
Solución:

El movimiento de la bola puede examinarse como la suma d los movimientos por la vertical (uniformemente acelerado) y por la horizontal (movimiento uniforme).
La solución del problema se simplificará, si construimos el grafico de la dependencia de la coordenada da la bola a lo largo de la horizontal en función del tiempo para los valores limites de la velocidad de ![]() y
y ![]() (fig. 307). Las líneas quebradas inferior y superior corresponden a al velocidad de la bola máxima y mínima, respectivamente. Con el tiempo,
(fig. 307). Las líneas quebradas inferior y superior corresponden a al velocidad de la bola máxima y mínima, respectivamente. Con el tiempo,
Como se ve en el gráfico, la indeterminación de la coordenada ![]() de la bola, dada por el segmento de la recta horizontal, encerrada entre las líneas del gráfico, aumenta. El sombreado vertical en la (fig. 307) corresponde al movimiento de la bola de
de la bola, dada por el segmento de la recta horizontal, encerrada entre las líneas del gráfico, aumenta. El sombreado vertical en la (fig. 307) corresponde al movimiento de la bola de ![]() a
a ![]() y el horizontal corresponde al movimiento de
y el horizontal corresponde al movimiento de ![]() a
a ![]() . Las regiones de intersección de los sombreados corresponden a la indeterminación en dirección de la velocidad horizontal.
. Las regiones de intersección de los sombreados corresponden a la indeterminación en dirección de la velocidad horizontal.
1) Directamente del gráfico se deduce que la dirección de la velocidad de la bola por la horizontal, después de haber saltado una vez de la placa, será indeterminada para el tiempo de caída ![]() . Consecuentemente,
. Consecuentemente,![]() .
.
2) La bola podrá caer en cualquier punto de la base, sobre la cual están situadas las placas, si el tiempo de caída de la bola ![]() . Por lo tanto, .
. Por lo tanto, .
![]()
