- III.12.1 Ley fundamental de la inducción electromagnética é
1°. El fenómeno de inducción electromagnética consiste en que un contorno que se halla en un campo magnético alternativo, se genera un campo eléctrico inductivo. De medidas energética de este campo sirve la fuerza electromotriz εi de inducción electromagnética. Si el contorno es cerrado, por la acción del campo eléctrico inducido se produce en él la ordenación del movimiento de los electrones, es decir, una corriente eléctrica que se llama corriente de inducción.
2°. ley de la inducción electromagnética (ley de Faraday); la fem εi de la inducción electromagnética de un contorno es proporcional a la velocidad de la superficie de la limitación por este contorno:
 |
(en el SI) |
 |
(en el sistema de Gauss) |
Aquí no importa qué es lo que ocasiona la variación de flujo magnético: puede ser la deformación o el desplazamiento del contorno en un campo magnético externo o cualquier otra causa de la variación de ese campo en función del tiempo. Cuando un contorno conductor cerrado se traslada en un campo magnético, las fem se inducen en todos los sectores que cortan las líneas de inducción magnética del mismo. La suma algebraica de estas fem (p. 3°) es igual a la fem total del contorno. Para trasladar el contorno cerrado en el campo magnético, hay que realizar un trabajo equivalente a de la corriente de inducción engendrada en el contorno.
Al calcular 
y 
, los sentidos de recorrido del contorno (III.8.3.2°) y de la normal exterior n (III.10.2.5°, 6°) se coordinan de tal modo que desde el extremo del vector n se vea que el recorrido del contorno se efectúa en un sentido contrario al de las agujas del reloj. Si el contorno cerrado consta de N espiras en serie (por ejemplo un solenoide (III.10.3.7°)), en la ley de Faraday el flujo magnético se sustituye por el flujo magnético total ψ (III.10.6.5°):
 |
(en el SI) |
 |
(en el sistema de Gauss) |
3°. La fem de la inducción electromagnética en un contorno se considera positiva si el vector momento magnético Pm de la corriente de inducción (III.10.3.4°) que le corresponda forma un ángulo con líneas de inducción magnética del campo que induce esta corriente. En el caso contrario εi se considera negativa. En la fig. III.12.1.a la fem: 
<0, y en el caso representado en la fig. III.12.1, b, >0.
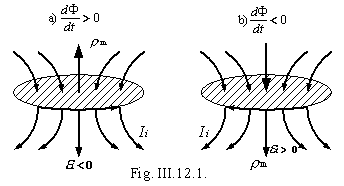
4°. El signo de la ley de inducción magnética se halla en correspondencia con la ley de Lenz; en toda variación del flujo magnético a través de una superficie limitada por un contorno cerrado, en este último surge una corriente de inducción
cuya dirección es tal, que su campo magnético se opone a que varíe el flujo magnético que produce dicha corriente.
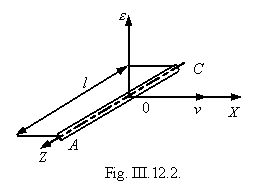
5°. La fem de inducción electromagnética surge en el sector del conductor que al moverse corta las líneas de inducción del campo magnético (III.10.1.3°). En el caso representado en la fig. III.12.2, sobre los electrones de conducción del metal (III.7.3.1°) actúa la fuerza de Lorentz (III.11.1.1°): FL= -e[(v+v’)B], en la que v es velocidad con que se mueve el vector AC del conductor en el campo magnético, cuyo vector inducción B es perpendicular al plano que pasa por el sector del conductor y por su velocidad de traslación. Los electrones se mueven ordenadamente a lo largo del conductor, con velocidad v’, bajo la acción de la componente de la fuerza de Lorentz tangente al conductor y dirigida desde A hacia C. el movimiento de los electrones cesa cuando el campo electroestático que aparece en el conductor y que ejerce sobre los electrones la fuerza eE, compensa la acción de la fuerza de Lorentz.
Según la ley de Ohm para circuito abierto (cuando I = 0) (III.8.2.5o), la diferencia de potencial de equilibrio
entre lo puntos A y C, la cual se establece cuando v’ = 0, constituye
donde 
es la fuerza electromotriz de inducción, puesto que en el sector AC no hay alguna fuente de energía eléctrica.
La fem de inducción electromagnética en un trozo de conductor de longitud l que se mueve con velocidad v constituirá
o bien
donde 
es la relación entre el flujo magnético a través de la superficie que barre el conductor al moverse durante un intervalo infinitesimal de tiempo, y la magnitud dt de este intervalo, en otras palabras, la velocidad con que el conductor corta las líneas de inducción del campo magnético (compare con III.12.1.2°).
6°. El fenómeno de inducción electromagnética en los conductores cerrados en reposo, que se encuentra en un campo magnético alternativo externo, no se puede explicar valiéndose de la fuerza de Lorentz, ya que ésta no actúa sobre las cargas en reposo (III.11.1.1°).
El fenómeno de inducción electromagnética en los conductores en reposo se explica por hecho de que el campo magnético alternativo contribuye a que aparezca un campo eléctrico rotacional. La circulación de la tensión de este campo a lo largo del contorno cerrado del conductor L (III.3.1.4°) es la fem de inducción magnética:
 |
(en el SI) |
 |
(en el sistema de Gauss) |
donde la diferencia parcial 
toma en consideración la variación del flujo magnético de inducción tan sólo en función del tiempo. Acerca de la elección del sentido de la normal n al calcular el flujo magnético, véase el p. 2°.
7°. La magnitud q de la carga eléctrica que pasa a través de la sección transversal de la espira del conductor en que se induce la corriente constituye
 |
(en el SI) |
 |
(en el sistema de Gauss) |
donde 
son los valores del flujo magnético a través del área de la espira en sus posiciones inicial y final, y R, la resistencia eléctrica de dicha espira.
- III.12.2. Fenómeno de autoinducción
1°. Se da el nombre de fenómeno de autoinducción al surgimiento de un campo eléctrico de inducción en un circuito a consecuencia de la variación en él de la intensidad de la corriente. La característica energética del campo generado es la fem de autoinducción 
.
2°. Respectivamente, el campo magnético de la corriente que pasa por el circuito genera un flujo magnético 
a través de la superficie 
limitada por el contorno con corriente,
donde 
es la proyección del vector inducción B del campo magnético (III10.1.2°) de la corriente sobre la normal n al elemento de superficie 
. La magnitud 
se llama flujo magnético de autoinducción de contorno. Aplicando l a ley de Biot-Savart-Laplace (III.10.2.2°) se puede calcular para el caso en que el contorno se encuentra en un medio no ferromagnético (III.13.5.2°):
 |
(en el SI) |
 |
(en el sistema de Gauss) |
 |
(en el SI) |
 |
(en el sistema de Gauss) |
o bien
donde L se denomina inductancia (inductancia estática) del contorno y se determina por las formulas siguientes:
 |
(en el SI) |
 |
(en el sistema de Gauss) |
En estas formulas 
q es la constate magnética en el SI (III.10.2.2°); , la permeabilidad magnética relativa del medio; r, el radio vector trazado desde el elemento 
del contorno hasta el elemento 
de la superficie S limitada por este contorno; y el subíndice n indica que es la proyección sobre la normal al elemento .
3°. La inductancia del contorno L equivale numéricamente al flujo de autoinducción cuando la intensidad de la corriente 
(en el SI); I = c (en el sistema de unidad de Gauss). La inductancia L depende solamente de la forma geométrica y de la dimensiones del contorno, así como las propiedades magnéticas del medio en que el se encuentre.
La inductancia de un solenoide bastante largo (III.4.3.7°) constituye
 |
(en el SI) |
 |
(en el sistema de Gauss) |
4°. De la ley de Faraday (III.12.1.2°) se deduce la expresión de la fem de autoinducción:
 |
(en el SI) |
 |
(en el sistema de Gauss) |
Para un contorno indeformable que se halla en un medio no ferromagnético (III.13.5.2°). L= const., por lo que
 |
(en el SI) |
 |
(en el sistema de Gauss) |
5°. La fuerza electromagnética de autoinducción es la causa de que en el contorno surja corriente de autoinducción que, según la ley de Lenz (III.12.1.4°), se opone a que varíe la intensidad de la corriente principal en el circuito, frenando tanto su disminución como su aumento. La medida de la inercia del contorno respecto de la variación en él de la intensidad de la corriente es la inductancia de ese contorno (p. 3°).
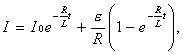
6°. La ley de variación de la intensidad de la corriente eléctrica en un circuito al cerrarlo o abrirlo, es decir, con régimen transitorio, constituye
donde I0 es la intensidad de la corriente en el instante inicial 
; R, la resistencia eléctrica del circuito; L, su inductancia; y 
la suma algebraica de las fem de las fuerzas de energía eléctrica intercaladas en el circuito (III.8.2.2°).
Al conectar la fuente de fem, en el circuito no hay corriente inicial :
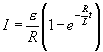
La intensidad de la corriente en el circuito aumenta desde
cero hasta el valor de 
correspondiente a la magnitud de la
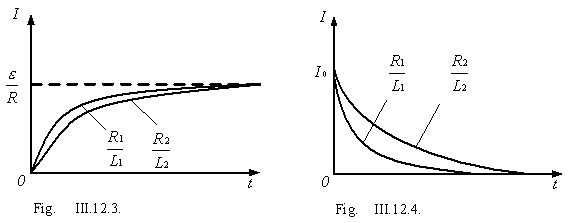
Intensidad de la corriente continúa. Este aumento es tanto mas rápido cuando mayor es la relación 
(fig. III.12.3).
Al desconectar la fuente de fem,
La intensidad de la corriente en el circuito disminuye exponencialmente desde su valor inicial I0, y esta disminución es tanto más rápida cuando mayor es la relación 
(fig. III.12.4).
- III.12.3. Inducción mutua
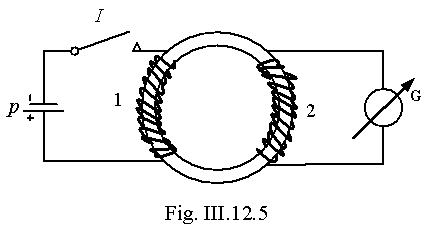
1o. Si cerca de un circuito de corriente alterna hay conductores, en ellos se genera una fem de inducción. En esto consiste el fenómeno de inducción mutua. Por lo tanto si en el circuito 1 (fig. III.12.5) varía la intensidad de la corriente I1, en el circuito 2 se genera una fem de autoinducción 
,
 |
(en el SI) |
 |
(en el sistema de Gauss) |
donde 
es el flujo magnético a través de la superficie del contorno del segundo circuito, debido al campo magnético de la corriente que pasa por el primer circuito (flujo magnético de inducción mutua).
2o. Por analogía con (III.2.2.2o) el flujo magnético 
es proporcional a la intensidad I1:
 |
(en el SI) |
 |
(en el sistema de Gauss) |
donde 
recibe el nombre de inductancia mutua (inductancia mutua estática) de los contornos segundo y primero. La magnitud depende de la forma, las dimensiones y disposición mutua de ambos contornos, así como de la permeabilidad magnética relativa del medio en que se encuentran. El flujo magnético 
a través de la superficie del contorno del primer circuito, debido al campo magnético de la corriente I2 que pasa por el segundo circuito, constituye
 |
(en el SI) |
 |
(en el sistema de Gauss) |
donde 
es la inductancia mutua de los contornos primero y segundo.
Si los contornos se hallan en un medio no ferromagnético (III.13.5.2°), M21=M12 para un medio ferromagnético. Las inductancia mutuas M21=M12 no son iguales entre sí y dependen de los factores antes enumerados y, además, de los valores de las intensidades de las corrientes en ambos contornos y del carácter de las variaciones de dichas corrientes.
3°. Las expresiones de la fem. de inducción mutua, a condición de que M21=M12 son:
 |
(en el SI) |
 |
(en el sistema de Gauss) |
 |
(en el SI) |
 |
(en el sistema de Gauss) |
- III.1.12.4. Energía del campo magnético de la corriente eléctrica
1o. Para crear corriente eléctrica en un contorno cerrado y aumentar su intensidad desde cero hasta I hay que realizar un trabajo A para vencer la fem dee autoinducción que se opone al incremento de la corriente (III.12.2.6o),
 |
(en el SI) |
 |
(en el sistema de Gauss) |
donde es el flujo magnético de autoinducción del contorno (III.12.2.2o), y , la inductancia de este último (III.12.2.2o).
Según la ley de conservación de la energía, A determina la energía intrínseca Wm de la intensidad de la corriente I en el contorno:
 |
(en el SI) |
 |
(en el sistema de Gauss) |
2o. Al mismo tiempo que la intensidad de la corriente, en el circuito también crece el campo magnético de ésta. Por esto la energía intrínseca de la corriente se considera como energía del campo magnético. Por ejemplo, para un solenoide largo (III.10.3.8o), cuyo campo magnético es uniforme (III.10.1.2o),
 |
(en el SI) |
 |
(en el sistema de Gauss), |
siendo V el volumen del solenoide; n, el numero de espiras por unidad de longitud; 
, la constante magnética (III.10.2.2o); y 
la permeabilidad magnética relativa del medio.
3o. La densidad volumétrica de la energía 
de un campo magnético es la energía de éste encerrada en la unidad de volumen del mismo.
Para un campo magnético uniforme (III.10.1.3o), 
. La densidad volumétrica de cualquier campo magnético, incluso si no es uniforme, viene expresada por la fórmula:
 |
(en el SI) |
 |
(en el sistema de Gauss) |
aquí B y H son los módulos de los vectores inducción magnética (III.10.1.2o) e intensidad (III.10.2.3o), en el punto que se considera del campo magnético. Las demás notaciones véanse en el p. 2o. :
4o.la energía 
del campo magnético localizado en el volumen V constituye.
 |
(en el SI) |
 |
(en el sistema de Gauss) |
5o. Si el campo magnético es generado por un sistema arbitrario de n contornos cuyas intensidades de la corriente son I1,I2,I3,…In, la energía de este campo se puede expresar por medio de la formula del p. 4o, en la cual B y H son los módulos de los vectores B y H del campo magnético resultante, de acuerdo con el principio de superposición de los campos (III.2.2.2o). Además, en este caso la energía del campo magnético se puede representar mediante la formula:
 |
(en el SI) |
 |
(en el sistema de Gauss) |
donde
es el flujo magnético total “embragado” al k-enésimo contorno (III.10.6.5o). Al calcular este flujo, la normal 
, a la superficie que se extiende sobre el contorno, se traza de tal modo que desde el extremo del vector 
se vea que la corriente pasa por el contorno en sentido inverso al de las agujas del reloj. El flujo magnético
donde 
es el flujo magnético de autoinducción de k-enésimo contorno (III.12.2.2o), y 
el flujo magnético de su inducción mutua originada por los campos magnéticos de todos los demás contornos con corriente (III.12.3.1o). De acuerdo con esto, la energía del campo magnético 
será
 |
(en el SI) |
 |
(en el sistema de Gauss) |
El primer termino representa la suma de las energías intrínsecas de todas las corrientes (p.1o). El segundo término se llama energía mutua de las corrientes. En él Mk es la inductancia mutua de los contornos k-enésimo y L-enésimo (III.12.3.2o) cuyas respectivas corrientes son 
.
Colaboración de los estudiantes: |
|
| Mauricio Armando Rivera Mogollón | |
| Mariela Margarita Campo | |
| Luís Fernando Ospino Campo | |