Electromagnetismo – Capitulo 13 – Materiales magnéticos en un campo magnético.

§ III.13.1.  Momentos magnéticos de los electrones y de los átomos 

     1°. Se llaman magnéticos los materiales capaces de adquirir, un campo magnético externo, propiedades magnéticas, o sea, imanar y crear su propio campo magnético. Las propiedades magnéticas de una substancia vienen determinadas por las de sus electrones y átomos. Con arreglo a las propiedades magnéticas, los cuerpos se dividen en tres grupos principales: diamagnéticos (III.13.3.1°), paramagnéticos (III.13.4.1°) y ferromagnéticos (III.13.6.1°).

     2°. El movimiento de un electrón por su orbita en un átomo (VI.2.1.9°), equivale a cierto circuito cerrado con corriente (corriente orbital). De acuerdo con (III.10.3.4°), el momento magnético orbital del electrón Pm constituye:

Donde I = ev es la intensidad de la corriente; e, la magnitud absoluta de la carga del electrón; v, el número de vueltas del electrón por la orbita en la unidad de tiempo; S, el área de la orbita del electrón; n, el vector unidad de la normal a la superficie S; y c, la constante electrodinámica (III.10.2.2°).

Un electrón que se mueve describiendo una orbita, posee momento de impulso orbital Le    (I.4.1.4°). El momento magnético orbital es proporcional al momento de impulso orbital:

Donde

La magnitud g se llama razón giromagnética de los mementos orbitales. En las ultimas formulas, m es la masa del electrón; e, la magnitud absoluta de su carga; y c, la constante electrodinámica (III.10.2.2°). Los vectores Pm y Le tienen sentidos opuestos y son perpendiculares al plano de la orbita del electrón.

     3°. El electrón posee un momento de impulso propio Le, llamado espín del electrón. La magnitud absoluta del espín del electrón es

en la que h es la constante de Planck (IX), y h = .

Una peculiaridad importantísima del espín del electrón es la de tener solamente dos proyecciones sobre la dirección del vector B de inducción del campo magnético:

      4°. Al espín del electrón Les le corresponde un momento magnético de espín P_ms, que es proporcional al espín y cuyo sentido es inverso al de éste:

La magnitud g_s recibe el nombre de razón giromagnética de los momentos de espín:

El significado de estas notaciones véase en el p. 2. La proyección del momento magnético de espín del electrón P_ms B sobre la dirección del campo magnético (p. 3) es:

Donde µ_B es el magnetón de Bohr, que es la unidad de medida de los momentos magnéticos (IX).

     5°. Lo dicho en los pp. 1-4 es correcto para cada uno de los Z electrones del átomo. El número Z coincide con el de orden que ocupa el elemento químico en el sistema periódico de  Mendeléiev (VI.2.3.5°).

Se denomina momento magnético orbital Pm de un átomo, la suma vectorial de los momentos magnéticos orbitales Pm  de todos sus electrones:

Se da el nombre de momento de impulso orbital L de un átomo, a la suma vectorial de los momentos de impulso orbitales Le de los Z electrones:

Entre los momentos atómicos Pm y L existe la relación

P_m = gL,

En la que g es la razón giro magnética (p. 2°).

§ III.13.2. átomo del campo magnético

     1°. Si una substancia se encuentra en un campo magnético externo, dentro de los límites de un átomo se puede considerar que el campo magnético es uniforme (III.10.1.2°). Esto se deduce de la pequenez de las dimensiones lineales del átomo. Supongamos que un electrón se mueve en el átomo describiendo una órbita circular cuyo plano es perpendicular al vector inducción B del campo magnético. La acción que ejerce sobre el electrón la fuerza de Lorente FL  (III.11.1.1°) hace que disminuya la fuerza con que el electrón es atraído por el núcleo. La fuerza centrípeta (I.2.4.3°) resulta ser igual a la diferencia F_e – F_L, en la que F_e es la fuerza de Coulomb (III.1.2.2°) con que el núcleo atrae el electrón. Como resultado de esto varia la velocidad angular (I.1.5.3°) del movimiento del electrón por la órbita circular.

     2°. La variación de la velocidad angular del movimiento del electrón se produce durante el proceso de crecimiento del campo magnético en que se introduce el átomo. El aumento del campo magnético que actúa sobre este último se efectúa en un tiempo finito. Con esto se produce un campo eléctrico rotacional inducido (III.12.1.1°) que actúa sobre el electrón en el átomo. La intensidad E de este campo está dirigida según la tangente a la órbita del electrón, y la fuerza que actúa sobre el electrón es

F = eE (III.2.1.2°).

     3°. Si la orbita del electrón está orientada arbitrariamente respecto al vector B, el momento magnético orbital Pm , de ese electrón (III.13.1.2°) formará un ángulo α con la dirección experimentará cierta procesión alrededor de la dirección del vector B (I.4.3.2°). Esto significa que el vector P_m, perpendicular al plano de la órbita, conservando invariable el ángulo α de inclinación respecto al campo, girará alrededor de la dirección de B con velocidad angular L:

Aquí e es la magnitud absoluta de la carga del electrón; m, su masa; H, la intensidad del campo magnético; c, la constante electrodinámica (III.10.2.2°); y L recibe el nombre de velocidad angular de precisión de Larmor.

Teorema de Larmor: el único resultado de la influencia del campo magnético sobre la órbita del electrón en el átomo es la precisión de dicha órbita y del vector P_m, con velocidad angularL alrededor del eje que pasa por el núcleo del átomo, y es paralelo al vector B de inducción del campo magnético.

     4°. El movimiento de precisión de la órbita hace que aparezca la corriente orbital adicional   y el momento magnético orbital inducido  correspondiente a ella, cuyo modulo es

donde S es el área de la proyección de la órbita del electrón sobre un plano perpendicular a la dirección del vector B. El vector ΔP_m está dirigido en sentido contrario al del vector inducción magnética B:

El momento orbital inducido total ΔPm del átomo (III.13.1.5°) constituye:

donde Z es el número de electrones que tiene el átomo, y 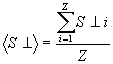 es el área media de las proyecciones de las órbitas de los electrones del átomo sobre el plano perpendicular a la dirección del vector B.

§ III.13.3 Diamagnéticos y paramagnéticos en un campo magnético uniforme.

     1°. La imanación o magnetización de una substancia se caracteriza por el vector magnetización (intensidad de magnetización) J, entendiéndose por éste la relación entre el momento magnético de un volumen pequeno ΔV de la substancia y el valor de dicho volumen:

,

donde P_mi  es el momento magnético del i-ésimo átomo (o molécula), y N, el número total de átomos (o moléculas) que hay en el volumen pequeno ΔV. Dentro de los límites del volumen ΔV, el campo magnético se considera  uniforme. Al mismo tiempo, en este volumen deberá haber un número bastante grande de partículas N (N>>1), para que tenga sentido el valor medio de las magnitudes físicas que caracterizan el sistema de dichas partículas.

     2°. Se llaman diamagnéticas aquellas substancias en las que los momentos magnéticos de los átomos (o moléculas), en ausencia de campo magnético externo, son iguales a cero. Esto significa que en los cuerpos diamagnéticos, la suma vectorial de los momentos magnéticos orbitales de todos los electrones del átomo es nula (III.13.1.5°), y que solamente en presencia de campo magnético existen momentos magnéticos inducidos (III.13.2.4°).

     3°. En el volumen ΔV de diamagnético isótropo, los momentos inducidos ΔP_m de todos los átomos (o moléculas) son iguales y están dirigidos en sentido contrario al del vector B (III.13.2.4°).

El vector magnetización

O teniendo en cuenta (III.13.2.4°):

Siendo n₀ el número de átomos (o moléculas) que hay en la unidad de volumen. El significado de las demás notaciones véase en III.13.2.3°. Llamado

Tenemos que

donde X’m es una magnitud adimensional que caracteriza las propiedades magnéticas de los materiales magnéticos. Para todos los diamagnéticas de los materiales magnéticos. Para todos los diamagnéticos X’m < 0.

     4°. Recibe el nombre de susceptibilidad magnética Xm la magnitud entre cuyo valor y X’m existe la relación

donde

En la práctica, para los diamagnéticos Xm = X’m, ya que la magnitud absoluta de X’m es muy pequena:

     5°. Se llaman paramagnéticas las substancias  en las cuales los átomos (o las moléculas), en ausencia de campo magnético externo, poseen cierto momento magnético Pm permanente. Esto significa que la suma vectorial de los momentos magnéticos orbitales de todos los electrones del átomo (o molécula) es distinta de cero (III.13.1.5°).

     6°. Cuando una sustancia paramagnética se introduce en un campo magnético uniforme (III.10.1.2°), los momentos magnéticos permanentes de los átomos (o moléculas) experimentan cierta precesión alrededor de la dirección del vector B de inducción del campo magnético, con una velocidad angular de Larmor L (III.13.2.3°).

El movimiento térmico y las colisiones entre los átomos (o moléculas) del cuerpo paramagnético contribuyen al amortiguamiento de la precesión de los momentos magnéticos, disminuyendo los ángulos entre las direcciones de los vectores de los momentos magnéticos y la dirección del vector B. la acción conjunta de las colisiones interatómicas y el campo magnético hace que la orientación predominante de los momentos magnéticos de los átomos sea en sentido del campo externo. Aunque el momento magnético permanente  P_m de un átomo (o molécula) es de un orden de magnitud de 10^-23 J/T (10^-20 erg/Gs), los momentos magnéticos de todas las partículas en la unidad de volumen engendra una magnetización que supera mucho los fenómenos diamagnéticos (p. 3). En una substancia paramagnética situada en un campo magnético externo existe un campo magnético propio dirigido a lo largo del campo magnético externo.

     7°. En la teoría clásica del paramagnetismo, el modulo del vector magnetización (p. 1) se expresa por medio de la formula

En la que n₀ es el número de átomos (o moléculas) que hay en la unidad de volumen, y L (a), la función clásica de Langevin:

El parámetro a tiene la forma . Aquí B es la inducción del campo magnético; K, la constante de Boltzmann (II.1.4.5°); y T, la temperatura absoluta. A la temperatura ambiente y con campos externos no muy intensos, a << 1 y la función L (a), después de desarrollarla en serie, se simplifica: L (a)  .

Con esto el vector magnetización

donde X’m se halla por la formula

La magnitud X’m se relaciona con la susceptibilidad magnética Xm por medio de las formulas del p. 4. Los valores de la magnitud X’m para los cuerpos paramagnéticos son positivos y se encuentran entre los límites de 10^-5 a 10^-3, por lo que X’m = Xm con alto grado de exactitud.

     Ley de Curie: la susceptibilidad paramagnética de una substancia es inversamente proporcional a la temperatura absoluta.

En los campos magnéticos externos muy intensos se llega a la saturación de imanación: cuando a >> 1, la función de Langevin L (a) → 1. Esto quiere decir que los momentos magnéticos de todos los átomos (o moléculas) están orientados a lo largo del campo magnético externo y

§ III.13.4. Campo magnético de los cuerpos magnéticos

     1°. En una substancia se distinguen dos tipos de corrientes generadas por el campo magnético: las macrocorrientes y las microcorrientes. Se llaman macrocorrientes las corrientes de conducción (III.7.1.2°) y las de convección (III.7.1.2°). Las microcorrientes (corrientes moleculares) son las debidas al movimiento de los electrones dentro de los átomos, moléculas y iones.

El campo magnético de un cuerpo es la suma vectorial de dos campos (III.2.2.2°): el campo magnético externo generado por las macrocorrientes, y el campo magnético intrínseco o campo magnético propio generado por las microcorrientes. El vector inducción magnética B (III.10.1.2°) del campo magnético de la substancia, caracteriza el campo magnético resultantes y es igual a la suma geométrica de las inducciones magnéticas de los campos magnéticos externo B₀ e intrínseco B_int:

Las fuentes primarias del campo magnético de los cuerpos magnéticos son las macrocorrientes. Sus campos magnéticos son los que ocasionan la imanación de la substancia situada en el campo magnético externo.

     2°. La ley de la corriente total para el campo magnético de una substancia es la generalización de la ley formulada en (III.10.5.2°):

Donde I_macro   e  I _micro son las sumas algebraicas de las macro y microcorrientes a través de la superficie que se extiende sobre el circuito cerrado L.

     3°. Entre la suma algebraica de las fuerzas de las microcorrientes y el vector magnetización existe la relación.

donde es la circulación del vector magnetización J (III.13.3.1°) a lo largo del circuito cerrado L que abarca las microcorrientes.

La ley de la corriente total (p. 2°) tiene en definitiva la forma

     4°. El vector

se llama intensidad del campo magnético existen en un medio cualquiera. La ley de la corriente total para el campo magnético en un medio arbitrario se escribe de forma idéntica a (II.10.5.4°):

Sustituyendo (1 – X’m) ó (1- 4X’m), basándose en (III.13.3.4°), tenemos:

donde

La magnitud µ así introducida  recibe el nombre de  permeabilidad magnética relativa de la substancia. En estas fórmulas, Xm es la susceptibilidad magnética (III.13.3.4°).

§ III.13.5. Ferromagnéticos

     1°. Se llama ferromagnéticos los cuerpos en los cuales el campo magnético intrínseco (III.13.4.1°) es centenares y millares de veces mayor que el campo magnético externo que lo genera.

El ferromagnetismo se observa en los cristales de los metales de transición (VI.2.3.8°), tales como el hierro. El cobalto y el níquel, así como en una serie de aleaciones, a condición de que se cumpla la desigualdad  en la que d es el diámetro del átomo,  de su capa electrónica incompleta (VI.2.3.6°).

     2°. Las propiedades fundamentales de los ferromagnéticos que los distinguen de los otros tipos de materiales magnéticos son:

1. Las dependencia de la imanación (III.13.3.2°) respecto de la intensidad H del campo magnético externo se caracteriza por la existencia de la saturación magnética Js, que comienza cuando .
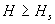2. La dependencia de la inducción magnética B respecto de H se distingue porque la misma aumenta, según una ley lineal, cuando .
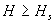3. La dependencia de pa permeabilidad magnética relativa µ respecto de la intensidad H tiene carácter complejo.
4. La existencia de la histéresis magnética de los ferromagnéticos, o sea, del retraso con que varía la imanación respecto de la variación de la intensidad del campo magnetizante externo, alternativo en magnitud y sentido. Este retraso se explica por la dependencia de J respecto de la “prehistoria” de la imanación de la substancia.
5. Las propiedades antes enumeradas de los cuerpos ferromagnéticos se ponen de manifiesto a temperaturas inferiores al punto de Curie 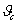. A temperaturas 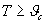, el movimiento térmico destruye tanto la región e imanación espontánea (p. 4) como el ferromagnético, y, perdiendo sus peculiaridades, éste se transforma en substancia paramagnética (III.13.3.5). El punto de Curie para el hierro es 1043 K; para el níquel, 631K; para el cobalto, 1043 K; y para la aleación permalloy, 823 K.

     3°. Se llama bucle de histéresis de imanación de un ferromagnético sometido a un campo magnético externo, al variar la intensidad de este campo desde + H_shasta H_s y viceversa, siendo H_s la intensidad del campo correspondiente a la saturación magnética. La magnitud ± J_s de la imanación, cuando H = ± H_s, se llama imanación de saturación. La cantidad de imanación ± J_R que se conserva en el ferromagnético en ausencia de campo exterior (cuando H = 0) recibe el nombre  de imanación remanente o remanencia. La existencia de J_R sirve de base para la creación de imanes permanentes. La intensidad ± H_s del campo exterior que desimana totalmente la substancia se denomina fuerza coercitiva (intensidad retardante).

La fuerza coercitiva determina la propiedad del ferromagnético de conservar la imanación remanente. Posee gran fuerza coercitiva los materiales magnéticos “duros”que proporcionan un bucle de histéresis ancho y que se utilizan para fabricar imanes permanentes. Tienen poca fuerza coercitiva los materiales magnéticos“blandos” que ofrecen un bucle de histéresis estrecho y que se emplean para fabricar núcleos de transformadores.

La reimanación de un ferromagnético está relacionada con el cambio de orientación de las regiones de magnetización espontánea (p. 4) y requiere la realización de trabajo a expensas de la energía del campo magnético exterior. La cantidad de calor que se desprende durante la reimanación es proporcional al área del bucle de histéresis.

     4°. A temperaturas inferiores al punto de Curie, el ferromagnético se divide en pequenas regiones de magnetización espontánea uniforme, llamadas dominios. Las dimensiones lineales de los dominios son del orden (10^-5 – 10^-4) m. Dentro de cada dominio la substancia está imanada hasta la saturación. En ausencia de campo magnético  externo, los momentos magnéticos de los distintos dominios están orientados en el espacio de tal modo que el momento magnético resultante de todo cuerpo ferromagnético es nulo.

Bajo la influencia del campo magnético exterior, en el ferromagnético se efectúa la orientación de los momentos magnéticos no de las partículas aisladas, como en el caso de los paramagnéticos (III.13.3.6°), sino de los dominios enteros. Como resultado de esto, la substancia se imana.

Las propiedades ferromagnéticas sólo pueden tenerlas los cuerpos en estado cristalino en que  la interacción entre los átomos vecinos de la red conduce a la energía total del sistema de electrones que asegura el cumplimiento de las condiciones de existencia del ferromagnetismo (III.13.5.1°).

     5°. La medida de la razón giromagnética  (III.13.1.4°) para los cuerpos ferromagnéticos ha demostrado que los portadores elementales del magnetismo en los ferromagnéticos son los momentos magnéticos de espín de los electrones (III.13.1.4°). En la teoría mecano cuántica moderna del ferromagnetismo se explica la naturaleza de la magnetización espontánea de los ferromagnéticos y las causas de que se produzca el intenso campo intrínseco (III.13.4.1°).

Poseen propiedades ferromagnéticas los cristales de las substancias cuyos átomos tienen capas y subcapas internas no completamente ocupadas por electrones (VI.2.3.6°) cuyo momento de espín resultante proporciona un valor distinto de cero de su proyección sobre la dirección del campo magnético (III.13.1.3°). Entre los espines de estos electrones se produce una interacción mecano cuántica especial, de procedencia no magnética, llamada interacción de cambio (VI.2.1.4°). Como resultado de esto, el estado del sistema de electrones en los ferromagnéticos, cuando los espines están orientados paralelamente, resulta ser estable, produciéndose la magnetización espontánea y originándose un fuerte campo magnético intrínseco.

Colaboración:
Ever Atencia Arenas
Jairo Andrés Bermúdez