¿Posee la cantidad de movimiento un disco homogéneo que gira en torno de su eje? El eje del disco está fijo.
Solución:
Dividimos la masa del disco en pares de segmentos iguales que se encuentran en el mismo diámetro y equidistantes del centro. La cantidad de movimiento de cada par es igual a cero, ya que las cantidades de movimiento de ambas masas son iguales, pero dirigidas en sentidos opuestos. Por consiguiente, la cantidad de movimiento de todo el disco es igual a cero.
Dos canoas navegan paralelamente, la una al encuentro de la otra, con velocidades iguales. Cuando las canoas se encuentran, de una lancha a la otra lanzan una carga, después de la segunda lancha a la primera lanzan una carga igual. Otra vez las cargas fueron lanzadas de una canoa a la segunda simultáneamente. ¿En que caso la velocidad de las canoas, después de lanzar la; cargas, será mayor?
Solución:
Supongamos que la masa de la canoa sea 
la de la carga 
y la velocidad inicial de las canoas 
. Al lanzar la carga de la canoa, sobre la última actúa una fuerza perpendicular a . No obstante, la variación de la cantidad de movimiento de la canoa no tendrá lugar, porque la fuerza de resistencia del agua impide el movimiento transversal de las canoas. La cantidad de movimiento de la canoa cambiará solamente por la caída de; la carga en ella. Aplicando la ley de conservación de la cantidad de movimiento en el sistema canoa-carga, en primer caso podemos escribir:
Para una canoa,
Para otra canoa.
y 
son las velocidades finales de las canoas. Del sistema de ecuaciones dado obtenemos
En el caso cuando las cargas se lanzan simultáneamente, las velocidades finales de las canoas y se determinarán de las siguientes ecuaciones:
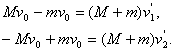
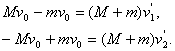
Resolviendo el sistema, recibimos 
De esto modo, la velocidad final de las canoas en el primer caso será mayor.
Una rana de masa está sentada en el extremo de un tabla de masa y de longitud 
. La tabla está flotando en la superficie de un lago. La rana salta a lo largo de la tabla, formando un ángulo 
con la horizontal ¿Qué velocidad inicial debe tener la rana para que, al dar un salto, se encuentre en el otro extremo de la tabla?
Solución:
La cantidad de movimiento del sistema tabla-rana en dirección horizontal no cambia. Por consiguiente podemos escribir
Donde 
es la velocidad de la tabla respecto a la superficie inmóvil del lago. A fin de que la rana alcance el otro extremo de la tabla, deberá satisfacerse la siguiente condición:
Donde 
es el tiempo durante el cual la rana se encuentra en el aire; este tiempo es 
De las ecuaciones existentes podemos determinar 
Una cuña con el ángulo de base se encuentra en una mesa horizontal lisa. Por el plano inclinado de la cuña sube un escarabajo con una velocidad constante respecto a la cuña. Determinar la velocidad de la cuña. Considerar que el escarabajo comenzó a moverse cuando la cuña estaba en reposo. La masa de la cuña es y la masa del escarabajo es .
Solución:
Considerando que en dirección horizontal el sistema escarabajo – cuña está cerrado, para determinar la velocidad 
de la cuña podemos usar el principio do conservación de la cantidad de movimiento
Donde
es la componente horizontal de la velocidad del escarabajo respecto a un sistema de referencia inmóvil.
De ahí recibimos 
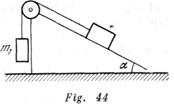
Una cuña, cuyo ángulo de base es , puede desplazarse sin fricción por una superficie horizontal lisa (fig. 44). ¿Para qué relación de masas
y 
de las cargas, unidas por medio de una cuerda apoyada sobre una polea, la cuña permanecerá inmóvil, y para qué relación de cargas la cuña se moverá hacia la derecha o hacia la izquierda? El coeficiente de fricción entre la carga 
y la cuña es 
Solución:
Como no existen las fuerzas externas que actúan sobre el sistema en dirección horizontal, la proyección de la cantidad de movimiento total del sistema cuña — cargas en dirección horizontal continuará constante (igual a cero). De ahí se deduce que la cuña comenzará a moverse sólo en el caso de movimiento de las cargas. Para que la carga se mueva hacia la derecha debo satisfacerse la siguiente condición:
de donde 
Para esta condición la cuña se desplazará hacia la izquierda. A fin de que la carga 
se mueva hacia la izquierda, debe verificarse la siguiente condición:
Ó 
En este caso la cuña se moverá hacia la derecha. Por consiguiente, para el equilibrio de la cuña la relación de masas de las cargas deberá satisfacer la siguiente desigualdad
A lo largo de un plano inclinado liso, cuyo ángulo con la horizontal es 
, comenzó a deslizarse con velocidad inicial nula, una caja con arena de masa 
. Después de recorrer la distancia 
, la caja chocó con una piedra de masa
, que se movía en dirección horizontal. ¿Qué velocidad tenía la piedra si la caja con arena después del choque paró un momento? Las velocidades de la piedra y de la caja se encuentran en el mismo plano.
Solución:
Para la dirección a lo largo del plano inclinado podemos escribir
donde es la velocidad de la caja en el momento cuando la piedra alcanza esta caja. Esta velocidad es igual a 
Por lo tanto,
Un cohete lanzado verticalmente hacia arriba explotó en la altura máxima de su ascenso. Como resultado de la explosión, el cohete se dividió en tres pedazos. Demostrar que los vectores de las velocidades iniciales de los tres pedazos se hallan en el mismo plano.
Solución:
En el punto máximo de ascenso del cohete su velocidad es nula. La variación de la cantidad de movimiento total de los fragmentos del cohete, bajo la acción de las fuerzas externas (fuerza de la gravedad), es muy insignificante, ya que el impulso de estas fuerzas es muy pequeño debido a la corta duración de la explosión. Por lo tanto, la cantidad de movimiento total de los fragmentos del cohete, antes y después de la explosión, permanece constante e igual a cero. Sin embargo, los tres vectores 
tendrán la resultante nula solamente si ellos están situados en el mismo plano. De ahí concluimos vectores 
se encuentran en el mismo plano.
En la superficie de un lago hay una canoa, situada perpendicularmente a la línea de la orilla y que tiene su proa dirigida a la misma. La distancia entre la proa de la canoa y la orilla es igual a
En el momento inicial la canoa estaba inmóvil. El hombre que se encuentra en la canoa, pasa de la proa a la popa. ¿Atracará la canoa a la orilla, si su longitud es de
La masa de la canoa es 
y la masa del hombre es 
Solución:
La velocidad de la canoa respecto a la orilla se relaciona con la velocidad del hombre respecto a la canoa mediante la relación:
La relación de las velocidades durante el movimiento permanece constante. Como resultado de ello, la relación de los trayectos recorridos será igual a la relación de las velocidades:
donde es el camino recorrido por la canoa 
y es la longitud de la canoa (distancia recorrida por el hombre respecto a la canoa). Por consiguiente a fin de que la canoa atraque, su longitud no puede ser menor que 
La canoa no atracará.
De los extremos de una plataforma inmóvil de longitud 
un adulto y un niño corren el uno al encuentro del otro. Determinar en cuánto se desplazará la plataforma, cuando el hombre cubra la distancia de un extremo al otro. Es sabido que el adulto corre dos veces más rápido que el niño. La masa de la plataforma es 
, la masa del hombre es 
y la del niño es 
Solución:
Tomemos como origen de las coordenadas el punto de donde el adulto comenzó su movimiento. Entonces la coordenada inicial del centro de masas será:
Designemos por 
la coordenada del centro de masas en el momento cuando el adulto alcanza el extremo de la plataforma.
Entonces
donde 
es el desplazamiento de la plataforma. Puesto que el sistema adulto-niño-plataforma en dirección horizontal está cerrado, entonces 
De esta igualdad encontramos:
De los valores numéricos dados obtenemos que 
En un plano horizontal absolutamente liso se encuentra un aro. Sobre este último está un escarabajo. ¿Qué trayectoria describirán el escarabajo y el centro del aro si el escarabajo empezará a moverse a lo largo del aro? La masa del aro es , el radio 
y la masa del escarabajo es
Solución:
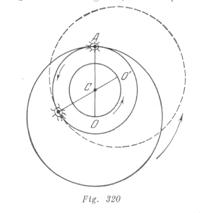
Las fuerzas externas no actúan en dirección horizontal del sistema aro – escarabajo. Por eso el centro de gravedad del sistema (punto
en la fig. 320) no se desplazará en el plano horizontal. La distancia entre el centro de gravedad del sistema y el centro del aro es
Como esta distancia es constante el centro del aro 
describirá, con relación al punto inmóvil , una circunferencia de radio 
Se puede verificar con facilidad que la trayectoria del escarabajo tiene la forma de una circunferencia de radio 
La posición recíproca, así como la dirección del movimiento del escarabajo y del aro se muestran en la fig. 320.
En el momento inicial el cohete de masa 
tenía una velocidad 
. Al final de cada segundo, el cohete desprende una porción de gas de masa 
. La velocidad de la porción de gas se diferencia de la velocidad del cohete, antes de que esta masa de gas sea quemada, en una magnitud constante , o sea, la velocidad de flujo del gas es constante. Menospreciando la acción de la fuerza de gravedad, determinar la velocidad del cohete después de n segundos.
Solución:
Designemos por 
la velocidad del cohete al final del 
-ésimo segundo. Al final del ésimo segundo el cohete lanza el gas de masa 
que lleva consigo una cantidad de movimiento 
Del principio de conservación de la cantidad de movimiento se deduce que
El cambio de la velocidad del cohete en
es igual a
Conociendo el cambio de la velocidad en se puede encontrar la expresión para la velocidad al final del enésimo segundo:
¿Aumentará la velocidad del cohete si la velocidad de flujo de los gases con relación al cohete es menor que la velocidad del mismo cohete, es decir, los gases, que salen de la tobera del cohete, van tras del cohete?
Solución:
La velocidad del cohete aumentará. Esto se hace evidente, si adoptamos un sistema de referencia respecto al cual el cohete, en un momento determinado, estará en reposo. La presión de los gases escapados empujará el cohete hacia adelante.
Un cañón de masa M que se mueve solamente por la horizontal, dispara bajo un ángulo a un proyectil de masa m con velocidad . Considerando como velocidad inicial del proyectil respecto a la tierra o al cañón, el ángulo de inclinación como el ángulo de inclinación del vector de la velocidad inicial o el ángulo de inclinación del tubo del cañón, encontrar la velocidad v de retroceso del cañón para todas las cuatro variantes.
Solución:
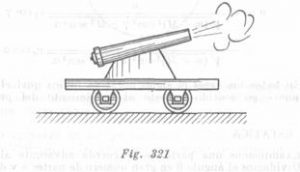
Para analizar todas las cuatro posibilidades, designemos por 
la velocidad inicial del proyectil respecto al cañón; por 
, la velocidad inicial del proyectil respecto a la tierra; por 
, el ángulo de inclinación del ánima del cañón; por 
, el ángulo de inclinación del vector de la velocidad inicial (fig. 321).
Las relaciones entre los valores indicados se determinan por las siguientes igualdades:
(1)
(2)
(3)
Consideremos 
como la velocidad inicial del proyectil con relación a la tierra y 
como el ángulo de inclinación del vector (o sea
,), entonces de la ecuación (3) obtenemos:
Luego consideremos como la velocidad inicial del proyectil respecto al ánima del cañón que está dirigido bajo un ángulo a con relación al horizonte (
). De esta manera, de las ecuaciones (1) y (3) recibimos
Si se da la velocidad inicial respecto a la tierra y el ángulo de inclinación del cañón (
), entonces tenemos que
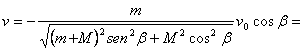
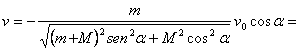
Por último, si es la velocidad inicial con relación al ánima del cañón y se conoce el ángulo de inclinación del vector de velocidad inicial respecto a la tierra (ángulo inicial de la trayectoria), recibimos
. Entonces resulta que
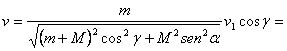
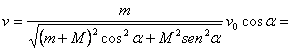
En todos los casos el signo negativo indica que el cañón se mueve en sentido opuesto al movimiento del proyectil.
Solución al ejercicio 113:
Como no existen las fuerzas externas que actúan sobre el sistema en dirección horizontal, la proyección de la cantidad de movimiento total del sistema cuña — cargas en dirección horizontal continuará constante (igual a cero). De ahí se deduce que la cuña comenzará a moverse sólo en el caso de movimiento de las cargas. Para que la carga 
se mueva hacia la derecha debo satisfacerse la siguiente condición:
de donde 
Para esta condición la cuña se desplazará hacia la izquierda. A fin de que la carga se mueva hacia la izquierda, debe verificarse la siguiente condición:
Ó 
En este caso la cuña se moverá hacia la derecha. Por consiguiente, para el equilibrio de la cuña la relación de masas de las cargas deberá satisfacer la siguiente desigualdad
