- I.1.1. Movimiento mecánico. Objeto de la mecánica
1°. La forma más simple de movimiento que hay en la naturaleza es el movimiento mecánico, que consiste en la variación de la posición recíproca de los cuerpos o de sus partes en el
espacio en el transcurso del tiempo. La parte de la física que se ocupa del estudio de las leyes del movimiento mecánico se llama mecánica. En un sentido más estrecho de la. palabra, se suele entender por mecánica la mecánica clásica, en la cual se estudian los movimientos de los cuerpos macroscópicos que se efectúan con velocidades muchísimo menores que la velocidad de la luz en el vacío. La base de la mecánica clásica son las leyes de Newton. Por esto también suele dársele el nombre de mecánica newtoniana. Las leyes del movimiento de los cuerpos con velocidades próximas a la de a luz en el vacío son objeto del estudio de la mecánica relativista (1.5.1.1°), y las leyes del movimiento de las micropartículas (por ejemplo, de los electrones en los átomos, moléculas, cristales, etc.) lo son de la mecánica cuántica (VI. 1.1.1°).
2°. La mecánica clásica tiene tres partes principales: estática, cinemática y dinámica. En la estática se estudian las leyes de la composición de las fuerzas y las condiciones de equilibrio de los cuerpos. En la cinemática se da la descripción matemática de todos los tipos posibles de movimiento mecánico sin relacionarla con! las causas que determinan cada tipo concreto de movimiento. En la dinámica se analiza la influencia de las interacciones entre los cuerpos sobre su movimiento mecánico.
3°. Las propiedades mecánicas de los cuerpos se determinan por su naturaleza química, estructura interna y estado, cuyo estudio no es objeto de la mecánica, sino de otras partes de la física. Por esto, para describir los cuerpos móviles reales de acuerdo con las condiciones de cada problema concreto, se utilizan en la mecánica diversos modelos simplificados: el punto material, el cuerpo rígido o sólido invariable, el cuerpo perfectamente elástico, el cuerpo plástico o absolutamente inelástico, etc.
Se llama punto material un cuerpo cuya forma y dimensiones carecen de importancia en las condiciones del problema dado. Por ejemplo, el movimiento de un buque de un punto a otro se puede considerar en primera aproximación como movimiento de un punto material. Pero en el caso en que sea necesario tener en cuenta un «detalle» de este movimiento, como el balanceo del barco cuando el mar está agitado, el buque debe considerarse como cuerpo extenso de forma determinada. En la literatura, en vez de «punto material» suele llamarse simplemente «punto».
Cualquier cuerpo extenso o sistema de cuerpos de este tipo que formen un sistema mecánico que se haya de investigar puede considerarse como un sistema de puntos materiales. Para esto todos los cuerpos del sistema deben dividirse mentalmente en un número de partes tan grande, que las dimensiones de cada una de ellas sean despreciables por su pequenez en comparación con las dimensiones de los mismos cuerpos.
4°. Se da el nombre de cuerpo rígido o sólido invariable a aquél, cuyas deformaciones pueden despreciarse en las condiciones de un problema dado. La distancia entre dos puntos cualesquiera de un cuerpo rígido no varía sean cuales fueran las acciones que se ejerzan sobre él. El cuerpo rígido se puede considerar como un sistema de puntos materiales rígidamente unidos entre sí.
Se llama cuerpo perfectamente elástico aquel, cuya deformación se subordina a la ley de Hooke (VII. 1.3.4°). Una vez que cesa la acción del esfuerzo exterior, este cuerpo recupera totalmente sus dimensiones iniciales y su forma.
Se dice que un cuerpo es absolutamente inelástico o plástico si, cuando cese la acción de la fuerza exterior, conserva totalmente el estado deformado provocado por dicha acción.
- I.1.2. Sistema de referencia. Trayectoria,espacio recorrido y vector traslaciónde un punto
1°. La posición de un cuerpo en el espacio sólo puede determinarse con respecto a otros cuerpos. Por ejemplo, tiene sentido hablar de la posición de los planetas con respecto al Sol;
de un avión o de una motonave con respecto a la Tierra, pero no puede indicarse su posición en el espacio «en general», sin relacionarla con cualquier cuerpo concreto. El cuerpo rígido, con el cual está asociado invariablemente un sistema de coordenadas provisto de relojes, que se utiliza para determinar la posición en el espacio de los cuerpos y partículas que se estudian en diferentes instantes, se llama sistema de referencia. A veces se llama sistema de referencia al mismo sistema de coordenadas provisto de relojes, y el cuerpo rígido del cual es solidario se denomina cuerpo de referencia. En cada problema concreto el sistema de referencia se elige de tal modo que simplifique lo más posible su solución. En física se utilizan generalmente sistemas de referencia inerciales (1.2.1.2°).
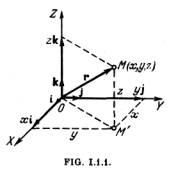
2°. El sistema de coordenadas que más se usa es el cartesiano rectangular (fig. I.l.l)/Cuya base ortonormalizada está constituida por tres vectores’unitarios por el módulo y recíprocamente ortogonales i, j y k, trazados desde el origen de coordenadas O. La posición de un punto arbitrario M se caracteriza por el radio vector r que une el origen de coordenadas O con el punto M. El vector r se puede descomponer según la base i, j, k:
![]()
donde xi, yj y zk son las componentes del vector r a lo largo de los ejes de coordenadas. Los coeficientes de descomposición x, y, son las coordenadas cartesianas del punto M y también, en virtud de la ortogonalidad de los vectores de la base, las proyecciones del radio vector r sobre los correspondientes ejes de coordenadas.
El movimiento de un punto material estará completamente determinado si se dan las tres funciones continuas y unívocas del tiempo t:
![]()
definen la variación de las coordenadas del punto con el tiempo.
Estas ecuaciones se llaman ecuaciones cinemáticas del movimiento del punto. Son equivalentes a la ecuación vectorial del movimiento del punto: r = r (t).
3°. La línea que describe en el espacio un punto en movimiento se llama trayectoria de dicho punto. Las ecuaciones cinemáticas del movimiento del punto dan la ecuación de su trayectoria en forma paramétrica (el parámetro es el tiempo t). En dependencia de la forma de la trayectoria, el movimiento del punto puede ser rectilíneo o curvilíneo. El movimiento del punto se dice que es plano, si su trayectoria se encuentra total mente en un plano.
El movimiento mecánico de un cuerpo es relativo, es decir, su carácter y, en particular, la forma de las trayectorias de los puntos de dicho cuerpo dependen del sistema de referencia que se elija.
4°. En el caso general, la trayectoria de un punto material no es plana, sino una curva espacial. Para-esta curva se introduce el concepto de plano osculador. Se llama plano osculador en un punto arbitrario M de una curva, la posición límite del plano que pasa por tres puntos cualesquiera de la curva cuando estos tres puntos sé aproximan ilimitadamente al punto M. Recibe el nombre de círculo osculador en un punto M de una
curva, el límite de la circunferencia que pasa por tres puntos de la curva considerada cuando estos tres puntos se aproximan ilimitadamente al punto M. El círculo osculador se encuentraen el plano osculador. El centro del círculo osculador y su radio se llaman respectivamente centro de curvatura y radio de curvatura de la curva correspondiente en el punto M. La recta que une el punto M con el centro de curvatura se llama normal principal a la curva en el punto M. La tangente a la curva en el punto M es perpendicular a la normal principal en este punto y también se encuentra en el plano osculador.
5°. El espacio recorrido por un punto es la suma de las longitudes de todos los tramos de la trayectoria recorridos por este punto en el intervalo de tiempo que se considere. El instante t = t0 antes del cual el movimiento no se estudia, se llama instante inicial, y la posición del punto en este instante (punto A en la fig. 1.1.2), posición inicial. En virtud del modo arbitrario en que se elige el punto de referencia del tiempo, se suele suponer que t0 = 0. El espacio s recorrido por el punto desde su posición inicial es una función escalar del tiempo: s = s (t) y, como se ve por la misma definición, el espacio recorrido por el punto no puede ser una magnitud negativa. Si el punto se mueve por un arco de trayectoria AB (fig. 1.1.2) siempre en la misma dirección y en un instante t se encuentra en el punto M, entonces![]() En cambio, si el punto se mueve por la trayectoria de un modo más complejo, por ejemplo, en el instante t1 < t se traslada de A a B y después, moviéndose en sentido contrario, en el instante í retorna al punto M, será
En cambio, si el punto se mueve por la trayectoria de un modo más complejo, por ejemplo, en el instante t1 < t se traslada de A a B y después, moviéndose en sentido contrario, en el instante í retorna al punto M, será![]()
6°. Se llama vector traslación de un punto en un intervalo de tiempo entre t = fj y t = í2, el vector trazado desde la posición del punto en el instante ít a su posición en el instante í2. Este vector es igual al incremento del radio vector del punto durante el espacio de tiempo considerado,![]()
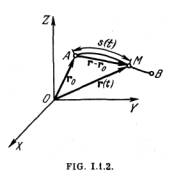
El vector traslación siempre está dirigido a lo largo de la cuerda que une los extremos del tramo de la trayectoria correspondiente.
En la fig. 1.1.2 se muestra el vector traslación del punto en el intervalo de tiempo entre t0 y t, igual a r — r0 = r (t) — r (t 0)
El vector traslación del punto en el lapso de t a t + Dt es igual a
![]()
donde Dx, Dy y Dz son los incrementos (variaciones) de las coordenadas del punto durante el intervalo de tiempo considerado.
7°. Un punto material, moviéndose libremente en el espacio, sólo puede efectuar tres movimientos independientes, es decir, tales que cada uno de ellos no puede representarse en forma de combinación de los demás. En efecto, el movimiento del punto a lo largo de cada uno de los ejes del sistema de coordenadas rectangulares cartesianas no puede realizarse a expensas de su movimiento a lo largo de los otros dos ejes. El número de movimientos independientes que puede efectuar un sistema mecánico se llama número de grados de libertad de este sistema. Así, pues, un punto material libre tiene tres grados de libertad.
§ I.1.3. Velocidad
1°. Para caracterizar la rapidez del movimiento de los cuerpos se introduce en mecánica el concepto de velocidad. Se llama velocidad media de un punto en movimiento en un intervalo de ![]()
tiempo de t a![]() el vector vmed igual a la razón del incremento
el vector vmed igual a la razón del incremento ![]() del radio vector del punto durante este intervalo de tiempo, a su duración Dt:
del radio vector del punto durante este intervalo de tiempo, a su duración Dt:
![]()
El vector vmed tiene la misma dirección que ![]() , es decir, a lo largo de la cuerda que une los extremos del tramo de trayectoria correspondiente.
, es decir, a lo largo de la cuerda que une los extremos del tramo de trayectoria correspondiente.
2°. Velocidad (o velocidad instantánea) de un punto es una magnitud vectorial v igual a la primera derivada respecto del tiempo del radio vector r del punto que se considera:
![]()
La velocidad de un punto en un instante t es igual al límite de la velocidad media vmed cuando la duración del intervalo Dt disminuye ilimitadamente
![]()
El vector v, velocidad del punto, está dirigido según la tangente a la trayectoria en el sentido del movimiento, lo mismo que el vector dr = v dt de una pequena traslación del punto en un intervalo de tiempo muy pequeno dt.
El espacio ds recorrido por el punto en un tiempo dt es igual al módulo del vector traslación: ds = | dr| . Por esto el módulo del vector velocidad del punto es igual a la primera derivada del espacio recorrido respecto del tiempo:
![]()
3°. La descomposición del vector v según la base de un sistema de coordenadas cartesianas rectangulares tiene la forma:
![]()
La proyección de la velocidad del punto sobre los ejes de coordenadas es igual a las primeras derivadas respecto del tiempo de las correspondientes coordenadas del punto:
![]()
y el módulo del vector velocidad
![]()
4°. Si el movimiento del punto es rectilíneo, la dirección de su vector velocidad permanece invariable. Se dice que el movimiento del punto es uniforme si el módulo de su velocidad no varía con el tiempo: v = ds/dt = const. Cuando el movimiento del punto es uniforme, el espacio s recorrido por él depende linealmente del tiempo: s = vt (con la condición de que t0 = 0, véase 1.1.2.5°).
Si el módulo de la velocidad del punto aumenta con el tiempo (dv/dt > 0), el movimiento se llama acelerado, y si disminuye (dv/dt < 0), se denomina retardado.
5°. Se da el nombre de velocidad absoluta media del movimiento variado de un punto en un tramo determinado de su trayectoria, a la magnitud escalar vmed igual a la razón de la longitud Ds de este tramo de trayectoria, al tiempo Dt que tarda el punto en recorrerlo:
![]()
Esta velocidad es igual al módulo del vector velocidad de un movimiento uniforme tal, que en recorrer este mismo espacio tarde el punto el mismo tiempo que con el movimiento variado.
Cuando el movimiento del punto es curvilíneo | Dr | < Ds. Por esto, en el caso general, la velocidad absoluta media de vmed no es igual al módulo de la velocidad media del punto vmed en este mismo tramo de trayectoria (1.1.3.1o): vmed ![]() | vmed|, donde el signo igual corresponde a la parte rectilínea de latrayectoria.
| vmed|, donde el signo igual corresponde a la parte rectilínea de latrayectoria.
6°. En el caso del movimiento plano de un punto M (1.1.2.3°) conviene frecuentemente utilizar las coordenadas polares r y ![]() , donde r es la distancia desde el polo O hasta el punto M, y
, donde r es la distancia desde el polo O hasta el punto M, y![]() , el ángulo polar medido desde el eje polar OA (fig. 1.1.3). La velocidad v del punto M se puede descomponer en dos componentes perpendiculares entre sí: la velocidad radial vr y la velocidad tangencial v
, el ángulo polar medido desde el eje polar OA (fig. 1.1.3). La velocidad v del punto M se puede descomponer en dos componentes perpendiculares entre sí: la velocidad radial vr y la velocidad tangencial v ![]() :
:
![]()
siendo
![]()
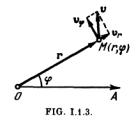
Aquí r es el radio vector polar de punto M, y k, el vector unitario dirigido perpendicularmente al plano del movimiento del punto, de forma que desde su extremo se vea efectuarse la rotación del vector r, al aumentar el ángulo polar![]() , en sentido contrario al de las agujas del reloj.
, en sentido contrario al de las agujas del reloj.
El módulo del vector velocidad v de un punto M que realiza un movimiento plano:
![]()
Durante un tiempo pequeno dt el radio vector polar r del punto que realiza el movimiento plano barre un sector circular de área![]() . Por esto la magnitud
. Por esto la magnitud
![]()
se llama velocidad sectorial.
§ I.1.4. Aceleración
1°. Para caracterizar la rapidez con que varía el vector velocidad de un punto se introduce en mecánica el concepto de aceleración. Se llama aceleración media de un punto en un intervalo de tiempo de t a ![]() el vector amed igual a la razón del incremento:
el vector amed igual a la razón del incremento:![]() del vector velocidad del punto en este lapso, a la duración
del vector velocidad del punto en este lapso, a la duración![]() de dicho intervalo:
de dicho intervalo:
![]()
2°. Aceleración (o aceleración instantánea) de un punto es la magnitud vectorial a igual a la primera derivada respecto del tiempo de la velocidad v del punto considerado o, lo que es lo mismo a la segunda derivada respecto del tiempo del radio vector, r de dicho punto:
![]()
La aceleración del punto en un instante t es igual al límite de la velocidad media amed cuando la duración del intervalo Dt disminuye ilimitadamente:
![]()
3°. Descomposición del vector a según la base de un sistema de coordenadas cartesianas rectangulares:
![]()
Las proyecciones de la aceleración sobre los ejes de coordenadas son iguales a las primeras derivadas respecto del tiempo de las correspondientes proyecciones de la velocidad o, lo que es lo mismo, a las segundas derivadas respecto del tiempo de las correspondientes coordenadas del punto:
![]()
El módulo del vector aceleración
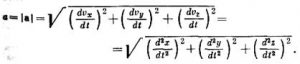
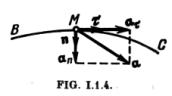
4°. El vector aceleración del punto se encuentra en el plano sculador (1.1.2.4°) que pasa por el punto considerado M de la trayectoria, y está dirigido hacia la parte cóncava de la misma, BC (fig. 1.1.4). En este plano el vector aceleración a se puede descomponer en las dos componentes perpendiculares entre sí:
![]()
5°. La componente aT se llama aceleración tangencial del punto y está dirigida según la tangente a la trayectoria del punto
![]()
donde ![]() es el vector tangencial unidad trazado por el punto M de la trayectoria en la dirección de la velocidad v del punto, y aT es la proyección de la aceleración tangencial sobre la dirección del vector v. La aceleración tangencial caracteriza la rapidez con que varía el módulo del vector velocidad del punto.
es el vector tangencial unidad trazado por el punto M de la trayectoria en la dirección de la velocidad v del punto, y aT es la proyección de la aceleración tangencial sobre la dirección del vector v. La aceleración tangencial caracteriza la rapidez con que varía el módulo del vector velocidad del punto.
Los vectores![]() y v coinciden por su dirección, es decir,
y v coinciden por su dirección, es decir, ![]() , cuando el
, cuando el
movimiento del punto es acelerado (I.1.3.4°); los vectores at y v tienen la misma dirección y sentios opuestos, o sea, at < 0, cuando el movimiento del punto es retardado, y at = 0, cuando su movimiento es uniforme. Si at = const y diferente de cero, el movimiento se llama uniformemente variado. Cuando el movimiento es uniforme, el módulo de la velocidad del punto depende linealmente del tiempo:
![]()
donde v0 = v (0) es el módulo de la velocidad inicial, es decir, de la velocidad en el instante inicial t = 0. Si at = const > 0, el movimiento del punto se dice que es uniformemente acelerado, y si at = const < 0, el movimiento del punto se denomina uniformemente retardado.
6°. La componente an de la aceleración a se llama aceleración normal del punto. Está dirigida según la normal principal a la trayectoria en el punto M considerado y hacia el centro de curvatura de la trayectoria (1.1.2.4°). Por esto an suele llamarse también aceleración centrípeta del punto. La aceleración normal
![]()
donde n es el vector unidad de la normal principal, y R es el radio de curvatura de la trayectoria. La aceleración normal caracteriza la rapidez con que varía la dirección del vector velocidad del punto.
Si el punto se mueve rectilíneamente, la aceleración normal an = 0 y la aceleración del punto es igual a su aceleración tangencial:
![]() .
.
§ I.1.5. Movimiento de traslación y de rotación de un sólido
1°. Se llama movimiento de traslación de un sólido aquel, durante el cual cualquier recta asociada rígidamente a dicho sólido (por ejemplo, la recta AB, de la fig. 1.1.5) se traslada permaneciendo paralela a su dirección inicial (A0B0). Tienen movimiento de traslación con respecto a la Tierra, por ejemplo, la cabina de un ascensor, la cuchilla de un torno, la aguja de una brújula cuando su caja se desplaza en un plano horizontal, etc.
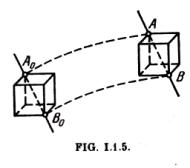
Cuando un sólido se traslada, todos sus puntos se desplazan exactamente lo mismo: en un tiempo pequeno dt, los radios vectores de estos puntos varían en una misma magnitud dr. Respectivamente, en cada instante todos los puntos del sólido tienen la misma velocidad, igual a dr/dt, y, por consiguiente, también son iguales sus aceleraciones. Por esto el estudio cinemático del movimiento de traslación de un sólido se reduce al estudio del movimiento de cualquiera de sus puntos. En la dinámica se estudia el movimiento del centro de inercia del sólido
(1.2.3.3°). Todo cuerpo sólido que se mueve libremente en el espacio tiene tres grados de libertad de traslación (1.1.2.7°), que corresponden a sus traslaciones a lo largo de los tres ejes de coordenadas.
2°. El movimiento de un sólido durante el cual dos de sus puntos A y B permanecen fijos, se llama rotación (o movimiento de rotación) del sólido alrededor de un eje fijo. La recta en reposo AB recibe el nombre de eje de rotación del sólido. Al girar alrededor del eje fijo, todos los puntos del sólido describen circunferencias, cuyos centros se encuentran en el eje de rotación y cuyos planos son perpendiculares a él. Este tipo de movimiento, con respecto a la Tierra, lo efectúan, por ejemplo, los rotores de las turbinas, de los motores eléctricos y de los generadores sujetos a ella.
El sólido que gira alrededor de un eje fijo sólo tiene un grado de libertad (1.1.2.7°). Su posición en el espacio se determina totalmente por el valor ![]() del ángulo de rotación a partir de una posición determinada (inicial).
del ángulo de rotación a partir de una posición determinada (inicial).
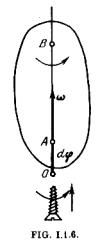
3°. Para caracterizar la rapidez y el sentido de la rotación del sólido alrededor del eje sirve la velocidad angular. Se llama velocidad angular el vector o, igual numéricamente a la primera derivada del ángulo de rotación![]() , respecto del tiempo t, y dirigido a lo largo del eje de rotación fijo, de tal modo que desde su extremo se vea que el sólido gira en sentido contrario al de las agujas del reloj (fig. 1.1.6) *):
, respecto del tiempo t, y dirigido a lo largo del eje de rotación fijo, de tal modo que desde su extremo se vea que el sólido gira en sentido contrario al de las agujas del reloj (fig. 1.1.6) *):
![]()
Aquí![]() es el vector rotación elemental (pequena) del sólido durante el tiempo dt, dirigido a lo largo del eje de rotación de acuerdo también con la regla del tornillo (fig. 1.1.6).
es el vector rotación elemental (pequena) del sólido durante el tiempo dt, dirigido a lo largo del eje de rotación de acuerdo también con la regla del tornillo (fig. 1.1.6).
Los vectores axiales ![]() y
y ![]() no tienen puntos de aplicación determinados: pueden tomarse desde cualquier punto del eje de rotación. En la fig. 1.1.6 están trazados desde cierto punto O del eje de rotación fijo, el cual se toma al mismo tiempo como origen de coordenadas del sistema de referencia.
no tienen puntos de aplicación determinados: pueden tomarse desde cualquier punto del eje de rotación. En la fig. 1.1.6 están trazados desde cierto punto O del eje de rotación fijo, el cual se toma al mismo tiempo como origen de coordenadas del sistema de referencia.
*) La dirección del vector![]() puede determinarse también por la regla del tornillo: dicha dirección coincide con la del movimiento de avance de un tornillo roscado a derechas que se mueva junto con el sólido. Los vectores semejantes al
puede determinarse también por la regla del tornillo: dicha dirección coincide con la del movimiento de avance de un tornillo roscado a derechas que se mueva junto con el sólido. Los vectores semejantes al![]() , cuya dirección está relacionada con el sentido de una rotación y se invierte al pasar del sistema de coordenadas dextrórsum al sistema de coordenadas sinestrórsum, se llaman seudovectores o vectores axiales (para diferenciarlos de los ordinarios o vectores polares, que no cambian de sentido cuando sé efectúa la transformación de coordenadas antedicha). Por ejemplo, el producto vectorial de dos vectores polares es un seudovector, mientras que el producto vectorial de un seudovector por un vector polar es un vector polar.
, cuya dirección está relacionada con el sentido de una rotación y se invierte al pasar del sistema de coordenadas dextrórsum al sistema de coordenadas sinestrórsum, se llaman seudovectores o vectores axiales (para diferenciarlos de los ordinarios o vectores polares, que no cambian de sentido cuando sé efectúa la transformación de coordenadas antedicha). Por ejemplo, el producto vectorial de dos vectores polares es un seudovector, mientras que el producto vectorial de un seudovector por un vector polar es un vector polar.
La rotación del cuerpo se dice que es uniforme si el valor numérico de su velocidad angular no varía con el tiempo:![]() = const. En este caso el ángulo de rotación del sólido depende linealmente del tiempo:
= const. En este caso el ángulo de rotación del sólido depende linealmente del tiempo:![]()
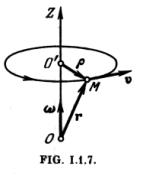
4°. Un punto arbitrario M de un sólido que gira alrededor de un eje fijo OZ con la velocidad angular ![]() , describe una circunferencia de radio p con centro en el punto O’ (fig. 1.1.7). La velocidad v del punto M, a diferencia de la velocidad angular del sólido, se llama frecuentemente velocidad
, describe una circunferencia de radio p con centro en el punto O’ (fig. 1.1.7). La velocidad v del punto M, a diferencia de la velocidad angular del sólido, se llama frecuentemente velocidad
lineal. Esta velocidad tiene dirección perpendicular al eje de rotación (es decir, al vector ![]() ) y al radio vector
) y al radio vector ![]() trazado al punto M desde el centro de la circunferencia O’, e igual a su producto vectorial:
trazado al punto M desde el centro de la circunferencia O’, e igual a su producto vectorial:
![]()
Aquí r = OO’ +![]() es el radio vector del punto M trazado desde el punto O del eje de rotación tomado como origen de coordenadas.
es el radio vector del punto M trazado desde el punto O del eje de rotación tomado como origen de coordenadas.
5°. Se llama período de rotación el intervalo de tiempo T durante el cual el sólido, girando uniformemente con la velocidad (o, da una vuelta completa alrededor del eje de rotación, es decir, gira un ángulo ![]() ):
):![]()
La frecuencia de rotación ![]() indica el número de vueltas (revoluciones) que da el sólido en la unidad de tiempo, cuando la rotación es uniforme y la velocidad angular es
indica el número de vueltas (revoluciones) que da el sólido en la unidad de tiempo, cuando la rotación es uniforme y la velocidad angular es ![]() .
.
6°. El movimiento de un sólido en el cual uno de sus puntos permanece fijo, se denomina rotación del sólido alrededor de un punto fijo. Por lo general, este punto se toma como origen de coordenadas del sistema de referencia en reposo. En la rotación alrededor de un punto fijo todos los puntos del cuerpo se mueven por superficies de esferas concéntricas cuyos centros se hallan en el punto fijo. Este movimiento del sólido se puede considerar en cada instante como rotación alrededor de cierto eje que pasa por el punto fijo y recibe el nombre de eje instantáneo de rotación. En el caso general, la posición del eje instantáneo de rotación varía tanto con respecto a un sistema de referencia fijo, como con respecto a un sistema de referencia solidario del sistema que gira.
La velocidad v de un punto arbitrario M del sólido es:
![]()
Aquí ![]() es la velocidad angular del cuerpo, dirigida a lo largo del eje instantáneo de rotación, lo mismo que el vector
es la velocidad angular del cuerpo, dirigida a lo largo del eje instantáneo de rotación, lo mismo que el vector![]() de la rotación elemental del sólido durante el pequeno tiempo dt; r es el radio vector trazado al punto M desde el punto fijo O, alrededor del cual gira el sólido, y p es la distancia desde el punto M hasta el eje instantáneo de rotación. El sólido, en este caso, puede realizar tres movimientos independientes, a saber: girar alrededor de cada uno de los tres ejes perpendiculares entre sí que pasan por el punto fijo O. Por con siguiente, tiene tres grados de libertad (1.1.2.7°).
de la rotación elemental del sólido durante el pequeno tiempo dt; r es el radio vector trazado al punto M desde el punto fijo O, alrededor del cual gira el sólido, y p es la distancia desde el punto M hasta el eje instantáneo de rotación. El sólido, en este caso, puede realizar tres movimientos independientes, a saber: girar alrededor de cada uno de los tres ejes perpendiculares entre sí que pasan por el punto fijo O. Por con siguiente, tiene tres grados de libertad (1.1.2.7°).
7°. Para caracterizar la rapidez con que varía el vector velocidad angular del sólido durante la rotación no uniforme del cuerpo alrededor de un eje fijo o de un punto fijo, se introduce el vector aceleración angular e del sólido, igual a la primera derivada de su velocidad angular ![]() respecto del tiempo t,
respecto del tiempo t,
![]()
Si el sólido gira alrededor de un eje fijo, el vector e está dirigido a lo largo de este eje, en el mismo sentido que ![]() cuando la rotación es acelerada
cuando la rotación es acelerada![]() , y en sentido contrario si la rotación es retardada
, y en sentido contrario si la rotación es retardada![]() . La proyección de la aceleración angular sobre el eje de rotación fijo OZ es igual a
. La proyección de la aceleración angular sobre el eje de rotación fijo OZ es igual a
![]()
donde ![]() es la proyección sobre este mismo eje del vector
es la proyección sobre este mismo eje del vector ![]() .
.
8°. La aceleración a de un punto arbitrario M del sólido que gira alrededor de un punto fijo O ó de un eje fijo que pasa por dicho punto suele llamarse, para diferenciarla de la aceleración angular del sólido, aceleración lineal. Esta aceleración
![]()
donde![]() es la aceleración circular o de rotación del punto y
es la aceleración circular o de rotación del punto y ![]() es su aceleración axípeta y está dirigida hacia el eje de rotación instantáneo.
es su aceleración axípeta y está dirigida hacia el eje de rotación instantáneo.
Si el sólido gira alrededor de un eje fijo OZ (fig. 1.1.7), la aceleración circular del punto M coincide con su aceleración tangencial![]() (1.1.4.5°), y la aceleración axípeta, con la aceleración normal
(1.1.4.5°), y la aceleración axípeta, con la aceleración normal![]() (1.1.4.6o):
(1.1.4.6o):
![]()
9°. Todo movimiento complejo de un sólido se puede descomponer en dos movimientos simples: uno de traslación, con la velocidad VA de cierto punto arbitrario A del sólido, y otro de rotación alrededor de un eje instantáneo que pase por dicho punto. La velocidad angular![]() no depende del punto A que se elija. La velocidad de un punto arbitrario M del sólido
no depende del punto A que se elija. La velocidad de un punto arbitrario M del sólido
![]()
donde r y rA son, respectivamente, los radios vectores de los puntos M y A.
En la dinámica del sólido suele ser conveniente considerar el movimiento complejo del cuerpo como la composición de dos movimientos simultáneos: uno de traslación con la velocidad del centro de inercia (1.2.3.3°) y otro de rotación alrededor de dicho centro. El caso más simple de movimiento complej o de un sólido es el movimiento plano o planoparalelo, en el cual todos los puntos del sólido se mueven en planos paralelos. Este movimiento lo efectúa, por ejemplo, un cilindro circular homogéneo que ruede por un plano inclinado. En el movimiento plano no varia la dirección del eje instantáneo de rotación del sólido alrededor de punto A, y los vectores ![]() y VA son perpendiculares entre sí.
y VA son perpendiculares entre sí.
