Una lente de vidrio biconvexa, con radios de curvatura de superficies iguales, tiene en el aire una distancia focal 
y en el agua 
. ¿En qué distancia 
y 
de la lente se encontrarán sus focos, cuando esta lente sea colocada en la superficie de separación entre el aire y el agua? El índice de refracción del aire es igual a la unidad y del agua,
.
Solución
Designemos por R el radio de curvatura de las superficies de la lente; por 
, el índice de refracción del vidrio. Entonces
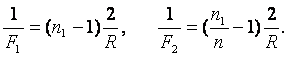
Al mismo tiempo, si la lente se encuentra en la superficie de separación de los medios y los rayos parten del agua, el foco de la lente está situado en el aire, a una distancia , siendo
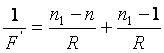
De tal modo, si los rayos parten del aire, el foco se encuentra en el agua a una distancia , siendo
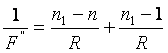
De estas cuatro ecuaciones deducimos
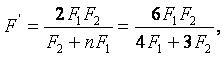
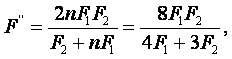
¿Cuál es el radio R de un espejo cóncavo que se encuentra a=2m de la cara de un hombre que ve en el espejo su imagen vez y media mayor que en un espejo plano situado a la misma distancia de la cara del hombre?
Solucion
Basándose en la fórmula del espejo
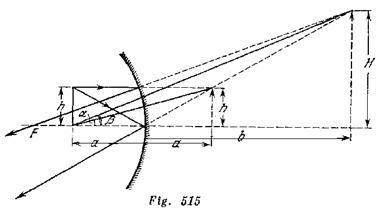
El aumento lineal del espejo es
Las dimensiones angulares de la imagen es un espejo cóncavo, por las condiciones del problema, son 1,5 veces mayores que las dimensiones angulares de la imagen en un espejo plano: 
(fig. 515) es evidente que 
Cuando 
los ángulos 
serán pequeños. Para pequeños ángulos
Excluyendo de las ecuaciones las incógnitas 
. Determinamos que 
. Por consiguiente 
,