En una lente convergente, con distancia focal igual a ![]() , incide un haz de rayos paralelo. ¿Dónde es necesario colocar una lente divergente, con distancia focal igual a
, incide un haz de rayos paralelo. ¿Dónde es necesario colocar una lente divergente, con distancia focal igual a ![]() , para que el haz de rayos, después de pasar por dos lentes, continúe paralelo?
, para que el haz de rayos, después de pasar por dos lentes, continúe paralelo?
Solución
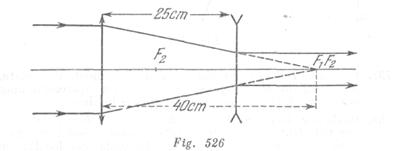
La lente divergente debe colocarse a una distancia de ![]() de la convergente. De este modo, los focos de las lentes divergente y convergente se coincidirán. En la fig. 526 está representado, mediante el gráfico, el recorrido de los rayos.
de la convergente. De este modo, los focos de las lentes divergente y convergente se coincidirán. En la fig. 526 está representado, mediante el gráfico, el recorrido de los rayos.
¿A qué distancia de una lente biconvexa, con distancia focal ![]() , es necesario colocar un espejo esférico cóncavo que tiene un radio, de curvatura
, es necesario colocar un espejo esférico cóncavo que tiene un radio, de curvatura ![]() , para que el rayo que incide en la lente paralelamente al eje óptico principal del sistema, después de reflejarse en el espejo, salga de la lente y continúe paralelo al eje óptico? Encontrar las imágenes de un objeto proyectadas por este sistema óptico.
, para que el rayo que incide en la lente paralelamente al eje óptico principal del sistema, después de reflejarse en el espejo, salga de la lente y continúe paralelo al eje óptico? Encontrar las imágenes de un objeto proyectadas por este sistema óptico.
Solucion
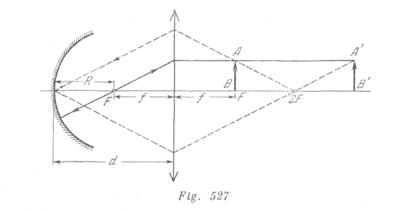
1).El espejo se encuentra a una distancia ![]() de la lente. El trayecto del rayo, paralelo al eje óptico del sistema, así como la imagen del objeto AB, se dan en la fig. 527. La imagen A’B’ (directa y real) se obtiene en el tamaño natural para cualquier posición del objeto.
de la lente. El trayecto del rayo, paralelo al eje óptico del sistema, así como la imagen del objeto AB, se dan en la fig. 527. La imagen A’B’ (directa y real) se obtiene en el tamaño natural para cualquier posición del objeto.
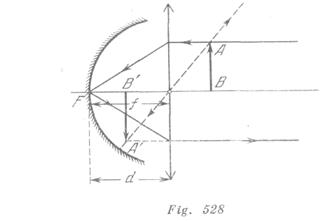
2).El espejo se encuentra a una distancia ![]() de la lente (fig. 528). La imagen del objeto A’B tendrá también un tamaño natural, siendo inversa y virtual para cualquier posición del objeto.
de la lente (fig. 528). La imagen del objeto A’B tendrá también un tamaño natural, siendo inversa y virtual para cualquier posición del objeto.
Un sistema óptico consta de dos lentes convergentes con distancias focales ![]() y
y ![]() . La distancia entre las lentes es
. La distancia entre las lentes es ![]() . El objeto se encuentra a una distancia
. El objeto se encuentra a una distancia ![]() de la primera lente. ¿A qué distancia de la segunda se obtendrá la imagen?
de la primera lente. ¿A qué distancia de la segunda se obtendrá la imagen?
Solucion
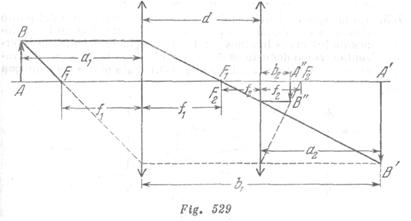
El trayecto de los rayos en el sistema óptico dado está representado en la fig. 529. La primera lente, en la ausencia de la segunda, crea la imagen A’B’ que se encuentra a una distancia ![]() de la lente. Esta distancia se halla por la fórmula de la lente:
de la lente. Esta distancia se halla por la fórmula de la lente:
![]()
La imagen A’B’ es «virtual» con relación a la segunda lente. Por consiguiente,
![]()
donde ![]() de Donde
de Donde ![]()
Determinar la distancia focal de un sistema óptico, constituido por dos lentes delgadas: la una divergente con distancia focal f1 y la otra convergente con distancia focal f2. Las lentes están situadas muy cerca una de la otra. Los ejes ópticos de las lentes coinciden.
Solucion
De la solución del problema anterior se deduce que en el caso de dos lentes convergentes que se encuentran a cierta distancia d la una de la otra es válida la igualdad
![]()
En nuestro caso la lente divergente se encuentra muy cerca de la convergente (d = 0), por eso
![]()
donde f es la distancia focal del sistema que buscamos. De donde ![]()
Dos lentes divergentes iguales están colocadas en el mismo eje de tal modo, que el foco anterior de una y e] foco posterior de 1a otra, están situados en el mismo
punto A del eje. La tercera lente se coloca en este mismo eje para que su centro óptico se encuentre en el punto A. La distancia focal de la tercera lente es tal, que el sistema produce la imagen real de cualquier objeto situado fuera del sistema, pero en su eje. ¿Qué aumento dará el sistema, cuando la distancia entre el objeto y su imagen es la mínima?
Solucion
La lente media (la tercera) es convergente. Si la distancia desde el objeto hasta la lente anterior del sistema es d, entonces la distancia desde la lente posterior hasta la imagen es ![]() , donde F es la distancia focal de la lente divergente. El aumento del sistema es
, donde F es la distancia focal de la lente divergente. El aumento del sistema es ![]() . A distancia mínima entre el objeto y su imagen (esta distancia es 3F)
. A distancia mínima entre el objeto y su imagen (esta distancia es 3F) ![]() .
.
Un haz paralelo de luz cae en un sistema de tres lentes delgadas con el eje óptico común. Las distancias focales de las lentes son iguales a ![]() ,
, ![]() y
y ![]() , respectivamente. La distancia entre la primera y la segunda lentes es
, respectivamente. La distancia entre la primera y la segunda lentes es ![]() , entre la segunda y la tercera es
, entre la segunda y la tercera es ![]() . Determinar la posición del punto de convergencia del haz al salir del sistema de las lentes.
. Determinar la posición del punto de convergencia del haz al salir del sistema de las lentes.
Solucion
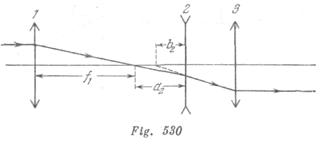
En la segunda lente incide un haz luminoso que sale del punto situado a una distancia ![]() de la lente. Las prolongaciones de los rayos luminosos refractados por esta lente, se interceptan, como deducimos de la fórmula de la lente a una distancia
de la lente. Las prolongaciones de los rayos luminosos refractados por esta lente, se interceptan, como deducimos de la fórmula de la lente a una distancia ![]() de la misma (fig.530). Este punto coincide con el foco de la tercera lente. Por eso, los rayos que salen del sistema, formarán un haz de rayos paralelos. El sistema dado es telescópico.
de la misma (fig.530). Este punto coincide con el foco de la tercera lente. Por eso, los rayos que salen del sistema, formarán un haz de rayos paralelos. El sistema dado es telescópico.
Cierto sistema óptico proyecta la imagen real de una fuente en un punto A. La dimensión de la imagen es 1mm. Otro sistema óptico consta de dos lentes convergentes, situadas de modo, que el centro de la una coincide con el foco de la otra e inversamente. El segundo sistema se coloca en el mismo eje que el primero de tal modo, que el punto A se encuentre entre las lentes, aproximadamente en el medio. Hallar la dimensión de la imagen proyectada por el segundo sistema.
Solucion
La imagen obtenida por el segundo sistema es virtual. Ella se encuentra en el plano focal anterior de la primera lente. El tamaño de la imagen es igual a 2mm.
Un sistema óptico consta de dos lentes con distancias focales iguales en magnitud absoluta. Una de las lentes es convergente y la otra es divergente. Las lentes están instaladas en el mismo eje, a cierta distancia la una de la otra. Se sabe que al cambiar las lentes, la imagen real de la Luna, proyectada por el sistema, se desplaza en ![]() . Encontrar la distancia focal de cada una de las lentes.
. Encontrar la distancia focal de cada una de las lentes.
Solucion
Supongamos que la distancia entre las lentes sea a. Entonces, si los rayos caen primero sobre la lente divergente, la ecuación para la segunda (convergente) lente se escribirá en la siguiente forma:
![]()
En el caso cuando en el primer plano se encuentra la lente convergente, la ecuación para la lente divergente se escribirá del siguiente modo:
![]()
donde f1 y f2 son las distancias desde la lente posterior hasta la imagen en el primer y en el segundo casos. Por la condición tenemos ![]() . De estas igualdades recibimos
. De estas igualdades recibimos ![]() .
.
¿Cuál deberá ser la distancia focal Fx de una lente convergente que proyecte una imagen de la Luna, igual, en magnitud, a la imagen proyectada por el
sistema de dos lentes mencionado en el problema 767? La distancia entre las lentes es ![]() .
.
Solucion
El diámetro de la imagen de la Luna obtenida con ayuda de una lente es ![]() , donde j es el diámetro angular de la Luna. El diámetro de la imagen real, producido por el sistema dado, es
, donde j es el diámetro angular de la Luna. El diámetro de la imagen real, producido por el sistema dado, es ![]() , donde a es la distancia entre las lentes; su distancia focal (véase la resolución del problema 767). Por consiguiente,
, donde a es la distancia entre las lentes; su distancia focal (véase la resolución del problema 767). Por consiguiente,![]() .
.
¿Para qué posición (una de las dos) de las lentes, indicadas en el problema 767, las dimensiones de la imagen real de la Luna serán mayores?
Solucion
La dimensión de la imagen formada por la primera lente no depende del tipo de la lente: si es divergente o convergente. En ambos casos el diámetro de la imagen es igual a jF, donde j es el diámetro angular de la Luna. Si la segunda lente es convergente, su aumento es ![]() . Del modo análogo, si la segunda lente es divergente, entonces
. Del modo análogo, si la segunda lente es divergente, entonces ![]() , de donde se deduce que k1 = k2 y el diámetro de la imagen definitiva
, de donde se deduce que k1 = k2 y el diámetro de la imagen definitiva ![]() es igual en ambos casos.
es igual en ambos casos.
Una lente con distancia focal ![]() proyecta en una pantalla la imagen nítida de un objeto situado a una distancia
proyecta en una pantalla la imagen nítida de un objeto situado a una distancia ![]() de la lente. Entre la lente y el objeto, perpendicularmente al eje óptico de la lente, fue colocada una lámina plano-paralela, de espesor
de la lente. Entre la lente y el objeto, perpendicularmente al eje óptico de la lente, fue colocada una lámina plano-paralela, de espesor ![]() . ¿A qué distancia es necesario desplazar la pantalla para que la imagen del objeto continúe nítida? El índice de refracción del vidrio de la lámina es
. ¿A qué distancia es necesario desplazar la pantalla para que la imagen del objeto continúe nítida? El índice de refracción del vidrio de la lámina es ![]()
Solucion
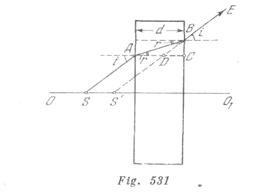
En la fig. 531 se muestra el trayecto del rayo a través de la lámina del punto S del objeto. Como resultado de la refracción de la luz en la lámina, tenemos la impresión que el rayo BE sale del punto S’; S’ es la imagen virtual de S sobre la lamina.
De este modo la distancia entre la imagen del objeto en la lámina y la lente es ![]() . El desplazamiento
. El desplazamiento ![]() . Considerando los ángulos de incidencia sobre la lámina pequeños, tendremos
. Considerando los ángulos de incidencia sobre la lámina pequeños, tendremos
![]()
ya que ![]() . Por consiguiente,
. Por consiguiente, ![]() . Hasta el momento de colocar la lámina, la pantalla se encontraba a una distancia
. Hasta el momento de colocar la lámina, la pantalla se encontraba a una distancia ![]() ; después de colocarla, la pantalla se encontrará a una distancia
; después de colocarla, la pantalla se encontrará a una distancia ![]() . Entonces es necesario mover la pantalla en
. Entonces es necesario mover la pantalla en![]() .
.
Un objeto AB se encuentra a una distancia ![]() de una lente con distancia focal
de una lente con distancia focal ![]() . A una distancia
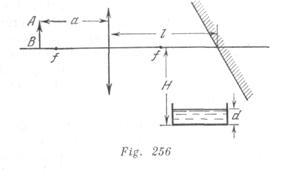
. A una distancia ![]() , detrás de la lente está instalado un espejo plano, inclinado en 45° con relación al eje óptico (fig. 256). ¿A qué distancia H del eje óptico es necesario colocar el fondo de una cubeta con agua para obtener en él una imagen nítida del objeto? La profundidad del agua en la cubeta es
, detrás de la lente está instalado un espejo plano, inclinado en 45° con relación al eje óptico (fig. 256). ¿A qué distancia H del eje óptico es necesario colocar el fondo de una cubeta con agua para obtener en él una imagen nítida del objeto? La profundidad del agua en la cubeta es ![]() .
.
Solucion
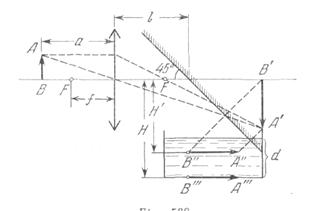
Sin el espejo la imagen del objeto A ‘B’ se produce a una distancia ![]() de la lente (fig. 532). Después de reflejarse en el espejo la imagen ocupará una posición A”B” y se encontrará a una distancia
de la lente (fig. 532). Después de reflejarse en el espejo la imagen ocupará una posición A”B” y se encontrará a una distancia ![]() del eje óptico. La capa del agua de espesor d desplazará la imagen en una distancia
del eje óptico. La capa del agua de espesor d desplazará la imagen en una distancia ![]() , donde n es el índice de refracción del agua. Esto se deduce directamente de la resolución del problema 770. Por consiguiente,
, donde n es el índice de refracción del agua. Esto se deduce directamente de la resolución del problema 770. Por consiguiente, ![]() .
.
Una cuña de vidrio, con pequeño ángulo de refracción α, fue colocada a cierta distancia de una lente convergente con distancia focal f, siendo una de las superficies de la cuña perpendicular al eje óptico de la lente. Al otro lado de la lente, en su foco se encuentra una fuente luminosa puntual. Los rayos reflejados por la cuña proyectan, después de reflejarse en la lente, dos imágenes de la fuente, desplazadas la una relativamente de la otra, a una distancia d. Encontrar el índice de refracción del vidrio de la cuña.
Solucion
Serán posibles dos casos:
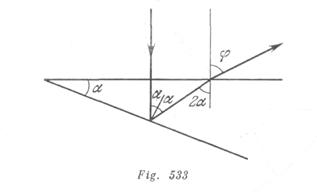
1) El eje óptico de la lente es perpendicular a la cara anterior de la cuña. Los rayos reflejados de la cara anterior, pasando por la lente crean una imagen de la fuente puntual que coincide con la propia fuente. Los rayos reflejados de la cara posterior se inclinan bajo un ángulo j (fig. 533) que se determina por la igualdad: ![]() . Debido a la pequeña dimensión de los ángulos resulta que
. Debido a la pequeña dimensión de los ángulos resulta que ![]() . La segunda imagen de la fuente se producirá a una distancia d de la primera imagen:
. La segunda imagen de la fuente se producirá a una distancia d de la primera imagen:
![]() . donde
. donde ![]()
2)
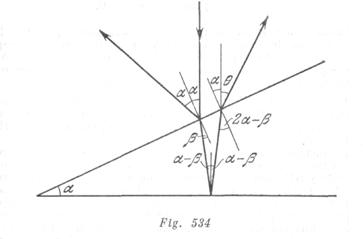
El eje óptico de la lente es perpendicular a la superficie posterior de la cuña. Los rayos reflejados de la superficie anterior se inclinan bajo un ángulo y = 2 a y crean una imagen que se encuentra de la fuente a una distancia ![]() (fig. 534).
(fig. 534).
Los rayos reflejados de la superficie posterior se inclinan bajo un ángulo q determinado de las ecuaciones sen
![]() ,
, ![]()
Cuando los ángulos son pequeños,![]() .Por eso la segunda imagen se encontrará a una distancia
.Por eso la segunda imagen se encontrará a una distancia ![]() de la fuente. La distancia total entre las imágenes será
de la fuente. La distancia total entre las imágenes será ![]() , de donde
, de donde ![]() , como en el caso (1).
, como en el caso (1).
En el espejo cóncavo que tiene la forma de una semiesfera de radio ![]() , se vierte una capa fina de un líquido desconocido transparente. Gracias a ello, se tiene la impresión de que tal sistema óptico, en determinada posición de la fuente, proyecta dos imágenes reales, una de las cuales coincide con la propia fuente y la otra está de la fuente a una distancia
, se vierte una capa fina de un líquido desconocido transparente. Gracias a ello, se tiene la impresión de que tal sistema óptico, en determinada posición de la fuente, proyecta dos imágenes reales, una de las cuales coincide con la propia fuente y la otra está de la fuente a una distancia ![]() . Hallar el índice de refracción n del líquido.
. Hallar el índice de refracción n del líquido.
Solucion
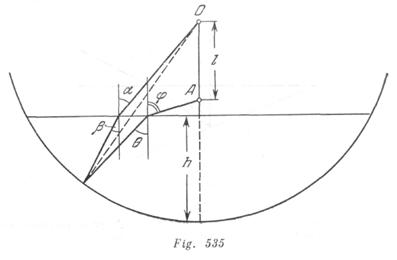
Como la imagen que coincide con la fuente se forma como consecuencia de la reflexión de la parte del espejo no cubierta por el líquido, es evidente que la fuente se sitúa en el centro de la semiesfera O. Determinemos la posición de otra imagen (punto A en la fig. 535). De acuerdo con la ley de la refracción
![]()
Como vemos en el dibujo ![]() , donde
, donde ![]() es el ángulo de incidencia del rayo refractado sobre el espejo y
es el ángulo de incidencia del rayo refractado sobre el espejo y ![]() . Prescindiendo de h en comparación con R, hallamos del sistema de ecuaciones obtenido, que
. Prescindiendo de h en comparación con R, hallamos del sistema de ecuaciones obtenido, que ![]()
Una lente biconvexa tiene una distancia focal ![]() . Una de las superficies de la lente que tiene el radio de curvatura
. Una de las superficies de la lente que tiene el radio de curvatura ![]() , está cubierta de plata. Construir gráficamente la imagen de un objeto proyectada por este sistema óptico y encontrar la posición de la imagen, conociendo que el objeto está a una distancia
, está cubierta de plata. Construir gráficamente la imagen de un objeto proyectada por este sistema óptico y encontrar la posición de la imagen, conociendo que el objeto está a una distancia ![]() de la lente.
de la lente.
Solucion
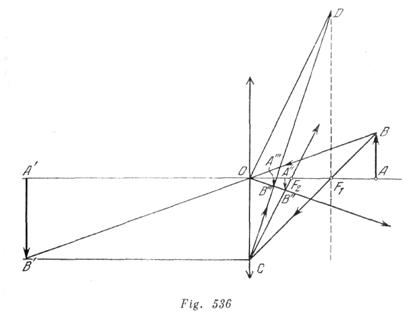
La imagen A”’B”’ obtenida en el sistema, se muestra en la fig. 536. F1 y F2 son los focos de la lente y del espejo; A’B’ es la imagen proyectada por la lente en el caso, cuando su superficie no está plateada. La imagen A “B” producida por el espejo cóncavo, puede construirse, conociendo que el rayo BO, después de pasar por la lente y reflejarse de la superficie del espejo, seguirá el trayecto OB”, siendo ÐBOA = ÐB”OA. El rayo BC sale de la lente paralelamente al eje óptico del sistema y después de reflexión pasará por F2. Los rayos reflejados del espejo se refractan en la lente una vez más y producen la imagen A”‘B”‘. El punto B´´´ se encuentra en la intersección de los rayos OB” y CD. El rayo OB” después de reflexión pasa por el centro óptico de la lente y por eso no se refracta. El rayo CD se construye del siguiente modo. Después de la primera refracción en la lente y de la reflexión, el rayo BC seguirá en dirección de F2 y se refractara en la lente una vez más. Su dirección, después de la segunda refracción, se halla mediante el método utilizado en el problema 753: a través del centro óptico 0 hasta la intersección con el plano focal de la lente se traza el rayo 0D, paralelo a CF2. Entonces, uniendo C y D obtenernos el rayo incógnito.
Como los rayos se refractan en la lente dos veces, la distancia focal f del sistema puede determinarse de la relación (véase el problema 763):
![]()
Donde ![]() es la distancia focal del espejo. De este modo,
es la distancia focal del espejo. De este modo,![]() .De donde la distancia b hasta la imagen A”‘B”‘ se encuentra por la fórmula
.De donde la distancia b hasta la imagen A”‘B”‘ se encuentra por la fórmula
![]()
Por lo tanto![]()
Una lente plano-convexa de vidrio (el índice de refracción es n) con un lado plano plateado tiene distancia focal F1. ¿Qué distancia focal tendrá esta lente, si plateamos el lado convexo y no el plano?
Solucion
La convergencia del sistema es igual a la suma de las convergencias de sus componentes (si ellas se encuentran juntas).
En el primer caso,
![]()
En el segundo caso,
![]()
de donde ![]() .
.
